5. 抵抗の直並列接続

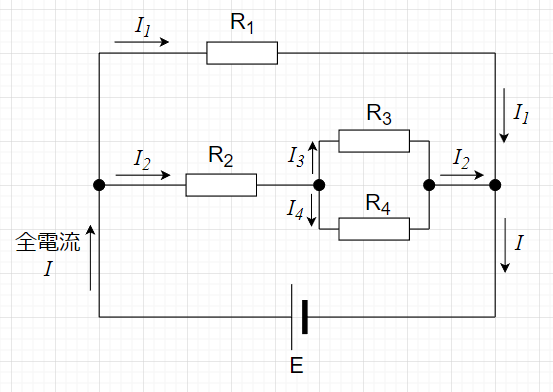
図「直並列接続回路」で\(R_3\)と\(R_4\)は並列接続で$$R_p =\frac{R_3 R_4}{R_3 + R_4}$$となる。\(R_2\)と\(R_p\)は直列接続なので、$$R_b = R_2 + R_p$$となる。さらに、\(R_1\)と\(R_b\)は並列接続なので、全体の合成抵抗は、$$R_T = \frac{R_1 R_b}{R_1+ R_b}$$となる。以上より、全電流は$$I = \frac{E}{R_T}$$となる。分流の式より、$$I_1 = \frac{R_b}{R_1 + R_b} I \;\;\; , \;\;\; I_2 = \frac{R_1}{R_1 + R_b} I$$ となる。\(R_1\)による電圧降下\(V_1\)と、\(R_b\)による電圧降下\(V_b\)は、$$V_1 = R_1 I_1 \;\;\;, \;\;\; V_b = R_b I_2$$となる。また、\(R_3 \;,\;R_4\)に流れる電流は、$$I_3 = \frac{R_4}{R_3 + R_4} I_2 \;\;\; ,\;\;\; I_4 = \frac{R_3}{R_3 + R_4} I_2$$である。\(R_3\)による電圧降下\(V_3\)と、\(R_4\)による電圧降下\(V_4\)は、$$V_3 = R_3 I_3 \;\;\;, \;\;\; V_4 = R_4 I_4$$となる。電流の関係は、$$I_2 = I_3 + I_4 \;\;\; ,\;\;\; I = I_1 + I_2$$である。

※全抵抗\(R_T\)の式を上式を組み合わせて、\(R_1 , R_2, R_3 , R_4\)で表すことも可能であるが、実用的には必要性は低いし、簡単なプログラムで求められるので、各式の関係を整理できれば十分である。さらに、実用上は回路図CAD＆シミュレータで各部の電流、電圧は求められので、原理が理解できていれば良いだろう。