21. システムの特性表現

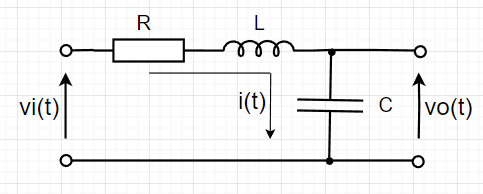
R：抵抗、　L：インダクタ―（コイル）、　
C：キャパシタ―（コンデンサー）

微分方程式

RLC回路において、入力電圧を\(v_i(t)\) 、出力電圧を\(v_o(t)\)として微分方程式で表すと、
$$v_i(t)=Ri(t)+L\frac{di(t)}{dt} +v_o(t)$$ $$v_o(t)=\frac{1}{C}\int i(t)dt$$ $$i(t)=C\frac{dv_o(t)}{dt}　,　\frac{di(t)}{dt}=C\frac{d^2v_o(t)}{dt^2}$$ $$v_i(t)=RC\frac{dv_o(t)}{dt} + LC\frac{d^2v_o(t)}{dt^2} + v_o(t)　（A）$$となる。この数式で表したモデルがシステム解析の基本となる。

伝達関数

微分方程式（A)を初期値０でラプラス変換すると、$$V_i(s)=RCsV_o(s)+LCs^2V_o(s)+V_o(s)$$ $$V_i(s)=(LCs^2+RCs+1)V_o(s)$$となる。よって、伝達関数は、 $$G(s)=\frac{V_o(s)}{V_i(s)}=\frac{1}{LCs^2+RCs+1}$$ $$=\frac{\frac{1}{LC}}{s^2 + \frac{R}{L} s+ \frac{1}{LC}}$$と表せる。ここで、\(\omega_n^2=\frac{1}{LC}\) 、\(2\zeta \omega_n=\frac{R}{L}\)として、
固有角周波数：\(\omega_n=\frac{1}{\sqrt{LC}}\)　、　減衰係数：\(\zeta=\frac{R}{2}\sqrt{\frac{C}{L}}\) 　とすると、$$G(s)=\frac{\omega_n^2}{s^2 + 2\zeta \omega_n s+ \omega_n^2} $$標準2次系の伝達関数で表せる。

インパルス応答

単位インパルス信号\(\delta (t)\)のラプラス変換は、\(\mathcal{L}\left\{\delta(t)\right\}=1\)なので、インパルス応答\(g(t)\)は、$$g(t)=\mathcal{L}^{-1}\left\{G(s)\cdot 1\right\}=\mathcal{L}^{-1}\left\{G(s)\right\}$$すなわち、伝達関数の逆ラプラス変換で求まる。
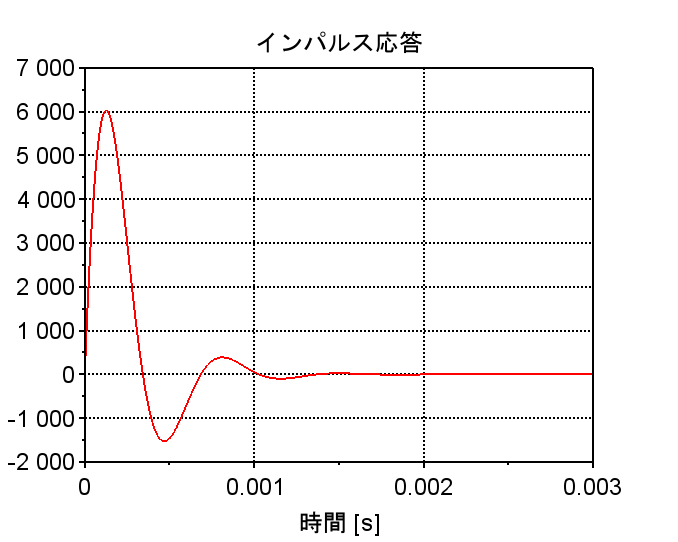
R=8［Ω］、L=1［mH]、C=10［μF]とすると\(\omega_n=10000\) [rad/s] 　,　\(\zeta= 0.4\)　となる。このときのインパルス応答は、以下の図のようになる。
インパルス応答が\(t \rightarrow \infty\)で、\(g(t) \rightarrow 0\)なので、安定であるが、若干振動的であるので、電気回路としては電源投入時などの初動に気を付けなければいけない場合があることが想定される。

ステップ応答

単位ステップ信号\(I (t)\)のラプラス変換は、\(\mathcal{L}\left\{I(t)\right\}=\frac{1}{s}\)なので、ステップ応答\(y(t)\)は、$$y(t)=\mathcal{L}^{-1}\left\{G(s)\cdot \frac{1}{s}\right\}$$で求まる。
R=8［Ω］、L=1［mH]、C=10［μF]とすると\(\omega_n=10000\) [rad/s] 　,　\(\zeta= 0.4\)　となる。このときステップ応答は、以下の図のようになる。

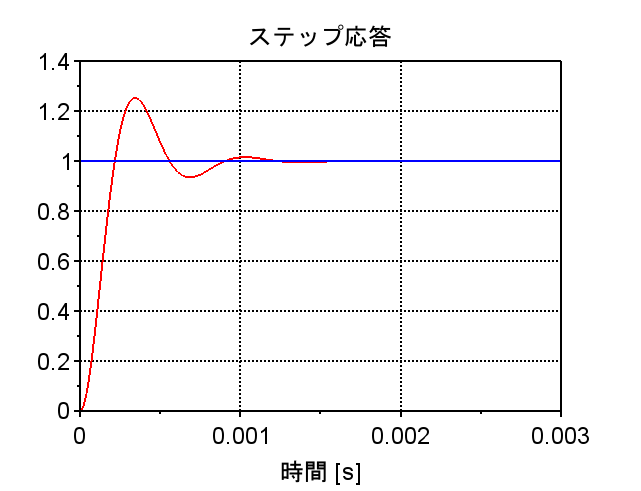
ボード線図

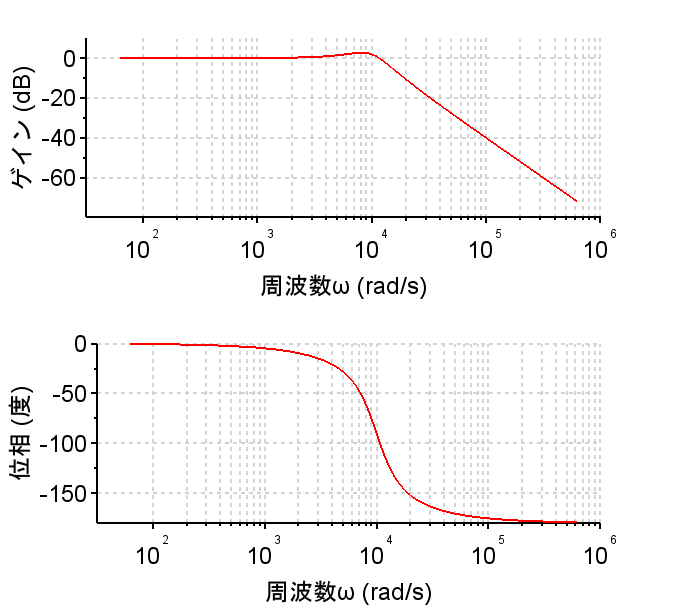
伝達関数\(G(s)\)で、\(s \rightarrow j\omega \)とすることで、周波数伝達関数 \(G(j \omega) \)が求まる。$$G(j \omega)=\left|G(j \omega)\right| e^{j \phi(\omega)} 　,　\phi(\omega)=\arg G(j \omega)$$LCR回路では、$$G(j \omega)=\frac{\frac{1}{LC}}{(j \omega)^2 + \frac{R}{L}(j \omega) + \frac{1}{LC}}$$ R=8［Ω］、L=1［mH]、C=10［μF]とすると　$$G(j \omega)=\frac{10^8}{10^8 -\omega^2 + j8000\omega}$$となる。これより、ゲイン、位相を求めボード線図で表す。図の作成にはScilabなどのソフトウェアを利用するとよい。

ベクトル軌跡

周波数伝達関数 \(G(j \omega) \)は、$$G(j \omega)=\left|G(j \omega)\right| e^{j \phi(\omega)} 　,　\phi(\omega)=\arg G(j \omega)$$なので、原点からの距離が\(\left|G(j \omega)\right|\)、実軸との角度が \(\arg G(j \omega)\)のベクトルで表せる。角周波数\(\omega\)を\(0 \rightarrow \infty\)と変化させたときのベクトルの先端の軌跡を描いたものがベクトル軌跡となる。

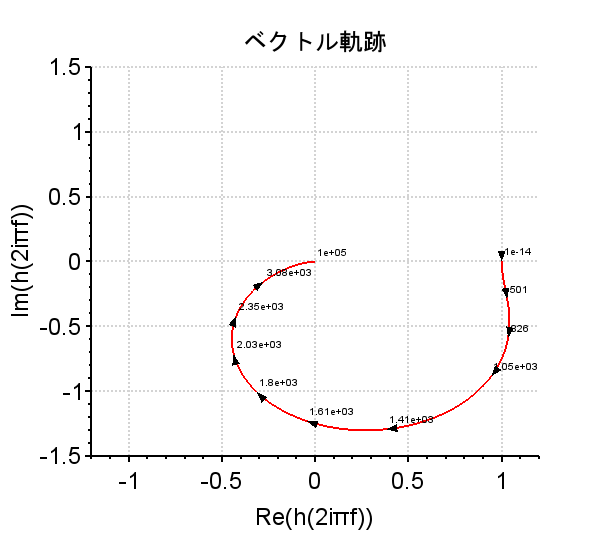
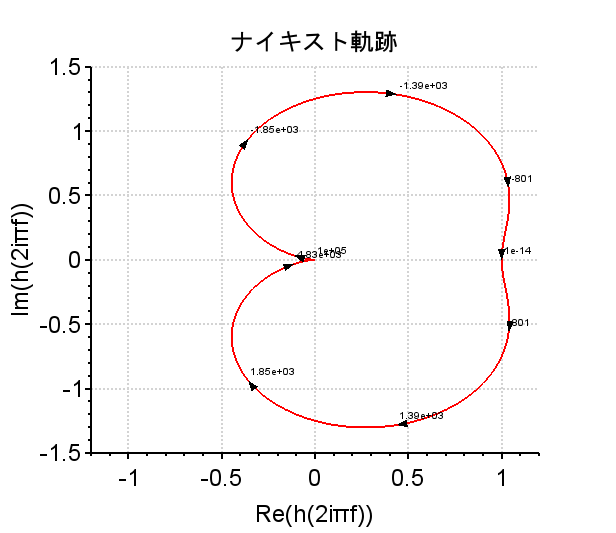
ナイキスト軌跡

周波数伝達関数 \(G(j \omega) \)は、$$G(j \omega)=\left|G(j \omega)\right| e^{j \phi(\omega)} , \phi(\omega)=\arg G(j \omega)$$なので、原点からの距離が\(\left|G(j \omega)\right|\)、実軸との角度が \(\arg G(j \omega)\)のベクトルで表せる。角周波数\(\omega\)を\(-\infty \rightarrow +\infty\)と変化させたときのベクトルの先端の軌跡を描いたものがナイキスト軌跡となる。