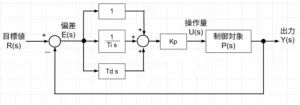
13-1. オブザーバ併合型状態フィードバックによるデッドビート制御
デッドビート制御(有限時間整定制御)は、離散時間システム特有の制御手法で、「サンプリング周期の整数倍という有限の時間内に、状態誤差を完全にゼロにする」という強力な応答特性を持つ制御である。ここでは、これを状態観測器(オブザーバ)を用いた状態フィードバックで実現する方法を考える。
デッドビート制御の原理
※デッドビート制御の基本は、13. デッドビート制御 を参照してください。
連続時間システムでは応答を速くしても偏差を完全にゼロにするには無限の時間がかかる。これに対して、離散時間システムでは閉ループ系のすべての極を\(Z\)平面の原点 (\(z=0\)) に配置することで、有限スッテプ数での整定が可能になる。
・特性方程式: \(\text{det}(zI - (A-bf)) = z^n = 0\)(\(n\)はシステムの次数)このとき、状態遷移行列\((A- bf)^n\)は零行列となり、いかなる初期状態からも最大 \(n\)ステップで状態が原点に到達する。
状態フィードバックによるデッドビート
すべての状態が直接観測できると仮定した場合、制御入力\(u(k) = -Fx(k)\)を用いる。状態方程式は\(x(k+1) = (A - BF)x(k)\)となる。デッドビート制御の設計目標は行列\(A - BF\)のすべての固有値が\(0\)になるようにフィードバックゲイン\(F\)を決定することである。その結果、\(x(k)\)は最大\(n\)ステップで\(0\)に収束する。
状態観測器によるデッドビート
※状態観測器の基本については、14. 状態観測器 を参照してください。
現実的にはすべての状態量を測ることはできないため、状態観測器(オブザーバ)を用いて状態を推定する。状態観測器自体もデッドビート特性を持つように設計できる。
状態観測器の式は\(\hat{x}(k+1) = A\hat{x}(k) + Bu(k) + G(y(k) - C\hat{x}(k))\)と表せる。このとき、推定誤差は\(e(k) = x(k) - \hat{x}(k)\)となる。設計目標は行列 \(A - GC\)のすべての固有値が\(0\)になるようにオブザーバゲイン\(G\) を決定することである。その結果、推定値\(\hat{x}(k)\)は最大\(n\)ステップで真の状態量\(x\)と一致する。
併合系(状態観測器+状態フィードバック)の動作
観測器で推定した状態を使ってフィードバックをかける場合(\(u(k) = -F\hat{x}(k)\))、分離定理により、全体の特性多項式は以下の積になる。$$\text{det}(zI - (A - BF)) \cdot \text{det}(zI - (A - GC)) = z^n \cdot z^n = z^{2n}$$整定までのステップ数は、最初の\(n\)ステップで状態観測器が真の状態量を推定し(推定誤差\(e \to 0\))、次の\(n\)ステップで正確な推定値に基づいたフィードバックにより、状態量が原点に収束する(状態量\(x \to 0\))。したがって、最大\(2n\)ステップ以内にシステム全体が完全に整定する。
アッカーマンの公式によるゲイン設計
デッドビート制御は「すべての閉ループ極を\(z=0\)に配置する」設計で、このとき、ゲイン\(F\)(フィードバック)と\(G\)(オブザーバ)は以下の手順で求める。
・状態フィードバックゲイン\(F\)の算出
システムの可制御性行列を\(W = [B, AB, \dots, A^{n-1}B]\)とすると、$$F = [0, 0, \dots, 1] W^{-1} A^n$$である。※ 通常の極配置では \(A^n\)の部分が特性多項式\(\phi(A)\)になるが、デッドビート(全極\(0\))の場合は\(\phi(z)=z^n\)なので、\(A^n\)を用いる。
・オブザーバゲイン\(G\)の算出
システムの可観測性行列を\(V = [C^T, A^T C^T, \dots, (A^{n-1})^T C^T]^T\)とすると、$$G = A^n V^{-1} [0, 0, \dots, 1]^T$$である。
状態観測器を用いたデッドビート制御は、「まず\(n\)ステップで状況を把握し、次の\(n\)ステップで目標に収束させる」という、ディジタル制御における最短攻略法である。しかし、実用的には、操作量の飽和の問題なをを避けるために、極を原点から少し散らす「ソフトなデッドビート」に近い設計が行われることが多い。
2次系システムでの例
式(1)の簡単な離散時間システムを例に、デッドビート制御器を設計する。
$$A = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, \quad B = \begin{bmatrix} 0.5 \\ 1 \end{bmatrix}, \quad C = \begin{bmatrix} 1 & 0 \end{bmatrix}$$ (このシステムは、サンプリング周期\(T=1\)で等速直線運動する物体をモデル化したものである。状態量\(x1\):位置、\(x2\):速度である。)
・フィードバックゲイン\(F\)の計算
可制御性行列:$$W = [B \quad AB] = \begin{bmatrix} 0.5 & 1.5 \\ 1 & 1 \end{bmatrix}$$逆行列:$$W^{-1} = \begin{bmatrix} -1 & 1.5 \\ 1 & -0.5 \end{bmatrix}$$\(A^2\)の計算:$$A^2 = \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix}$$アッカーマンの公式適用:$$F = [0 \quad 1] \begin{bmatrix} -1 & 1.5 \\ 1 & -0.5 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix} = [1 \quad -0.5] \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix} = [1 \quad 1.5]$$以上より、この\(F = [1 \quad 1.5]\)を使えば、状態がわかっている時に 2ステップ で原点に収束する。
・オブザーバゲイン\(G\)の計算
可観測性行列:$$V = \begin{bmatrix} C \\ CA \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix}$$逆行列 :$$V^{-1} = \begin{bmatrix} 1 & 0 \\ -1 & 1 \end{bmatrix}$$アッカーマンの公式適用:$$G = A^2 V^{-1} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}$$以上より、この\(G = [2, 1]^T\)を使えば、推定値は 2ステップ で真の値に一致する。
※実装上の注意点として、以下が挙げられる。
・サンプリング周期の選択:サンプリング周期\(T\)が短すぎると、アッカーマンの公式で求まるゲイン\(F, G\) が大きな値になり、演算の桁落ちやアクチュエータの飽和(操作量の飽和など)を招く。
・ロバスト性の欠如:デッドビートは「モデルが完璧であること」を前提としている。もし現実の物体の質量が計算より\(10\%\)重かったりすると、有限時間で止まらず、逆に激しく振動することがある。
・対策:実用上は、極を\(0\)に配置せず、原点の近くに少し散らして配置することで、応答の速さを維持しつつ、ノイズや誤差に対する強さ(ロバスト性)を持たせるのが一般的である。
Scilabによるシミュレーション
// デッドビート制御(状態フィードバック+状態観測器)シミュレーション
clear; clc; clf;
// システム行列の定義
A = [1, 1; 0, 1];
B = [0.5; 1];
C = [1, 0];
// 設計したゲイン(アッカーマンの公式より算出)
F = [1, 1.5]; // フィードバックゲイン
G = [2; 1]; // オブザーバゲイン
// シミュレーション設定
N = 10; // シミュレーションステップ数
x = zeros(2, N+1); // 真の状態 [位置; 速度]
x_hat = zeros(2, N+1); // 推定された状態
u = zeros(1, N); // 入力
// 初期値の設定
x(:,1) = [2; -1]; // 真の初期状態(位置2, 速度-1)
x_hat(:,1) = [0; 0]; // 観測器の初期値(ゼロから開始)
// シミュレーションループ(離散時間)
for k = 1:N
// 出力(観測値)の取得
y = C * x(:,k);
// 制御入力の計算(推定値に基づくフィードバック)
u(k) = -F * x_hat(:,k);
// システムの状態更新(真の値)
x(:,k+1) = A * x(:,k) + B * u(k);
// 状態観測器の更新
x_hat(:,k+1) = A * x_hat(:,k) + B * u(k) + G * (y - C * x_hat(:,k));
end
// 結果のプロット
t = 0:N;
subplot(2,1,1);
plot(t, x(1,:), 'b-o', t, x_hat(1,:), 'r--x');
xgrid();
ylabel('Position (x1)');
legend(['True State'; 'Estimated State']);
title('Deadbeat Control Simulation');
subplot(2,1,2);
plot(t, x(2,:), 'b-o', t, x_hat(2,:), 'r--x');
xgrid();
xlabel('Steps (k)');
ylabel('Velocity (x2)');
legend(['True State'; 'Estimated State']);
printf("k=4時点の状態 x1: %e, x2: %e\n", x(1,5), x(2,5));
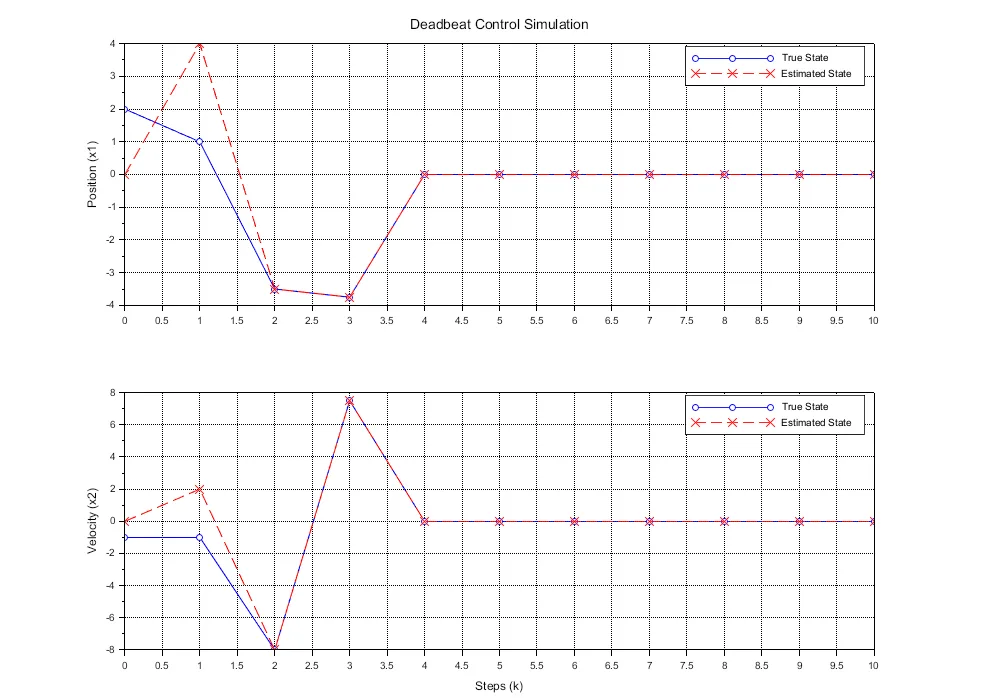
図1のシミュレーション結果は、次のように解釈できる。
\(k=0\): 制御開始。初期状態量\(x(0)\)と推定状態量\(\hat{x}(0)\)の乖離がある。
\(k=1\): オブザーバが情報を収集中。
\(k=2\): 【観測完了】 推定状態量が真の状態量に一致 (\(\hat{x} = x\))。ここから正しい状態フィードバックを開始。
\(k=3\): 状態が原点へ向かって急速に減少。
\(k=4\): 【整定完了】 状態量 \(x\)も誤差\(e\)も完全に\(0\)になる。
このように、\(2n = 4\) ステップで完全に動きが止まる。
モデル誤差がある場合のデッドビート制御
物理モデル(行列Aの成分など)が少しズレていたらどうなるかをシミュレーションで確認する。以下のスクリプトでは、実際のシステムの慣性(行列\(A\)の成分)が設計時より\(5\%\)増加、また、入力ゲインも\(10\%\)ズレたと仮定している状況をシミュレートする。
// モデル誤差がある場合のデッドビート制御シミュレーション
clear; clc; clf;
// 設計用モデル(コントローラ設計時のモデルのパラメータ)
A_nom = [1, 1; 0, 1];
B_nom = [0.5; 1];
C = [1, 0];
// 設計したゲイン(アッカーマンの公式より算出)
F = [1, 1.5];
G = [2; 1];
// 実際のシステム(現実の物理特性に5%の誤差を導入)
// 例:摩擦や慣性が変わり、Aの成分が少しズレる場合を考える
A_real = [1.05, 1; 0, 1.05];
B_real = [0.55; 1.05]; // 入力ゲインも10%ズレたと仮定
// シミュレーション設定
N = 30;
x = zeros(2, N+1);
x_hat = zeros(2, N+1);
u = zeros(1, N);
x(:,1) = [2; -1];
x_hat(:,1) = [0; 0];
// シミュレーションループ
for k = 1:N
y = C * x(:,k);
u(k) = -F * x_hat(:,k);
// 真のシステムは A_real, B_real で動く
x(:,k+1) = A_real * x(:,k) + B_real * u(k);
// 観測器は設計モデル A_nom, B_nom で計算する
x_hat(:,k+1) = A_nom * x_hat(:,k) + B_nom * u(k) + G * (y - C * x_hat(:,k));
end
// 結果のプロット
t = 0:N;
subplot(2,1,1);
plot(t, x(1,:), 'b-o'); xgrid();
ylabel('Position (x1)');
title('Mismatched Model: Deadbeat Control (Oscillation occurs)');
subplot(2,1,2);
plot(t, x(2,:), 'r-x'); xgrid();
xlabel('Steps (k)');
ylabel('Velocity (x2)');
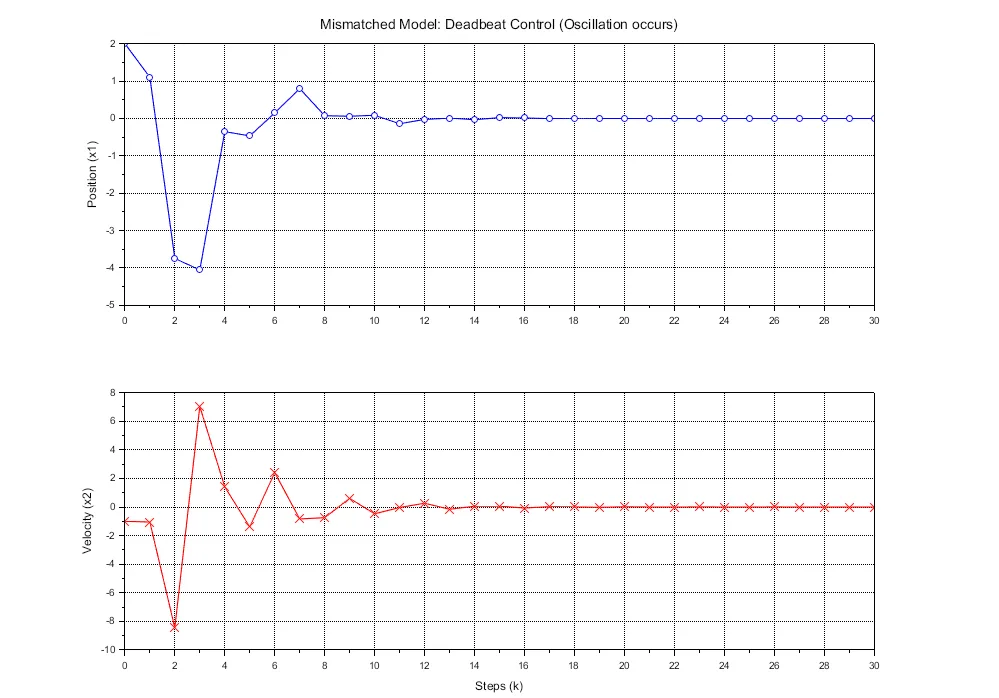
図2に示すように制御対象のモデルと実際のシステムに誤差があると、理想的なケースとは異なる挙動が見られる。デッドビート制御の極配置(\(z=0\))は、数学的には「z平面の原点でポール・ゼロ相殺(極零相殺)」を行っていることに相当する。理想状態のように設計モデルと現実が一致していれば、極が完全に原点に重なり、状態量は有限ステップで収束する。しかし、誤差がある状態では、現実の極が原点からズレる。これにより、ズレた極が\(Z\)平面の単位円の外側に出てしまうと、システムは不安定になる。