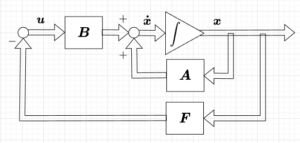
27. PIDと状態フィードバック
PID制御と「状態観測器(オブザーバ)を用いた状態フィードバック」は、一見すると異なる手法に見えるが、制御の本質(過去・現在・未来の情報をどう使うか)において共通点がある。特に、2次系(位置と速度を扱うシステムなど)において、これらは数学的に等価な関係になることがある。
PID制御と「状態フィードバック + 状態観測器」の比較
それぞれの制御器が「何を使って制御入力(操作量)を決めているか」を整理する。
1)PID制御(出力フィードバック)
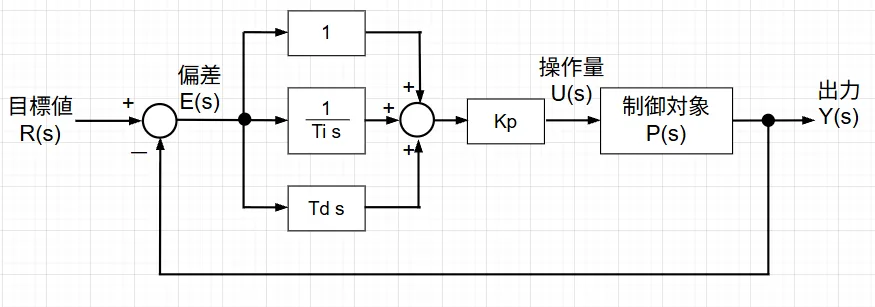
図1を参照しPID制御を見ると、観測できる出力\(Y(s)\;(y(t))\)と目標値 \(R(s)\;(r(t))\)の偏差\(E(s)\;(e(t))\) のみに注目していることが分かる。この偏差に対して以下の演算を行う。
・P(比例): 現在の偏差
・I(積分): 過去の偏差の蓄積
・D(微分): 未来の偏差の変化予測
※PID制御の詳細は、35. PID制御系を参照してください。
2)状態フィードバック + 状態観測器
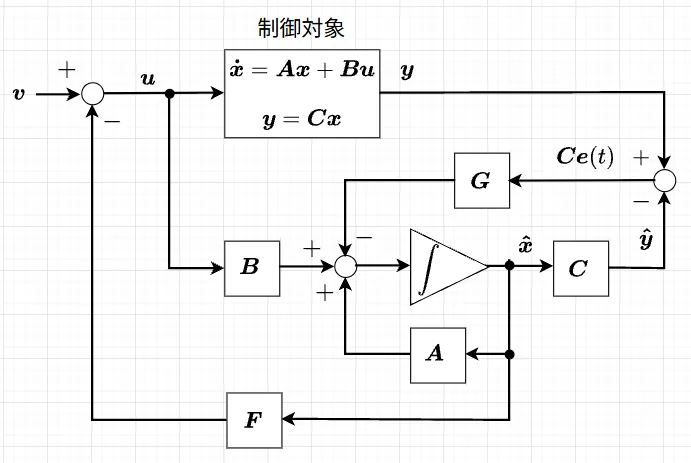
図2を参照し「状態フィードバック + 状態観測器」のシステムを見ると、システム内部のすべての変数(状態量\(x(t)\))を検出(推定)し、これを基にフィードバック制御を行う。
・状態フィードバック: \(u = -Fx\)。すべての状態量に重みをかけて制御入力を決定する。
・状態観測器(オブザーバ): 直接測れない状態量を、モデルを使って推定値 \(\hat{x}\)として算出する。
※状態フィードバック + 状態観測器の詳細は、17. オブザーバ併合型状態フィードバックを参照してください。
PIDと状態フィードバックの「等価性」
式(1)で示す\(n\)次の一入力一出力(SISO)線形システムを考える。$$\dot{\mathbf{x}}(t) = A\mathbf{x}(t) + \mathbf{b}u(t)\\ y(t) = \mathbf{c}\mathbf{x}(t) \; \quad \cdots \cdots (1)$$ここで、\(\mathbf{x}\)は\(n\)次の状態ベクトル、\(u\)は入力、\(y\)は出力である。
状態フィードバックによる「拡大系」
PID制御の「I(積分項)」を実現するために、誤差\(e(t) = r(t) - y(t)\)の積分値を新しい状態変数\(x_{n+1}\) として導入する(\(r\) は目標値)。$$\dot{x}_{n+1}(t) = e(t) = r(t) - \mathbf{c}\mathbf{x}(t) \; \quad \cdots (2)$$これにより、もとの\(n\)次のシステムに積分項を加えた\((n+1)\)次の拡大系が構成される。$$\begin{bmatrix} \dot{\mathbf{x}} \\ \dot{x}_{n+1} \end{bmatrix} = \begin{bmatrix} A & \mathbf{0} \\ -\mathbf{c} & 0 \end{bmatrix} \begin{bmatrix} \mathbf{x} \\ x_{n+1} \end{bmatrix} + \begin{bmatrix} \mathbf{b} \\ 0 \end{bmatrix} u + \begin{bmatrix} \mathbf{0} \\ 1 \end{bmatrix} r \; \quad \cdots (3) $$この拡大系に対する状態フィードバック則は次のように書ける。$$u = -\mathbf{F} \mathbf{x} + k_I x_{n+1} \; \quad \cdots (4)$$(ここで \(\mathbf{F}\)は状態に対するゲイン、\(k_I\)は積分項に対するゲイン。)
多くの物理システムで一般的な2次系(\(n=2\))を例に、PIDゲインとの直接的な対応を示す。状態を \(x_1 = y\)(位置)、\(x_2 = \dot{y}\)(速度)とすると、式(4)より、フィードバック則は、$$u = -f_1 x_1 - f_2 x_2 + k_I \int e dt \; \quad \cdots (5)$$となる。
一方、PID制御則では、$$u = K_p(r - y) + K_i \int (r - y) dt + K_d \frac{d}{dt}(r - y) \; \quad \cdots (6)$$目標値\(r\)が一定(\(\dot{r}=0\))と仮定して整理すると、$$u = K_p r - K_p y + K_i \int e dt - K_d \dot{y} \; \quad \cdots (6)$$となる。
式(5)と式(6)を比較すると、以下の対応関係が導かれる。
・比例ゲイン: \(K_p = f_1\) (ただし、目標値\(r\)への応答については、拡大系の構造により\(K_p\) 相当の重みが自動的に決まる)
・微分ゲイン:\(K_d = f_2\)
・積分ゲイン:\(K_i = k_I\)
以上より、次のことが言える。
1)PID制御器の3つのパラメータ(\(K_p, K_i, K_d\))を調整することは、拡大系(3次系)の3つの固有値(極)を自由に配置することと数学的に等価である。
2)システムが3次以上(\(n \ge 3\))の場合、標準的なPID(パラメータ3つ)ではすべての状態を独立に制御しきれない(すべての極を自由に配置できない)。この場合、状態観測器を用いてすべての状態を推定し、全状態フィードバックを行う必要がある。
3)PIDにおける「D項(微分)」は、状態変数のうち「速度」を直接測っている(あるいは近似的に求めている)ことに相当する。状態観測器を使う手法は、この「微分」をよりノイズに強く、かつ正確に行うための一般化された枠組みといえる。
また、このことからリカッチ方程式(LQR)を解いて得られた最適ゲイン\(K\)を、PIDの各値に逆算して設定することが可能と考えられる。
状態フィードバックゲインからPIDパラメータへの変換
DCモータの角度制御を例に、「状態フィードバックゲインを計算し、それをPIDパラメータに変換する」具体的な流れを考える。
制御対象(DCモータ)のモデル化
DCモータの回転角\(\theta\)を制御する場合、角速度を\(\omega = \dot{\theta}\)とすると、簡易的な物理モデルは以下の2次系で表される。
・状態量:\(x_1 = \theta\)(角度), \(x_2 = \dot{\theta}\)(角速度)
・状態方程式:$$\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 0 & -a \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} 0 \\ b \end{bmatrix} u$$(\(a\)は摩擦と慣性による時定数、\(b\)はトルク定数に関連するゲイン)
積分項を含めた拡大系
定常偏差をゼロにするために、偏差\(e = r - y = r - x_1\)の積分項\(x_3\)を追加する。$$\dot{x}_3 = r - x_1$$これを加えた3次系の拡大状態方程式は以下のようになる。$$\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \end{bmatrix} = \underbrace{\begin{bmatrix} 0 & 1 & 0 \\ 0 & -a & 0 \\ -1 & 0 & 0 \end{bmatrix}}_{A_e} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} + \underbrace{\begin{bmatrix} 0 \\ b \\ 0 \end{bmatrix}}_{B_e} u + \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} r$$
状態フィードバックゲインの設計
極配置法などを用いて、望ましい応答特性(速応性や安定性)を持つフィードバックゲイン\(\mathbf{F} = [f_1, f_2, -f_3]\)を設計したとする。制御入力 \(u\)は以下のようになる。$$u = -f_1 x_1 - f_2 x_2 + f_3 x_3$$※極配置法に関しては、14. 状態フィードバック を参照してください。
PIDパラメータへの変換
ここで標準的なPID制御則と比較する。$$u = K_p (r - y) + K_i \int (r - y) dt + K_d \frac{d}{dt}(r - y)$$目標値\(r\)を一定(\(\dot{r}=0\))とすると、
・\(y = x_1\)
・\(\frac{d}{dt}(r - y) = -\dot{x}_1 = -x_2\)
・\(\int (r - y) dt = x_3\)
これらを代入して整理すると、$$u = K_p r \underbrace{- K_p x_1}_{P} \underbrace{- K_d x_2}_{D} \underbrace{+ K_i x_3}_{I}$$状態フィードバックの式\(u = -f_1 x_1 - f_2 x_2 + f_3 x_3\)と係数を比較すると、以下の関係が導かれる。$$\begin{cases} K_p = f_1 / b \\ K_i = f_3 / b \\ K_d = f_2 / b \end{cases}$$※ \(b\)はシステムの入力ゲインである。
上記の方法によるPIDパラメータ調整には、以下の利点がある。
・極配置法を使うことで、オーバーシュートをどれくらいに抑え、何秒で収束させるかという仕様から、PIDパラメータ変換により\(K_p,\; K_i,\; K_d\)を一意に決定できる。
・リカッチ代数方程式を解いて(LQR法)フィードバックゲインを設計し、PIDパラメータ変換すれば、消費エネルギーを最小にしつつ、最速で目標値に到達する最適なPIDのパラメータ設定が得られる。
・モータの軸がたわむような複雑な系(4次系など)の場合、PID制御では限界があるが、この手法を使えば「どの状態がPIDのどの項に対応しているか」を把握しつつ、不足している情報を補うための状態観測器と状態フィードバックによる設計へスムーズに移行できる。