8. 切換超平面の設計（2）

最適切換超平面の設計法

式(1)のシステムに対して、スライディングモード制御になってからの状態の変動を最小にする最適な切換超平面を求めることを考える。$$\begin{cases} \dot x_1 = A_{11} x_1 + A_{12} x_2 \\ \dot x_2 = A_{21} x_1 + A_{22} x_2 + B_2 u \\ \sigma = S_1 x_1 + S_2 x_2 \end{cases} \;\;\; \cdots (1)$$ここで、式(2)の評価関数を導入する。$$J = \int_{t_s}^t x^T Q x dt \;\;\; \cdots (2)$$　\(Q\)は、$$Q = \begin{bmatrix} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{bmatrix}, \quad Q_{21}^T = Q_{12}, \quad Q \gt 0$$とする。また、\(t_s\)は状態\(x\)がスライディングモードに入ったときの時刻である。このとき、$$J = \int_{t_s}^t (x_1^T Q_{11} x_1 + 2 x_1^T Q_{12} x_2 + x_2^T Q_{22} x_2)dt$$に展開できる。 補助変数\(v\)を式(3)に設定する。$$v = x_2 + Q_{22}^{-1}Q_{12}^T x_1 \;\;\; \cdots (3)$$これにより、式(2)の評価関数は、$$J = \int_{t_s}^t (x_1^T Q_{11}^* x_1 + v^T Q_{22} v )dt \;\;\; \cdots (4)$$となる。ここで、\(Q_{11}^* = Q_{11} - Q_{12}Q_{22}^{-1} Q_{12}^T\)である。また、システムの状態方程式も補助変数\(v\)を用いて書き換えると、$$\dot x_1 = A_{11} x_1 + A_{12} x_2 = \left(A_{11} - A_{12} Q_{22}^{-1} Q_{12}^T\right) x_1 + A_{12} v$$すなわち、$$\dot x_1 = A_{11}^* x_1 + A_{12} v \quad \cdots (5)$$ここで、\(A_{11}^* = A_{11} - A_{12} Q_{22}^{-1} Q_{12}^T\)​である。式(4)、式(5)は最適制御問題となっており、これを解いて最適な切換超平面の傾き\(S\)を求める。式 (4) の評価関数\(J\)を最小化する最適制御入力\(v\)を求める問題は、線形二次レギュレータ（LQR）問題に帰着する。この最適制御問題に対する解の形式は、\(v = -R^{-1} B^T P x_1\)今回の問題において、入力行列\(B = A_{12}\)​、重み行列 \(R = Q_{22}\)​、状態重み行列は \(Q_{11}^*\) と解釈できるため、最適入力は、 $$v = -Q_{22}^{-1} A_{12}^T P x_1 \;\;\; \cdots (6)$$​である。また、このとき、行列 \(P\)は次のリカッチ方程式を満たす必要がある。$$PA_{11}^* + A_{11}^T P - PA_{12}Q_{22}^{-1}A_{12}^TP + Q_{11}^*= 0 $$式(3)より、$$x_2 = v - Q_{22}^{-1}Q_{12}^T x_1 = -Q_{22}^{-1}(A_{12}^T P + Q_{12}^T)x_1$$なので、$$(A_{12}^TP + Q_{12}^T)x_1 + Q_{22} x_2= 0$$となり、$$\sigma = [S_1 \quad S_2]x$$である。ここで、$$ S = [A_{12}^TP + Q_{12}^T \quad Q_{22}] \;\;\; \cdots (7)$$として、スライディングモードを生じさせると、\(J\)を最小にする制御系を構成できる。
※最適制御問題については、19. 最適フィードバック制御、25. 最適レギュレータ、17. 離散時間系の最適レギュレータを参照してください。

最適切換超平面の例（倒立振子）

倒立振子の非線形運動方程式（ダンパーあり）は、\(I\)：慣性モーメント、\(D\)：回転に対する粘性減衰係数（ダンパー）、\(m\)：振子の質量、\(L\)：回転軸から重心までの距離、\(\tau\)：振子に加えるトルク（制御入力）として、$$I \ddot{\theta} - mgL \sin \theta + D \dot{\theta} = \tau$$である。倒立点 \(\theta \approx 0\)の周りで線形化すると \(\sin \theta \approx \theta\)なので、$$I \ddot{\theta} - mgL \theta + D \dot{\theta} \approx \tau$$ $$\ddot{\theta} \approx \frac{mgL}{I} \theta - \frac{D}{I} \dot{\theta} + \frac{1}{I} \tau$$状態変数を $$x = \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix}$$ と定義すると、線形化された状態空間表現は $$\dot{x} = Ax + Bu$$ と書ける。$$\begin{bmatrix} \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ mgL/I & -D/I \end{bmatrix} \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 1/I \end{bmatrix} \tau $$ ここで、$$A = \begin{bmatrix} 0 & 1 \\ \frac{mgL}{I} & -\frac{D}{I} \end{bmatrix}, \quad B = \begin{bmatrix} 0 \\ \frac{1}{I} \end{bmatrix}, \quad u = \tau$$
システム表現は以下となる。$$\begin{cases} \dot{x}_1 = A_{11}x_1 + A_{12}x_2 \\ \dot{x}_2 = A_{21}x_1 + A_{22}x_2 + B_2 u \end{cases} $$ 全状態ベクトル $$x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$$ 倒立振子の場合、全状態ベクトルは $$ \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix} $$で2次元である。ここでは \(x_1 = \theta \)（1次元）, \(x_2 = \dot{\theta} \)（1次元）と分割する。この分割に対応して、A, B をブロック分割すると、$$A = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ \frac{mgL}{I} & -\frac{D}{I} \end{bmatrix}, \quad B = \begin{bmatrix} B_1 \\ B_2 \end{bmatrix} = \begin{bmatrix} 0 \\ \frac{1}{I} \end{bmatrix}$$ 切換超平面は、$$\sigma = S_1 x_1 + S_2 x_2 = S_1 \theta + S_2 \dot{\theta}$$ 評価関数を$$J = \int_{t_s}^t \left( x_1^T Q_{11}^* x_1 + v^T Q_{22} v \right) dt$$として、以下のリカッチ方程式を解く。$$P A_{11}^* + A_{11}^{T} P - P A_{12} Q_{22}^{-1} A_{12}^T P + Q_{11}^* = 0$$ここで、$$A_{11}^* = A_{11} - A_{12} Q_{22}^{-1} Q_{12}^T$$ $$Q_{11}^* = Q_{11} - Q_{12} Q_{22}^{-1} Q_{12}^T$$スカラーにすると、リカッチ方程式は、$$2 P A_{11}^* - P^2 A_{12}^2 Q_{22}^{-1} + Q_{11}^* = 0$$となる。各パラメータを代入すると、$$2 P A_{11} Q_{22} - 2 P Q_{12} - P^2 + Q_{11} Q_{22} - Q_{12}^2 = 0$$ $$P^2 + (2 Q_{12} - 2 A_{11} Q_{22}) P - (Q_{11} Q_{22} - Q_{12}^2) = 0$$これは \(P\) に関する2次方程式であり、正の解を採用する。得られた \(P\)を使って切換超平面の係数は、$$S_1 = A_{12}^T P + Q_{12}^T, \quad S_2 = Q_{22}$$となる。スカラーの場合、$$S_1 = A_{12} P + Q_{12}, \quad S_2 = Q_{22}$$なので、非線形ダイナミクス用の制御入力は、$$\dot{\sigma} = S_1 \dot{\theta} + S_2 \ddot{\theta}= S_1 \dot{\theta} + S_2 \cdot \frac{1}{I} \left( mgL \sin \theta - D \dot{\theta} + \tau \right)$$より、等価制御は、$$S_1 \dot{\theta} + \frac{S_2}{I} \left( mgL \sin \theta - D \dot{\theta} + \tau_{eq} \right) = 0$$ $$\tau_{eq} = - \left( \frac{I S_1}{S_2} + D \right) \dot{\theta} - mgL \sin \theta $$である。切換制御（チャタリング対策）を、$$\tau_{sw} = -K \cdot \tanh\left( \frac{\sigma}{\Phi} \right)$$として、全体の制御入力は、$$\tau = \tau_{eq} + \tau_{sw}$$となる。

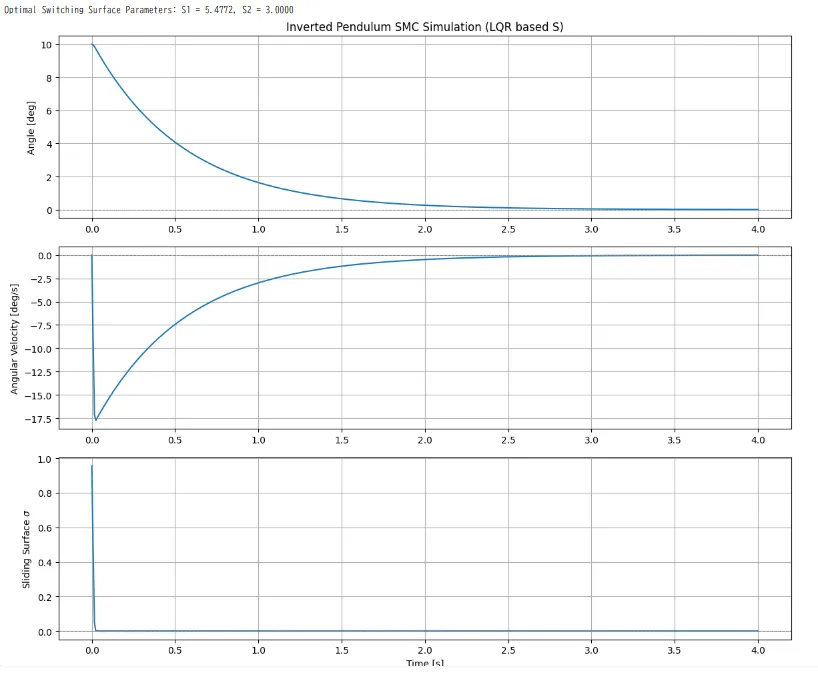
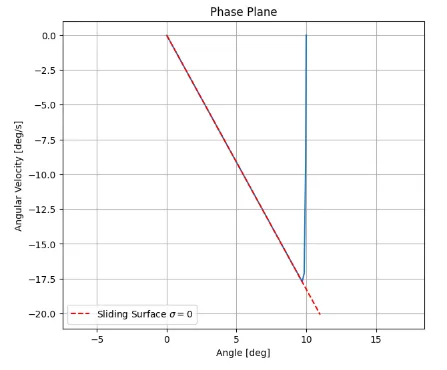
Pythonスクリプトとシミュレーション結果を示す。図１は、振子の角度、角速度、及び切換超平面\(\sigma\)の時間応答である。角速度が-17.5近傍で切換超平面に到達し、スライディングモードに入っている。スライディングモードでは、振子角度が滑らかに変化して０度（倒立状態）に達している。当然、振子角速度は０となっている。図２は、角度と角速度の位相平面図で、初期角度（10度）から素早く切換超平面に到達して、原点（倒立状態）にスライディングモードで達していることが分かる。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from scipy.linalg import solve_continuous_are, inv
# --- システムパラメータ ---
m = 1.0  # 質量 [kg]
L = 1.0  # 重心までの長さ [m]
g = 9.81 # 重力加速度 [m/s^2]
I = m * L**2 # 慣性モーメント (質点と仮定) [kg m^2]
D = 0.1 # 粘性減衰係数 [Nm s/rad]
# --- LQRによる最適切換超平面の設計 ---
# 線形化システム行列 (A, B)
# state: [theta, theta_dot]
A_linear = np.array([
    [0, 1],
    [m * g * L / I, -D / I]
])
B_linear = np.array([
    [0],
    [1 / I]
])
# フレームワークの分割に対応させる (x1=[theta], x2=[theta_dot], u=[tau])
A11 = np.array([[A_linear[0, 0]]]) # スカラーを1x1行列として扱う
A12 = np.array([[A_linear[0, 1]]])
A21 = np.array([[A_linear[1, 0]]])
A22 = np.array([[A_linear[1, 1]]])
B2  = np.array([[B_linear[1, 0]]])
# 評価関数 J = int(x^T Q x) dt の重み行列 Q
# Q は 2x2 行列 [ Q11 Q12 ]
#              [ Q21 Q22 ]
# Q > 0 かつ Q21^T = Q12 を満たすように選択
# Q11, Q12, Q22 はフレームワークの分割に対応した行列 (ここでは全て1x1)
# 例として、Q12=0 とし、Q11, Q22を対角成分として設定
Q11_lqr = np.array([[10.0]]) # 角度偏差を重視
Q12_lqr = np.array([[0.0]])
Q22_lqr = np.array([[3.0]])  # 角速度偏差を重視
# フレームワーク内のQ*11とA*11を計算
# Q*11 = Q11 - Q12 @ inv(Q22) @ Q12.T
Q11_star = Q11_lqr - Q12_lqr @ inv(Q22_lqr) @ Q12_lqr.T
# A*11 = A11 - A12 @ inv(Q22) @ Q12.T
A11_star = A11 - A12 @ inv(Q22_lqr) @ Q12_lqr.T
# リカッチ方程式を解いて行列 P を求める
# 方程式形式: (A*11)^T P + P A*11 - P A12 Q22^-1 A12^T P + Q*11 = 0
# scipy.linalg.solve_continuous_are(A, B, Q, R) は A^T P + P A - P B R^-1 B^T P +
Q = 0 を解く
# ここでは A -> A11_star, B -> A12, Q -> Q11_star, R -> Q22_lqr
P = solve_continuous_are(A11_star.T, A12, Q11_star, Q22_lqr)
# 求めた P から最適な切換超平面の係数 S1, S2 を計算
# S = [ S1 S2 ] = [ A12^T P + Q12^T   Q22 ]
S1 = A12.T @ P + Q12_lqr.T
S2 = Q22_lqr
# スカラー値として取り出す
S1_smc = S1[0, 0]
S2_smc = S2[0, 0]
print(f"Optimal Switching Surface Parameters: S1 = {S1_smc:.4f}, S2 = {S2_smc:.4f}")
# --- SMC制御ゲイン (設計パラメータ) ---
K_smc = 20.0    # 切換ゲイン (調整可能)
phi_smc = 0.1   # 境界層の厚さ (調整可能)
# --- システムのODE関数 (非線形ダイナミクスを使用) ---
def pendulum_ode(t, x, params, s_params, control_gains):
    theta, theta_dot = x
    m, L, g, I, D = params
    S1, S2 = s_params
    K, phi = control_gains
    # 切換超平面 s の計算
    sigma = S1 * theta + S2 * theta_dot
    # 制御入力 tau の計算 (非線形ダイナミクスに基づく等価制御 + tanh近似による切換制御)
    # tau_eq = (D - I * S1/S2) * theta_dot - m * g * L * np.sin(theta) # スカラーの場合の等価制御
    tau_eq = (D - I * (S1/S2)) * theta_dot - m * g * L * np.sin(theta) # スカラー演算
    tau_sw = -K * np.tanh(sigma / phi) # tanh近似
    tau = tau_eq + tau_sw
    # 運動方程式
    theta_ddot = (m * g * L * np.sin(theta) - D * theta_dot + tau) / I
    return [theta_dot, theta_ddot]
# --- シミュレーション実行 ---
# 初期条件 [角度(rad), 角速度(rad/s)]
# 鉛直上向き (0) から少しずれた状態から開始
initial_state = [np.deg2rad(10), 0.0] # 例: 10度から静止状態で開始
# シミュレーション時間
t_span = [0, 4.0] # 0秒から4秒までシミュレーション
t_eval = np.linspace(t_span[0], t_span[1], 500) # 評価する時間点
# パラメータをまとめる
system_params = (m, L, g, I, D)
smc_surface_params = (S1_smc, S2_smc)
smc_control_gains = (K_smc, phi_smc)
# ODEソルバーを実行
result = solve_ivp(
    pendulum_ode,
    t_span,
    initial_state,
    t_eval=t_eval,
    args=(system_params, smc_surface_params, smc_control_gains),
    dense_output=True # 密な出力を有効にする (必要に応じて)
)
# 結果の取得
t = result.t
states = result.y # states[0]はtheta, states[1]はtheta_dot
theta = states[0, :]
theta_dot = states[1, :]
# 切換超平面 s の軌跡を計算 (設計した S1, S2 を使用)
sigma_trajectory = S1_smc * theta + S2_smc * theta_dot
# --- プロット ---
plt.figure(figsize=(12, 10))
# 角度 vs 時間
plt.subplot(3, 1, 1)
plt.plot(t, np.rad2deg(theta))
plt.axhline(0, color='gray', linestyle='--', linewidth=0.8)
plt.ylabel('Angle [deg]')
plt.title('Inverted Pendulum SMC Simulation (LQR based S)')
plt.grid(True)
# 角速度 vs 時間
plt.subplot(3, 1, 2)
plt.plot(t, np.rad2deg(theta_dot))
plt.axhline(0, color='gray', linestyle='--', linewidth=0.8)
plt.ylabel('Angular Velocity [deg/s]')
plt.grid(True)
# 切換超平面 σ vs 時間
plt.subplot(3, 1, 3)
plt.plot(t, sigma_trajectory)
plt.axhline(0, color='gray', linestyle='--', linewidth=0.8)
plt.ylabel('Sliding Surface $\sigma$')
plt.xlabel('Time [s]')
plt.grid(True)
plt.tight_layout()
plt.show()
# 位相空間プロット
plt.figure(figsize=(7, 6))
plt.plot(np.rad2deg(theta), np.rad2deg(theta_dot))
# 切換超平面 σ=0 (S1*theta + S2*theta_dot = 0 より theta_dot = -(S1/S2)*theta)
theta_vals_deg = np.linspace(np.rad2deg(np.min(theta)) * 1.1,
np.rad2deg(np.max(theta)) * 1.1, 100)
s_zero_line_deg = -(S1_smc / S2_smc) * theta_vals_deg
plt.plot(theta_vals_deg, s_zero_line_deg, 'r--', label='Sliding Surface $\sigma=0$')
plt.xlabel('Angle [deg]')
plt.ylabel('Angular Velocity [deg/s]')
plt.title('Phase Plane')
plt.grid(True)
plt.legend()
plt.axis('equal') # 軸のスケールを合わせる
plt.show()