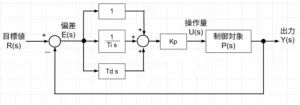
30. インピーダンス制御
インピーダンス制御(Impedance Control)は、ロボットの先端(エンドエフェクタ)と環境との間の「動的な関係(力と運動の関係)」を操るための制御手法である。これまでの「位置制御」や「力制御」とは異なり、ロボッ […]
28. 外乱オブザーバ
外乱オブザーバ(Disturbance Observer: DOB)は、モータ制御などの精密なモーションコントロールにおいて、負荷トルクの変動や摩擦、モデルの不確かさを「外乱」として一括して推定し、その「外乱」打ち消すた […]
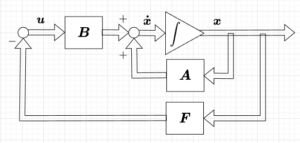
13-1. オブザーバ併合型状態フィードバックによるデッドビート制御
デッドビート制御(有限時間整定制御)は、離散時間システム特有の制御手法で、「サンプリング周期の整数倍という有限の時間内に、状態誤差を完全にゼロにする」という強力な応答特性を持つ制御である。ここでは、これを状態観測器(オブ […]
27. PIDと状態フィードバック
PID制御と「状態観測器(オブザーバ)を用いた状態フィードバック」は、一見すると異なる手法に見えるが、制御の本質(過去・現在・未来の情報をどう使うか)において共通点がある。特に、2次系(位置と速度を扱うシステムなど)にお […]
19-1. リッカチ代数方程式
最適制御、特に線形二次レギュレータ(LQR)の問題において、無限時間評価関数を最小化する際に現れるのがリッカチ代数方程式(Algebraic Riccati Equation, ARE)である。ここでは、リッカチ代数方程 […]
6-2. ラプラス変換(アプリの利用)
ラプラス変換は工学、特に電気電子工学、制御工学、信号処理の分野において、強力な数学的ツールである。その最大の効用は、「微分方程式の解法を、代数方程式の解法に置き換える」ことによって、複雑な時間応答解析を容易にすることであ […]
12-1. 可制御正準形への変換(演習)
※可制御正準形への変換に関しては、12. 可制御正準形を参照。 対象とする状態方程式と出力方程式は$$\dot{x}(t) = Ax(t) + bu(t) \\ y(t) = Cx(t) \quad \cdots (1) […]
40. 実積分への応用(複素関数)
積分計算の手順 \(I=\int_C f(z) dz \)を計算する。1)\(f(z)\)の極で\(C\)の内部にあるもの\(\alpha_1,\alpha_2,\cdots,\alpha_n\)を求める。2)留数\(\ […]
39. 留数定理(複素関数)
ローラン展開において、\(f(z)_1\)と\(f(z)_2\)の級数はそれぞれ収束し、その和が左辺\(f(z)\)に一致する。また、\(f(z)\)が穴あき円板\(D = \{z \in \mathbb{C}\;|\; […]
38. べき級数展開(複素関数)
べき級数展開は、複素関数論における正則関数の解析的な性質と密接に結びついており、実関数の定積分を計算する際に強力なツールとなる。例えば、高階導関数の公式$$f^{(n)}(\alpha) = \frac{n!}{2 \p […]
37. コーシーの積分公式(複素関数)
コーシーの積分定理と同じ仮定の下で、コーシーの積分公式が成立する。 【証明(概要)】証明したい積分を\(I\)とする。 $$I = \int_C \frac{f(z)}{z - \alpha} dz$$点\(\alpha […]
36. 積分定理の応用と証明(複素関数)
【証明(概要)】・\(\alpha\)が\(C\)の外部にあるとき:関数\(f(z) = \frac{1}{z - \alpha}\)は、曲線\(C\)およびその内部を含む領域\(D\)で正則である。特異点\(\alph […]
35. コーシーの積分定理(複素関数)
まず、複素線積分を計算可能な積分に置き換えることを考える。 複素関数\(f(z)\)および曲線\(C\)上の微小変位\(dz\)を、実部と虚部に分解する。 ここで、\(z = x + j y\)とする。\(f(z) = […]
34. 複素線積分(複素関数)
複素線積分においてコーシー・リーマンの定理が重要である。コーシー・リーマンの定理は、関数が正則(複素微分可能)であるための必要十分条件を与え、複素関数論の主要な成果は、この「正則性」という性質に大きく依存する。 リーマン […]
33. コーシー・リーマンの定理(複素関数)
まず、導関数(複素関数)の公式をまとめておく。 公式 4)合成関数の微分法則の証明(概略):\(h(z) = g(f(z))\)とおく。\(h(z)\)の微分\(h'(z)\)は、微分の定義により次の極限として与えられる […]
32. 複素関数の微分(複素関数)
実関数における「微分」の役割は、関数のグラフを接線(1 次関数)で近似することで各点における関数の局所的な変化を表現するものである。複素関数の場合も同様で、関数はある点をある点に写すことになるのだが、その局所的な作用を1 […]
31. 関数の極限と連続性(複素関数)
複素関数の極限は、実数関数の極限と基本的な考え方は同じであるが、複素数特有の性質があるため、より厳密な理解が必要である。 ※ (1)の\(|z - \alpha| \rightarrow 0\)は実数の意味なので、実数と […]
30. 三角関数(複素関数)
\(\theta \in \mathbb{R}\)のとき、指数関数の定義から\(e^{j \theta} = \cos \theta + j \sin \theta\)(オイラーの公式)が成立する。この式の\(\thet […]
29. 複素数べき(複素関数)
複素数べき(複素数の複素数乗):複素数\(z \neq 0\)と複素数\(w\)にたいし、「\(z\)の\(w\)乗」を$$z^w := e^{w \log z}$$と定義する。ただし、\(\log z\)は複素数の対数 […]