5. カルノー図による論理式の簡単化
カルノー図は、論理回路や論理関数を視覚的に表現するための図形ツールである。主に2進数変数を持つ論理関数を簡単化するために用いられる。カルノー図は、真理値表から得られる情報を整理し、最適な論理回路の設計や単純化に役立つ。
カルノー図の基本的な特徴と使用法を以下に示す。
サイズと配置:カルノー図は、入力変数が\(n\)個の場合、\(2^n\)個のセルを持つ正方形の格子状の図となる。各セルは、入力変数の可能な組み合わせ(最小項)に対応している。
セルの値:各セルには、論理関数の出力に対応する真理値を表示する。
グルーピング:隣り合ったセルをまとめてグループに分け、特定の条件を満たす最小項の集合を表現する。グループは2の冪数 \(2^n \;\;\;(n=0,1,2,\cdots)\) として表現され、できるだけ大きなグループを作ることが目標となる。
論理関数の単純化:カルノー図上でグルーピングされた領域において、その領域内のセルに対応する最小項を論理和(OR)で結合することで、論理関数を単純化することが可能となる。
以上により、最小な論理ゲートの組み合わせで関数を実現することができる。
カルノー図は、論理関数の視覚的な理解と単純化に有効であるが、入力変数が多いと図示が難しくなるため、実用的に使うというより、論理関数の視覚的な理解に使用される。
カルノー図の作成
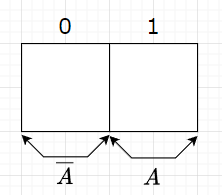
図1は、論理変数が\(A\)だけの場合のカルノー図である。
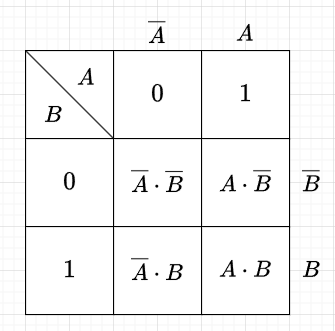
図2は、論理変数が\(A,\;B\)の2種類の場合のカルノー図で、各セルが主加法標準形の最小項となる。
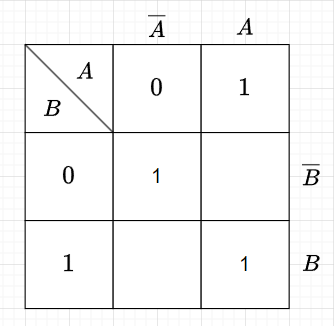
表1の真理値表をこの図2に適用すると図3のように表せる。
| \(A\) | \(B\) | \(Z\) | 最小項 |
| 0 | 0 | 1 | \(\overline{A} \cdot \overline{B}\) |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 | \(A \cdot B\) |
図3のカルノー図より、図2を参照して、出力\(Z\)が1となるセルの最小項の論理和をとることで、$$Z=f(A,B)=\overline{A} \cdot \overline{B} + A \cdot B$$として、論理関数\(f(A,B)\)が求まる。
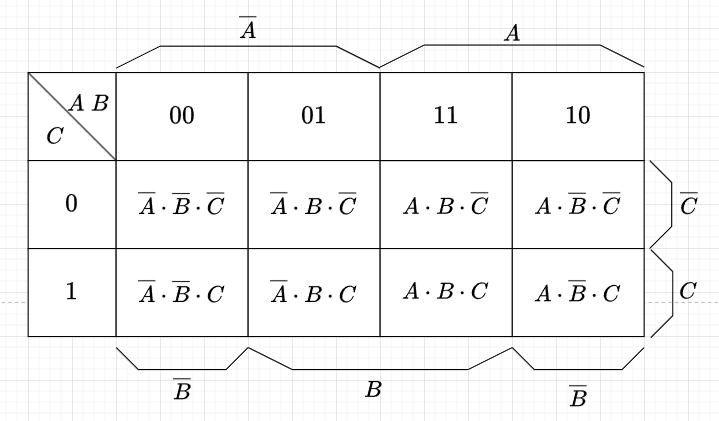
図4は、論理変数が\(A,\; B, \; C\)の3種類の場合のカルノー図で、各セルが主加法標準形の最小項となる。
論理式の簡単化
図5のカルノー図を考える。この図の最小項の論理和は、$$Z = A \cdot \overline{B} + A \cdot B$$となる。ここで、赤線で囲ったように隣のセルをまとめることができる。この赤線で囲まれたところは\(A\)だけで決まるので、$$Z=A \cdot \overline{B} + A \cdot B=A$$である。論理式の整理で示すと、$$Z=A \cdot \overline{B} + A \cdot B = A \cdot (\overline{B} + B) = A$$である。
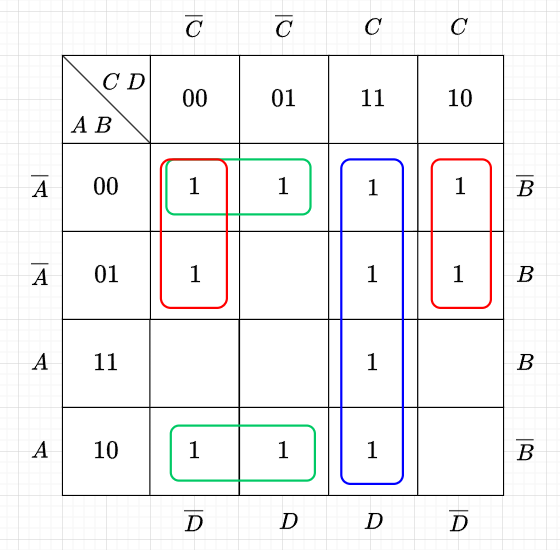
図6は、変数が\(A, \; B, \; C, \; D\)の 4種類の場合のカルノー図の例である。簡単化は以下の手順で行う。
・以下を原則として、図の中の全ての1を出来るだけ少ない長方形で囲むようにする。
1)長方形の中は全て1であること。
2)長方形の中の1の数は\(2^n\)であること。
3)同じセルを2つ以上の長方形で共有しても良い。
4)カルノー図の上下端、左右端は連続していると考える。
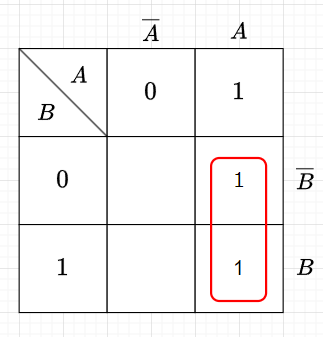
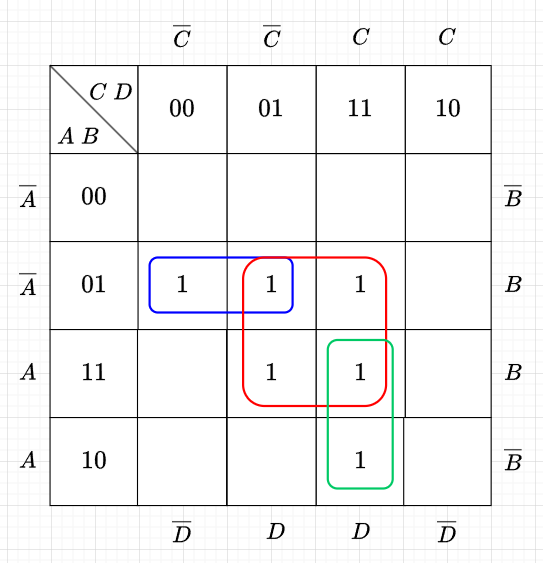
図6の最小項の論理和で論理関数を求めると、$$Z=f(A,B,C,D)\\ = \overline{A} \cdot B \cdot \overline{C} \cdot \overline{D} + \overline{A} \cdot B \cdot \overline{C} \cdot D + \overline{A} \cdot B \cdot C \cdot D + A \cdot B \cdot \overline{C} \cdot D + A \cdot B \cdot C \cdot D + A \cdot \overline{B} \cdot C \cdot D$$となる。
カルノー図から、論理関数を作るには、長方形の各ループから共通変数を取り出した論理積を作り、その論理和をとる。図6では、青ループは、\(\overline{A}\cdot B \cdot \overline{C}\)、緑ループは、\(A \cdot C \cdot D\)、赤ループは、\(B \cdot D\)となっている。従って、論理関数は、$$Z = f(A,B,C,D) = \overline{A}\cdot B \cdot \overline{C} + A \cdot C \cdot D + B \cdot D$$となる。これは、最小項の論理和で求めた論理関数が簡単化されている。
次の論理関数を簡単化する。$$Z = f(A,B,C,D) = A \cdot \overline{B} \cdot \overline{C} \cdot \overline{D} + \overline{A} \cdot \overline{B} \cdot \overline{C} + A \cdot \overline{B} \cdot D + \overline{A} \cdot C + \overline{A} \cdot B \cdot \overline{C} \cdot D + A \cdot B \cdot C \cdot D$$ この式からカルノー図を描くと図7のようになる。
図7より、青ループは、\(C \cdot D\)、緑ループは、\(\overline{B} \cdot \overline{C}\)、赤ループは、\(\overline{A} \cdot \overline{D}\)となっている。従って、理関数は、$$Z = f(A,B,C,D) = C \cdot D + \overline{B} \cdot \overline{C} + \overline{A} \cdot \overline{D}$$となる。なお、緑ループの上端と下端、赤ループの左端と右端はループが繋がっている。