38-1. I-P制御

制御対象をパワーエレクトロニクスであるモータ駆動回路（モータのコイル、すなわち、インダクタを駆動する電気回路）として、PI制御とI-P制御の相違を考える。
※I-P制御の具体例として、例えば、「ゲイン調整以外の制御性能の改善方法「I-P制御」とは」が参考になる。

PI制御とI-P制御の違いは、比例要素（P）と積分要素（I）の適用順序ではないことに注意する必要がある。
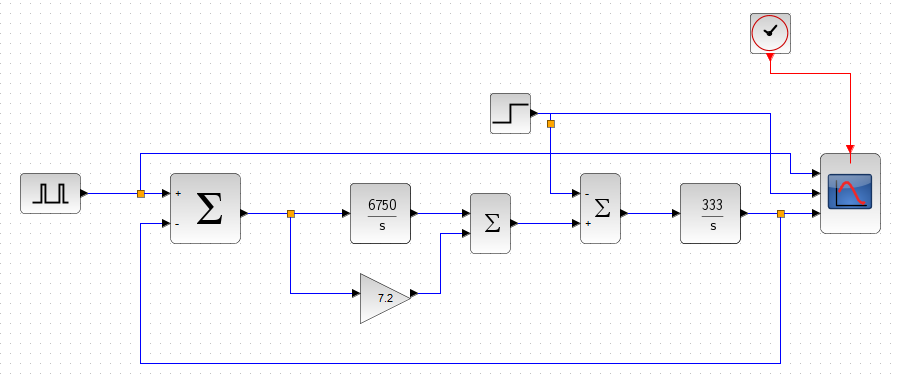
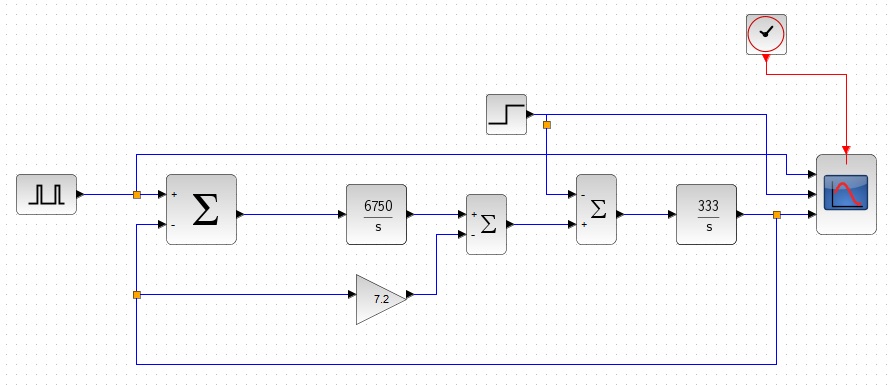
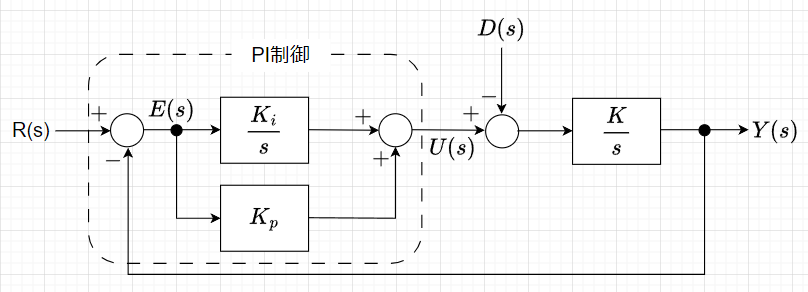
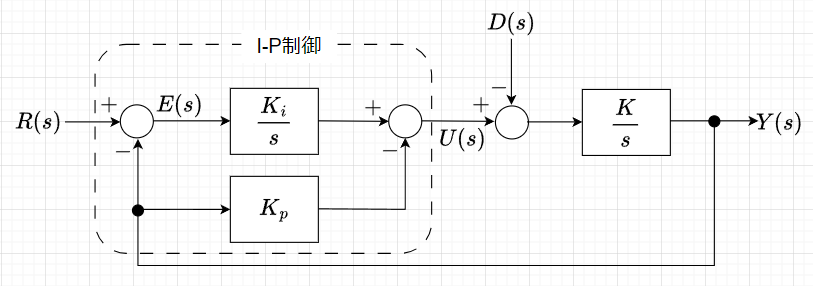
図１「PI制御の構成」と図２「I-P制御の構成」を見てわかるように、PI制御では偏差を基に比例要素、積分要素を作用させて操作量を得る。式で表すと$$U(s) =\left( \frac{K_i}{s} + K_p \right)E(s) \;\;\cdots (1)$$となる。一方、I-P制御では、偏差に積分要素を作用させた量から、出力に比例要素を作用させた量を減算したものから操作量を得る。式で表すと$$U(s) = \frac{K_i}{s} E(s) - K_p Y(s)\;\;\cdots(2) $$となる。

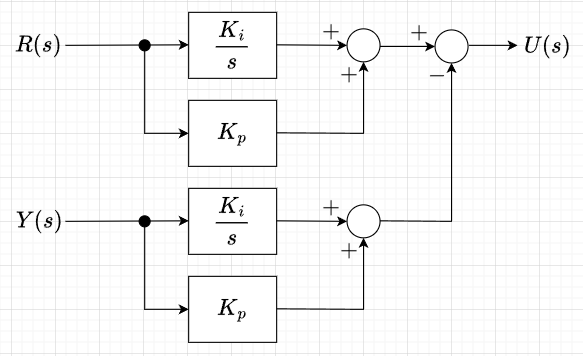
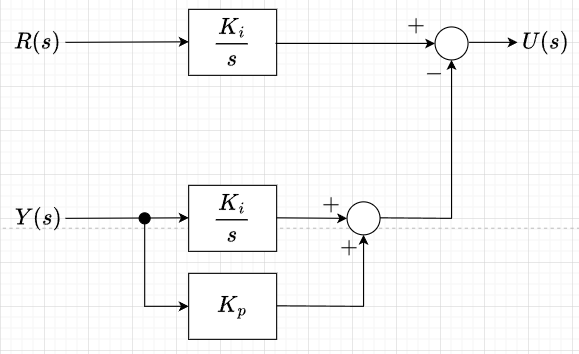
ここで、(1)式を変形すると、$$U(s)=(R(s)-Y(s))\left(\frac{K_i}{s} + K_p\right) \\=R(s)\left( \frac{K_i}{s} + K_p\right) - Y(s)\left( \frac{K_i}{s} + K_p\right) $$ となる。これをブロック図にすると図３「PI制御器の構造」のように表せる。一方、(2)式を変形すると、$$U(s) = (R(s) - Y(s))\frac{K_i}{s} - Y(s) K_p \\ = R(s) \frac{K_i}{s} - Y(s) \left(\frac{K_i}{s} + K_p\right)$$となる。これをブロック図にすると図４「I-P制御器の構造」のように表せる。
図３と図４を比べると、図３（PI制御）では、目標値\(R(s)\)に比例要素と積分要素が作用しており、図４（I-P制御）では、目標値\(R(s)\)に積分要素だけ作用している。つまり、I-P制御の場合、目標値\(R(s)\)の変化を緩やかにするように働くことになる。一方、出力\(Y(s)\)のフィードバックに関しては、PI制御でもI-P制御でも変わらない。すなわち、外乱\(D(s)\)や制御対象のバラツキなどによる変動の影響を抑制する働きは、PI制御もI-P制御も同等であると言える。

シミュレーションによる動作比較

Xcos（Scilabの時間領域シミュレーションツール）を使って、PI制御とI-P制御の時間応答特性を比較する。
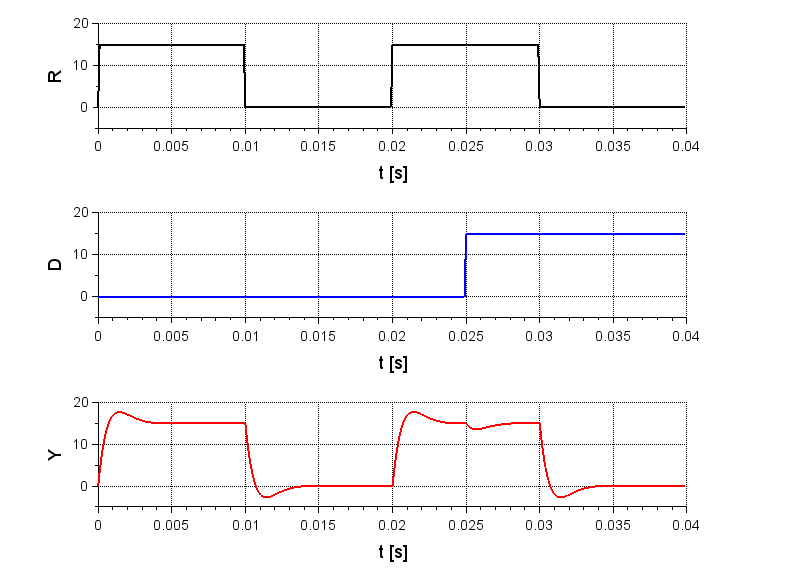
図５は「PI制御シミュレーション」である。制御対象は、パワーエレクトロニクスであるモータ駆動回路（モータのコイル、すなわち、インダクタを駆動する電気回路）を想定しており、制御対象の伝達関数は\(\frac{333}{s}\)で、積分特性である。図６が「PI制御シミュレーション結果」で、目標値\(R\)は周期的な矩形波で、外乱\(D\)はステップ状に変化するとする。出力\(Y\)は、目標値\(R\)に追従するように変化するが、若干のオーバーシュート（及びアンダーシュート）が見られる。また、ステップ状の外乱\(D\)が入ったとき（25 [ms]の部分)、出力\(Y\)が乱れるが、2 [ms]程度で抑圧できている。
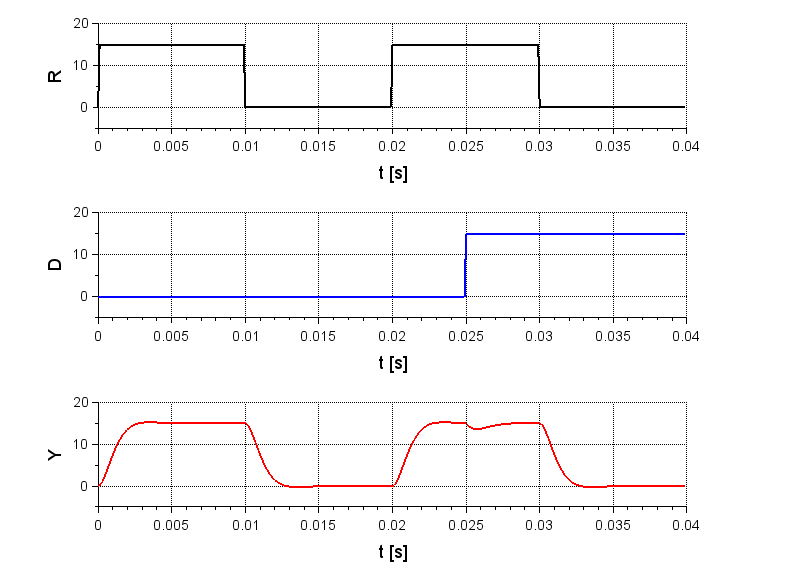
図７は同じ制御対象で、\(K_i , \;\;K_p\)とも同じ値にしたときの「I-P制御シミュレーション」である。出力\(Y\)は、PI制御の場合と比較して滑らかに目標値\(R\)に追従しており、オーバーシュート（及びアンダーシュート）がほとんど無い。ステップ状の外乱\(D\)が入ったときの応答はPI制御の場合と同様である。つまり、目標値に対する応答は改善し、外乱に対する応答は劣化しないことが分かる。

以上のように、I-P制御はPI制御と同じ制御要素（比例制御、積分制御）でフィードバックの構成の若干の変更で、目標値応答を改善し、外乱抑圧特性を変えないことができる。
ただし、実装においては各要素における飽和特性など（特に積分要素の飽和など）を十分に検討する必要がある。