23-1. ナイキストの安定判別法
図1「 フィードバック制御系」の特性方程式は、$$1+G(s)H(s)=0$$である。また、$$L(s)=G(s)H(s)$$を一巡伝達関数(開ループ伝達関数)という。いま、$$L(s)=G(s)H(s)=\frac{K(s-z_1)(s-z_2)\cdots(s-z_l)}{(s-p_1)(s-p_2)(s-p_3)\cdots(s-p_m)} \;\;\;\; (m \gt l)$$
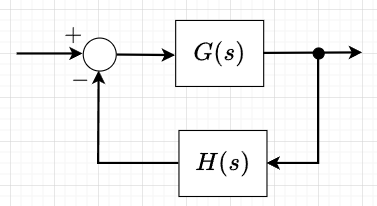
とすると、特性方程式は、$$1+\frac{K(s-z_1)(s-z_2)\cdots(s-z_l)}{(s-p_1)(s-p_2)(s-p_3)\cdots(s-p_m)}=0 \\ \frac{(s-p_1)(s-p_2)(s-p_3)\cdots(s-p_m) + K(s-z_1)(s-z_2)\cdots(s-z_l)}{(s-p_1)(s-p_2)(s-p_3)\cdots(s-p_m)}=0$$となる。この式の分子を因数分解すると、$$1+G(s)H(s)=\frac{(s-s_1)(s-s_2)(s-s_3)\cdots(s-s_m)}{(s-p_1)(s-p_2)(s-p_3)\cdots(s-p_m)}=0$$と表せる。従って、この零点\((s_1,s_2,s_3,\cdots,s_m)\)が特性根になる。この特性根の全てが複素平面の左半平面にあれば、フィードバック制御系は安定といえる。ナイキストの安定判別法は、この特性根を求めることなく安定性を判別し、さらに安定度を評価することができる手法である。
特性方程式のベクトル軌跡
図2「特性方程式のベクトル軌跡」のように特性根\(s_1\)のまわりを時計方向にかこむ\(s\)の経路\(L\)があるとして、経路上の点\(A\)へ各特性根\((s_1,s_2,\cdots)\)および、各極\((p_1,p_2,\cdots)\)からそれぞれベクトル\(s-s_1,s-s_2,\cdots\)および、\(s-p_1,s-p_2,\cdots\)を引くとする。特性方程式の左辺$$1+G(s)H(s)=\frac{(s-s_1)(s-s_2)(s-s_3)\cdots(s-s_m)}{(s-p_1)(s-p_2)(s-p_3)\cdots(s-p_m)} \cdots (1)$$は、これらのベクトルの乗除算によって構成されていることになる。
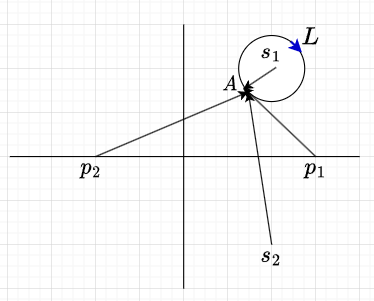
ここで、点\(A\)を経路\(L\)に沿って時計回りに1回転させると、\(L\)の中にある特性根\(s_1\)からのベクトル\(s-s_1\)の角度は負の方向(時計方向)に\(2\pi\)まで増加する。これに対して、他の特性根、極についてのベクトルの先端は上下左右に動くだけで回転角度は0である。式(1)は、これらのベクトルの乗除算で得られるベクトル値なので、\(L\)に沿っての\(s\)の変化に対して\(1+G(s)H(s)\)の先端の軌跡、すなわちベクトル軌跡は原点の周りを時計方向に1回転する。
例えば、\(s_1=0.5 , \; p_1=-1.5\)としたときの\(1+G(s)H(s)\)のベクトル軌跡は、図3のようになる。特性根は複素平面の右半平面にあり、極は左半平面にある。このときのベクトル軌跡は、原点の周りを時計方向に1回転することになる。
不安定特性根1個
\(s_1=0.5,\; s_2=2.0, \; p_1=-1.5, \; p_2=-2.0\)のように特性根が複素平面の右半平面に2個(つまり不安定な特性根が2個)あり、極が左半平面にある場合、このときのベクトル軌跡は、図4に示すように、原点の周りを時計方向に2回転することになる。
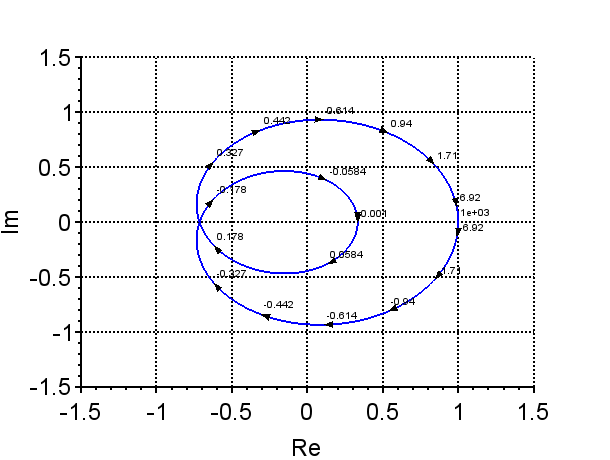
不安定特性根2個
ここで、\(s_1=0.5,\; s_2=2.0, \; p_1=-1.5, \; p_3=0.7\)のように特性根が複素平面の右半平面に2個あり、極が右半平面に1個ある場合、つまり、経路\(L\)内に極\(p_3\)があるとき、極\(p_3\)によるベクトル\(s-p_3\)の回転角度も時計方向に\(2\pi\)となる。しかし、\(s-p_3\)は式(1)の分母側にあるので、これによる\(1+G(s)H(s)\)のベクトルの回転の寄与分は\(s-s_1, \; s-s_2\)と逆に反時計方向に\(2\pi\)である。従って、全体としての\(1+G(s)H(s)\)のベクトル軌跡は、図5に示すように、原点の周りを時計方向に1回転することになる。
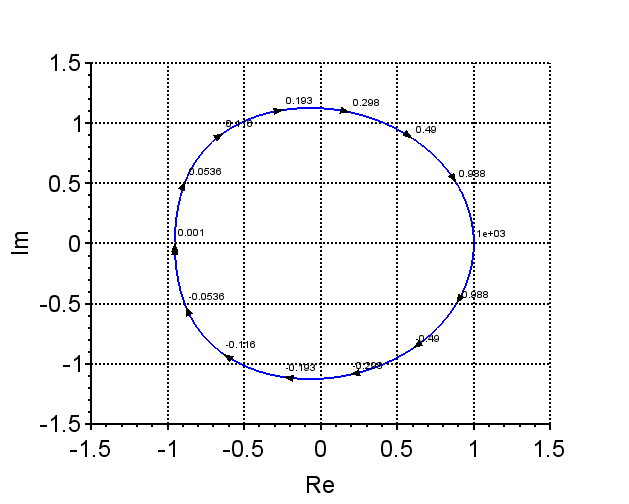
不安定特性根2個と不安定極1個
また、\(s_3=-0.5,\; s_4=-1.0, \; p_1=-1.5, \; p_2=-2.0\)のように特性根が複素平面の左半平面に2個(つまり不安定な特性根が無い)で、極が左半平面に2個の場合、ベクトル軌跡は、図6に示すように、原点から右側で回転することになる。
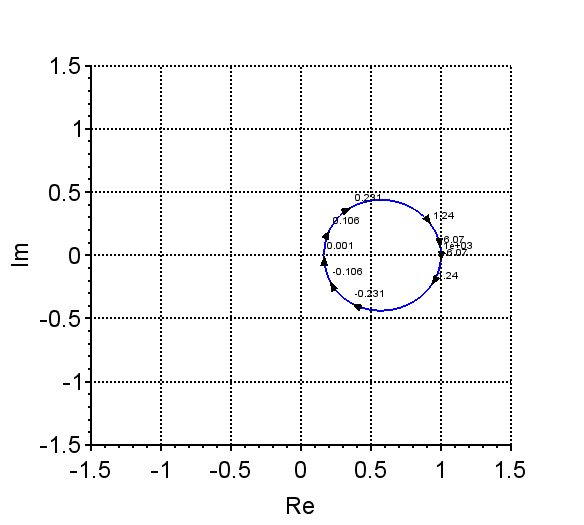
不安定根が無い場合
以上のことから次のようにいえる。もし\(s\)平面上で時計方向の閉経路\(L\)の中の特性根の数を\(R\)個、\(1+G(s)H(s)\)の極つまり\(G(s)H(s)\)の極の数を\(P\)個、\(1+G(s)H(s)\)のベクトル軌跡の原点まわり時計方向の回転数を\(N\)とすると、\(R=N+P\)の関係がある。\(s\)平面上の時計方向の閉経路\(L\)を複素平面の虚軸の右半平面をおおうように広げると(\(L_{\infty}\)とすると)、不安定根は必ずこの中に含まれることになる。従って、この\(R\)は不安定根の数になる。これが0のときに限ってシステムは安定であることになる。
閉経路\(L_{\infty}\)に対する\(1+G(s)H(s)\)のベクトル軌跡において、\(G(s)H(s)\)は一般に有理関数であり、分母の次数が分子の次数より高いので、閉経路\(L_{\infty}\)の無限大の半径の部分(\(s\)の実部が正の領域)においては、\(1+G(s)H(s)=1\)となる。従って、\(1+G(s)H(s)\)の軌跡は虚軸上の\(s\)の値、つまり、\(s=j\omega , \;\;\; -\infty \lt \omega \lt \infty\)の範囲で描けばよい。
特性方程式のベクトル軌跡とナイキスト軌跡
特性方程式のベクトル軌跡とナイキスト軌跡の関係を具体的な伝達関数から見る。$$G(s)=\frac{4}{s^2+2s+2} , \;\;\;\ H(s)=1$$とする。このとき、特性方程式は$$1+G(s)H(s)=0$$であり、開ループ伝達関数は$$L(s)=G(s)H(s)$$である。また、閉ループ伝達関数は、$$T(s)=\frac{G(s)}{1+G(s)H(s)}$$である。
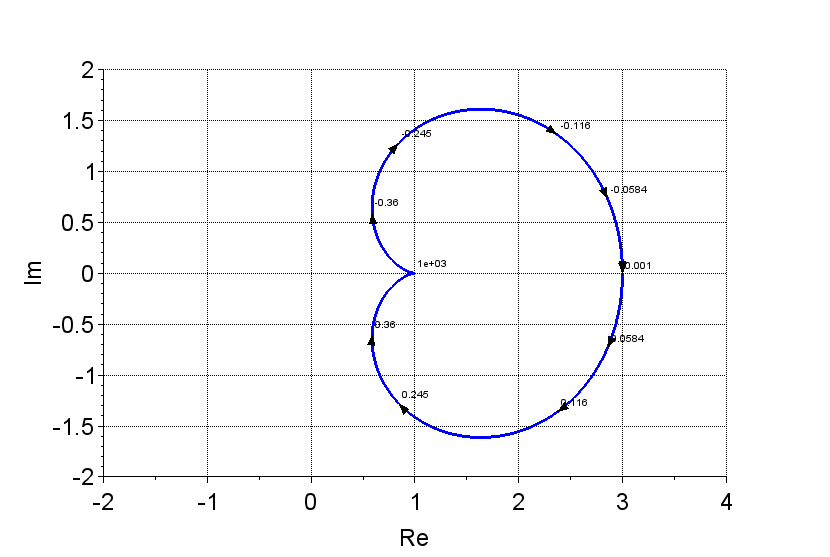
のベクトル軌跡
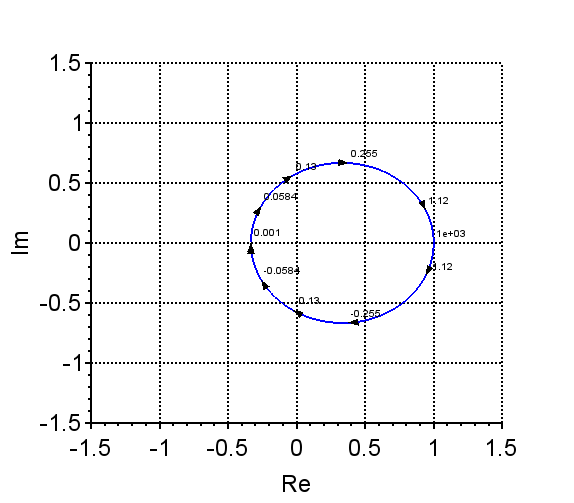
特性方程式のベクトル軌跡は、\(s=j\omega , \;\;\; -\infty \lt \omega \lt \infty \)の範囲で描けばよいので、\(1+G(j\omega)H(j \omega)\)のベクトル軌跡を描くと、図7のようになる。このベクトル軌跡は、原点0のまわりを回転していないので、\(N=0\)である。また、\(G(s)H(s)\)の極は複素平面の右半平面にないので、\(P=0\)である。よって、不安定根\(R=0\)であり、このシステム\(T(s)\)は安定である。
以上は、\(1+G(j\omega)H(j \omega)\)のベクトル軌跡で考えたが、開ループ伝達関数\(G(s)H(s)\)において、\(s=j \omega\)として\(G(j \omega)H(j \omega) \)のベクトル軌跡を描くと図8のようになる。これは、\(1+G(j\omega)H(j \omega)\)のベクトル軌跡を\(-1\)だけ平行移動したものである。したがって、原点まわりの\(1+G(j\omega)H(j \omega)\)の軌跡の回転数\(N\)は、この場合、\(-1+j0\)の点のまわりの回転数を\(N\)と考えれば良い。
この\(G(j \omega)H(j \omega) \)のベクトル軌跡をナイキスト軌跡とよぶ。
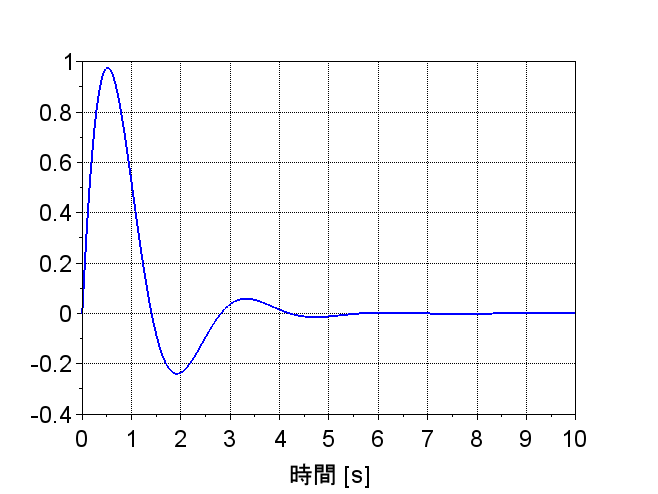
なお、このシステム\(T(s)\)のインパルス応答は、図9のようになり、このシステムが安定であることがわかる。
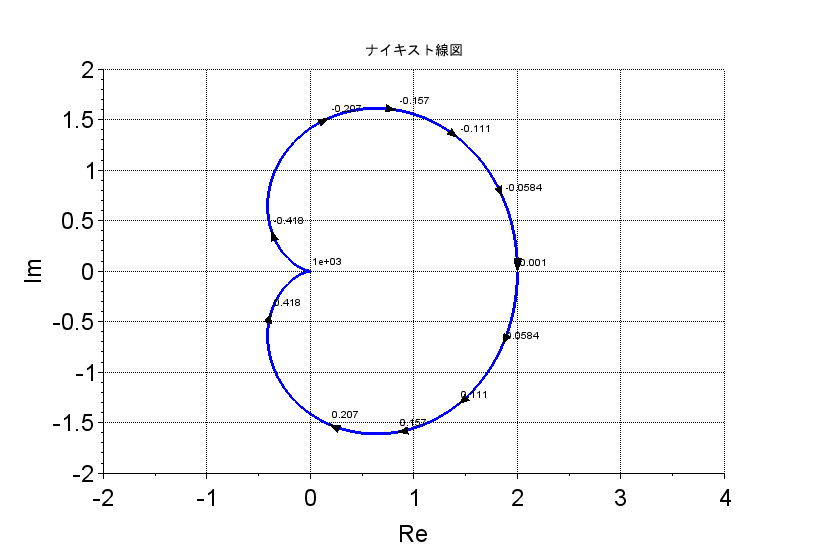
のナイキスト軌跡