16. オブザーバの設計
オブザーバの設計では、オブザーバの極配置を実現するためのオブザーバゲインを決定することが主要な問題となる。オブザーバの極は、オブザーバが推定するシステム内部の状態量が収束する速度を決定するためのパラメータであり、極が適切に設定されていない場合、オブザーバが不安定になり、オブザーバを使ったフィードバックシステムの制御が失われる可能性がある。
一般的には、オブザーバの極配置は、状態フィードバックの極配置と同様に、複素平面上の位置で表される。極が左半面にある場合、オブザーバは安定であり、状態量の推定誤差は指数的に減衰し零に収束する。一方、極が右半面にある場合、オブザーバは不安定であり、推定誤差は指数的に増大する。
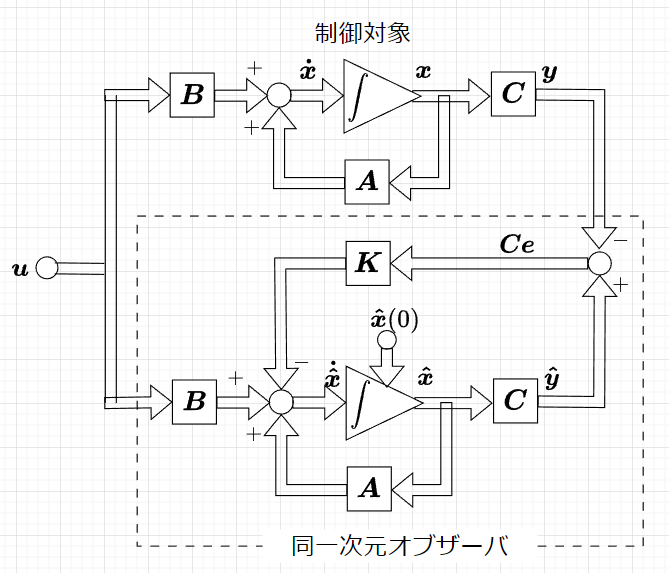
図「同一次元オブザーバ」を基に、オブザーバゲインの決定について考える。制御対象は\(n\) 次元\(m\) 入力 1出力線形時不変システム、$$\boldsymbol{\dot{x}} = \boldsymbol{Bx + Bu} \;\;\;\;\;\;\; \boldsymbol{y} = \boldsymbol{cx}$$とする。このシステムが可観測であれば、変換行列\(\boldsymbol{T}_o \;\; (\boldsymbol{\tilde{x}} = \boldsymbol{T}_o \boldsymbol{x})\)を$$\boldsymbol{T}_o = \boldsymbol{LM}_o \\ \boldsymbol{L} = \begin{bmatrix} a_1 & a_2 & \cdots & a_{n-1} & 1 \\a_2 & a_3 & \cdots & 1 & 0 \\ \vdots & \vdots & \boldsymbol{1} & \vdots & \vdots \\ a_{n-1} & 1 & \cdots & 0 & \vdots \\1 & 0 & \cdots & \cdots & 0 \end{bmatrix} ,\;\;\;\; \boldsymbol{M}_o= \begin{bmatrix} \boldsymbol{c} \\ \boldsymbol{cA} \\ \vdots \\ \boldsymbol{cA}^{n-2} \\ \boldsymbol{cA}^{n-1} \end{bmatrix}$$によって、 $$\boldsymbol{\dot{\tilde{x}}} = \boldsymbol{A}_o \boldsymbol{\tilde{x}} + \boldsymbol{B}_o \boldsymbol{u} \\ y = \boldsymbol{c}_o \boldsymbol{\tilde{x}}$$ $$\boldsymbol{A}_o = \boldsymbol{T}_o \boldsymbol{AT}_o^{-1} = \begin{bmatrix} 0 & 0 & \cdots & 0 & -a_0 \\ 1 & 0 & \ddots &\vdots & -a_1 \\0 & 1 & \ddots & \vdots & -a_2 \\ \vdots & \ddots & \ddots & 0 & \vdots \\ 0 & \cdots & 0 & 1 & -a_{n-1} \end{bmatrix}, \;\;\;\;\;\; \boldsymbol{B}_o = \boldsymbol{T}_o \boldsymbol{B} \\ \boldsymbol{c}_o = \boldsymbol{cT}_o^{-1} = \begin{bmatrix} 0 & 0 & \cdots & 0 & 1 \end{bmatrix}$$と可観測正準形に変換できる。\(a_0, \; a_1,\; \cdots, \; a_{n-1}\)は制御対象の特性方程式$$|s \boldsymbol{I - A} | = s^n +a_{n-1} s^{n-1} + \cdots + a_1 s + a_0 = 0$$の係数である。この可観測正準形にオブザーバゲイン\(\boldsymbol{k}_o = \begin{bmatrix} k_{o1} & k_{o2} & \cdots & k_{on} \end{bmatrix}^T\)とする同一次元オブザーバを構成する。$$\boldsymbol{\dot{\hat{\tilde{x}}}} = \boldsymbol{A}_o \boldsymbol{\hat{\tilde{x}}} + \boldsymbol{B}_o \boldsymbol{u} + \boldsymbol{k} _o (\hat{y} - y) \\ \hat{y} = \boldsymbol{c}_o \boldsymbol{\hat{\tilde{x}}}$$これより、推定誤差は、$$\boldsymbol{e} = \boldsymbol{\hat{\tilde{x}}} - \boldsymbol{\tilde{x}} $$であり、$$\boldsymbol{\dot{e}} = \boldsymbol{\dot{\hat{\tilde{x}}}} - \boldsymbol{\dot{\tilde{x}}} = \boldsymbol{A}_o \boldsymbol{\hat{\tilde{x}}} + \boldsymbol{B}_o \boldsymbol{u} + \boldsymbol{k}_o (\boldsymbol{c}_o \boldsymbol{\hat{\tilde{x}}} - \boldsymbol{c}_o \boldsymbol{\tilde{x}} ) - (\boldsymbol{A}_o \boldsymbol{\tilde{x}} + \boldsymbol{B}_o \boldsymbol{u})\\= (\boldsymbol{A}_o - \boldsymbol{k}_o \boldsymbol{c}_o) \boldsymbol{e}$$となる。この特性方程式は、$$|s \boldsymbol{I} - \boldsymbol{A}_o + \boldsymbol{k}_o \boldsymbol{c}_o| = \begin{bmatrix} s & 0 & \cdots & 0 & a_0 + k_{o1} \\ -1 & s & \ddots & \vdots & a_1 + k_{o2} \\ 0 & -1 & \ddots & \vdots &a_2 + k_{o3} \\ \vdots & \ddots & \ddots & s &\vdots \\ 0 & \cdots & 0 & -1 & s + a_{n-1} + k_{on} \end{bmatrix} \\= s^n + (a_{n-1} + k_{on})s^{n-1} + \cdots +(a_2 + k_{o3})s^2 + (a_1 + k_{o2})s + a_0 + k_{o1} = 0 \;\; \cdots (1)$$となる。配置したい極を\(\lambda_1, \; \lambda_2, \; \cdots, \; \lambda_n\)とすると、特性方程式は、$$(s - \lambda_1)(s - \lambda_2) \cdots (s - \lambda_n) = 0$$となる。従って、この特性方程式を展開して、式(1)の係数と比較すれば、可観測正準形のオブザーバゲイン \(\boldsymbol{k}_o = \begin{bmatrix} k_{o1} & k_{o2} & \cdots & k_{on} \end{bmatrix}^T\)を求められる。この可観測正準形のオブザーバゲイン\(\boldsymbol{k}_o\)から、もとの制御対象のオブザーバゲインは、$$\boldsymbol{g} = \boldsymbol{T}_o^{-1} \boldsymbol{g}_o$$と計算できる。
同一次元オブザーバの設計【例】
以下の制御対象の同一次元オブザーバを設計する。$$\boldsymbol{\dot{x}} = \boldsymbol{Ax + Bu} \\=\begin{bmatrix} 0 & 1 \\ -1 & -2 \end{bmatrix} \boldsymbol{x} + \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\boldsymbol{u} \\ y =\boldsymbol{cx} = \begin{bmatrix} 1 & 0 \end{bmatrix} \boldsymbol{x}$$オブザーバの極を\(\lambda_1 = -5 , \;\; \lambda_2 = -6\)とする。
Scilabでの計算結果
--> Ob //可観測行列
Ob =
1. 0.
2. 1.
--> n //ランク
n =2
--> k //オブザーバゲイン
k =
9.
11.
--> A2
A2 =
-9. 1.
-12. -2.
以上の計算結果より、以下の同一次元オブザーバが得られる。
なお、同一次元オブザーバの構造に以下の式を使う。$$\boldsymbol{\dot{\hat{x}}}(t) = (\boldsymbol{A - KC}) \boldsymbol{\hat{x}} (t)+ \boldsymbol{Ky}(t) + \boldsymbol{B u}(t)$$よって、
$$\boldsymbol{\dot{\hat{x}}} = \begin{bmatrix} -9 & 1 \\ -12 & -2 \end{bmatrix}\boldsymbol{\hat{x}} + \begin{bmatrix} 9 \\ 11 \end{bmatrix} y + \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\boldsymbol{u}$$
Scilabスクリプト【例】
//同一次元オブザーバ
clear;clf();
i=%i;
//制御対象システムの定義
A=[0 1; -1 -2];
B=[1 0; 0 1];
c=[1 0];
sysP=syslin('c',A,B,c);
//制御対象の固有値
evals=spec(A);
//可観測性のチェック
Ob=obsv_mat(A,c);
n=rank(Ob);
//極配置
poles=[-5 -6];
//オブザーバゲインの決定
k= ppol(A',c',poles);
k=k';
//オブザーバのA行列
A2=(A-k*c);

