16. テブナンの定理
テブナンの定理(Thevenin's theorem)とは、線形回路において、ある部分回路を単一の電圧源とその内部抵抗に置き換えることができるという定理で、複雑な回路の解析を簡単にするために使用される。
テブナンの定理
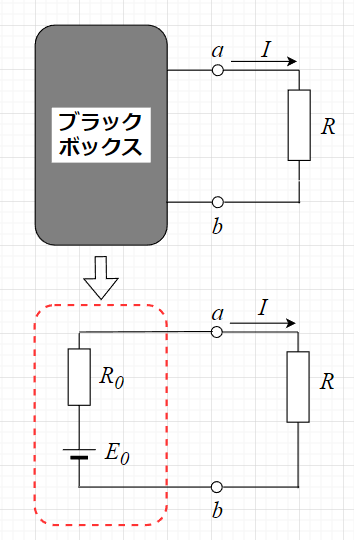
図「テブナンの定理」で”ブラックボックス”部分は、電源を含めた複雑な回路網である。この部分を単一の電圧源と内部抵抗に置き換えることを考える。
まず、電流\(I\)を求めたい部分、この図の場合、端子\(a,b\)のところでブラックボックス部分を切り離す。このときの\(a-b\)間の電圧\(V_{ab}\)は、ブラックボックス内の等価電圧源の起電力\(E_0\)となる。つまり、電流\(I\)が流れないので、電圧降下が生じず\(V_{ab}\)は起電力\(E_0\)そのものとなる。
次に等価抵抗\(R_0\)を求める。このときは、ブラックボックス内部の電圧源は全て短絡、電流源は全て開放にする。これにより、端子\(a-b\)から見た内部抵抗\(R_0\)が求まる。以上により、下図の等価回路が求まる。この図より、求めたい電流\(I\)は、$$I=\frac{E_0}{R_0 +R}$$となる。
このようにテブナンの定理を使えば、回路網の任意の場所の電流を求めることができる。
テブナンの定理の使用【例】
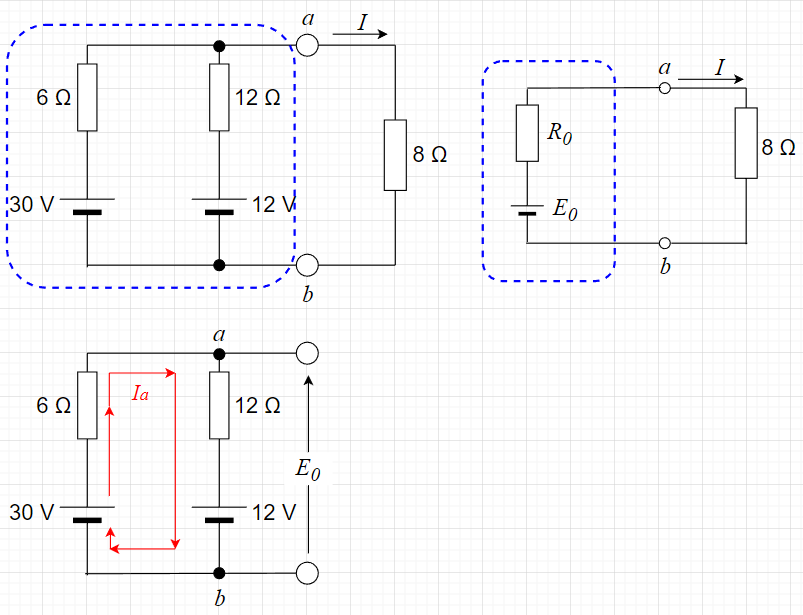
図「テブナンの定理の使用例」で、左上図の青破線で囲んだ部分を\(R_0, E_0\)の等価回路に置き換えて、負荷抵抗(\(8\;\Omega\))に流れる電流\(I\)を求める。
まず、端子\(a,b\)で青破線で囲んだ回路を切り離す。このとき、下図のようになるため、電圧が高い\(30 \; V\)の電圧源から電圧が低い\(12 \; V\)の電圧源に向かって電流\(I_a\)が流れる。このとき、抵抗\(6 \; \Omega\)と抵抗\(12 \; \Omega\)は直列接続になる。よって、電流\(I_a\)は$$I_a = \frac{30-12}{6 + 12} = 1 \; A$$となる。また、\(a\)点の電圧は、\(30 \; V\)の電圧源から\(6 \; \Omega\)による電圧降下で、\(30 - 6 \times 1 = 24 \; V\)となる。よって、等価回路の\(E_0\)は\(E_0 = 24\; V\)である。
次に、電圧源\(30 \; V\)と\(12 \; V\)を短絡して、\(a-b\)間の抵抗\(R_0\)を求める。抵抗\(6 \; \Omega\)と抵抗\(12 \; \Omega\)は\(a-b\)間で並列接続になるので、$$R_0 = \frac{6 \times 12}{6 + 12} = 4 \; \Omega$$となる。
\(E_0 = 24 \; V\)、\(R_0 = 4 \; \Omega\)なので、電流\(I\)は、$$ I= \frac{E_0}{R_0 + R}= \frac{24}{4 + 8} = 2 \; A$$と求まる。
参考:キルヒホッフの法則での解析
図「テブナンの定理の使用例」と同じ回路をキルヒホッフの法則を使って解析する。
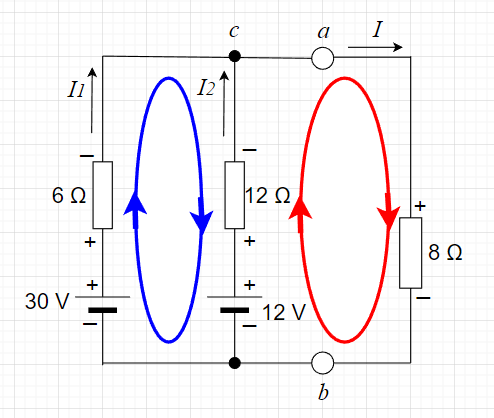
図「キルヒホッフの法則での解析」のように、電流\(I_1 , I_2 , I\)の方向を仮定する。
\(c\)点において、KCLより、$$I_1 + I_2 =I$$青線のループにおいて、KVLより、$$30 - 6\times I_1 + 12 \times I_2 - 12 = 0$$ 赤線のループにおいて、KVLより、$$12 - 12 \times I_2 - 8 \times I = 0$$ よって、$$I_1 + I_2 - I=0 \\ 6 I_1 - 12 I_2 = 18 \\ 12 I_2 + 8 I = 12 $$この3元連立方程式を解くと、$$I_1 = \frac{7}{3} \;A \\ I_2 = -\frac{1}{3} \; A \\ I = 2 \;A$$となる。
当然であるが、\(I = 2 \; A\) とテブナンの定理を使った時と同じ結果が得られる。
実際の回路網は、このように単純なことは少ない。つまり、端子\(a-b\)の左側の回路部分(ブラックボックス)は、実際には複雑であるため、キルヒホッフの法則での解析は複雑になる。もっとも、回路シミュレータを使えば、複雑な回路網であっても、コンピュータによって解析できるし、その手法が実用的であると考える。
ただし、コンピュータを使用した回路解析を適切に実施する上で、キルヒホッフの法則やテブナンの定理などの原理、アルゴリズムを理解しておくことが重要である。


“16. テブナンの定理” に対して1件のコメントがあります。
コメントは受け付けていません。