11. 直流の測定原理
直流電流を測定する場合は、電流計は負荷に直列に接続する。また、電圧計は、負荷に並列に接続する。
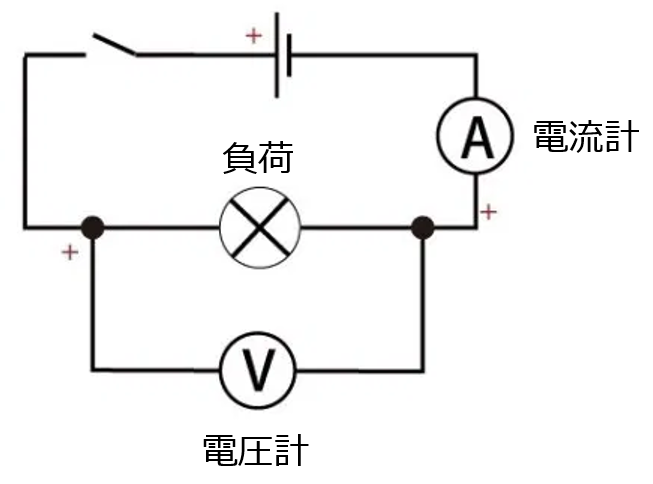
テスタによる電流測定方法
テスタで電流を測定する場合は、電源をOFFにして、回路を切断する必要がある。テスタを回路中に挿入して、その後、電源をONにして測定する。
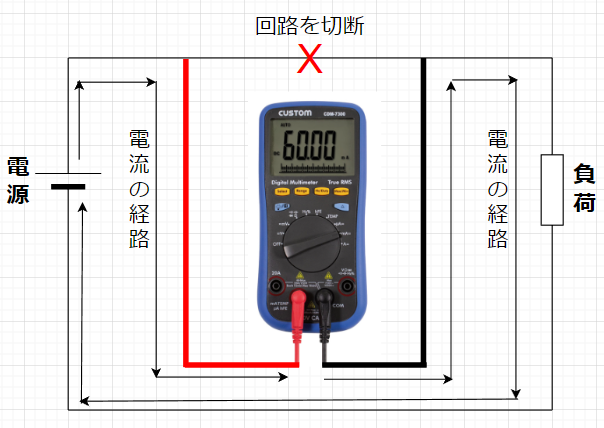
永久磁石可動コイル形計器
直流を測る基本的な計器として、永久磁石可動コイル形計器がある。
永久磁石可動コイル形の測定器は、コイルが、磁場の中で自由に回転することで動作する。この磁場は永久磁石によって生成する。測定器に通された電流は、回転するコイル内に電流が流れるため、コイルを取り巻く磁場で影響を受ける。電流が流れていない場合、コイルは磁場に対して回転しない。コイルに電流が流れると、コイルに働く力が変化し、コイルは磁場に対して回転する。この原理は、ファラデーの電磁誘導の法則に基づいている。
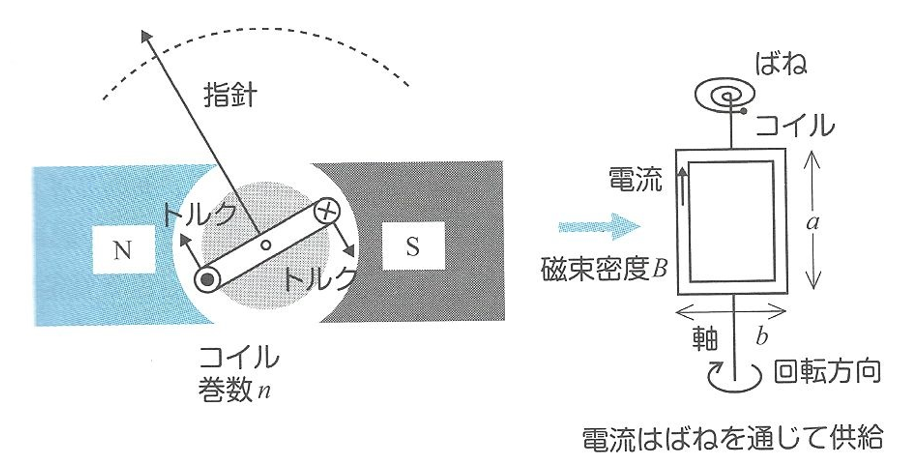
磁束密度 \(B\)[T] , コイルの高さ \(a\)[m]
コイルの幅 \(b\)[m] , コイル巻き数 \(n\)
電流 \(I\)[A] , 発生トルク \(\tau\)[Nm]

・指針の運動方程式
振れ角 \(\theta\)[rad]
可動部の慣性モーメント \(J\)[kg・m2]
制動定数 \(D\) [N・m/(rad/s)]
ばね定数 \(K\)[N・m/rad] として、指針の運動方程式は、$$J\frac{d^2 \theta}{dt^2} +D\frac{d\theta}{dt} + K\theta = \tau$$となる。この方程式から、制動定数、ばね定数等の設計値が決定できる。
微小電流の計測
永久磁石可動コイル形は、ファラデーの電磁誘導を直接利用した単純な構造で、高感度に実装でき、\(nA\)( \(10^{-9} \;A\))程度の測定が可能である。なお、検流計は電流の検出に特化した高感度に設計した電流計である。

検流計より高感度を必要とする場合は、低ノイズ電流アンプを使用して、電流信号を増幅する。
ゲイン 最大 \(10^{13}\) V/A 程度のものがある。これであれば、\(pA\) (\(10^{-12} \;A\))以下の電流測定ができる。
測定範囲の拡大
大電流を測るには、電流計に並列に抵抗をつなぎ測定対象の電流をこの抵抗\(R\)に分流して測定電流の範囲拡大を行う。
$$R I_R = R(I - I_m) = R_m I_m$$
よって、測定したい電流\(I\)は、$$I= \frac{R + R_m}{R} I_m$$となる。つまり、電流計の内部抵抗\(R_m\)とシャント抵抗\(R\)の抵抗値が分かっていれば、電流計で測定された電流\(I_m\)から測定したい電流\(I\)が求まることになる。
使用するシャント抵抗は、測定したい電流\(I\)の概算値から、$$ R=\frac{I_m}{I-I_m }R_m$$と設計できる。
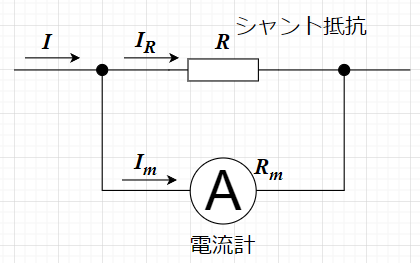
電流測定範囲の拡大
参考(分流の式)
シャント抵抗は、電流の分流を利用している。図「分流」より、分流の式を求める。$$E=R_1 I_1 \;\;\;\; E=R_2 I_2 \\I_1 = \frac{E}{R_1} \;\;\;\; I_2 = \frac{E}{R_2}$$
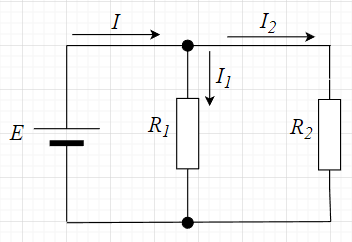
$$I=I_1 + I_2 =\left(\frac{1}{R_1} + \frac{1}{R_2} \right)E =\left(\frac{R_1 + R_2}{R_1 R_2} \right)E$$ $$E = \left( \frac{R_1 R_2}{R_1 + R_2}\right)I$$ $$I_1 = \left( \frac{R_1 R_2}{R_1 + R_2}\right)I \times \frac{1}{R_1} = \frac{R_2}{R_1 + R_2} I$$ $$I_2= \left( \frac{R_1 R_2}{R_1 + R_2}\right)I \times \frac{1}{R_2} = \frac{R_1}{R_1 + R_2} I$$ また、$$I = \frac{R_1 + R_2}{R_2}I_1 \\ =\frac{R_1 + R_2}{R_1}I_2$$となる。


“11. 直流の測定原理” に対して2件のコメントがあります。
コメントは受け付けていません。