5. 離散時間システムの応答
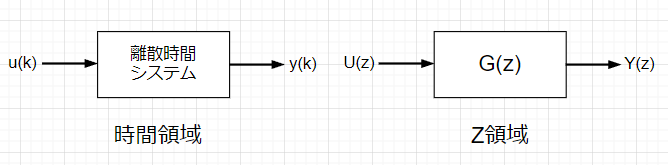
\(u(k)\):入力信号、\(U(z)=\mathcal{Z}\left\{u(k)\right\}\)、 \(y(k)\):出力信号、\(Y(z)=\mathcal{Z}\left\{y(k)\right\}\)
離散時間システムの伝達関数:\(G(z)=\frac{Y(z)}{U(z)}\)
離散時間システムの入出力
1)伝達関数表現による入出力関係
パルス伝達関数を使うと、離散時間システムの入出力関係は、$$Y(z)=G(z)U(z)$$と表される。
2)時間領域での入出力関係
畳み込み演算を使うと、離散時間システムの入出力関係は、\(y(kT)=\sum_{n=0}^k g(nT)u(kT - nT)\)で、\(T\)を省略して$$y(k)=\sum_{n=0}^k g(n)u(k - n)$$と表される。\(g(n)\):離散時間システムのインパルス応答 \(g(n)=\mathcal{Z}^{-1}\left\{G(z)\right\}\)
※畳み込み演算 伝達関数の乗算は、畳み込み和のZ変換になる。$$G(z)U(z)=\mathcal{Z}\left\{\sum_{n=0}^{\infty} g(nT)u(kT-nT)\right\}$$ $$\mathcal{Z}\left\{\sum_{n=0}^\infty g(nT)u(kT -nT)\right\} = \sum_{k=0}^\infty \left\{\sum_{n=0}^{k} g(nT)u(kT - nT)\right\}z^{-k}$$ $$= \sum_{n=0}^\infty \sum_{k=0}^\infty g(nT)u(kT - nT)z^{-k}$$ \(m=k-n\)とおくと$$=\sum_{n=0}^\infty g(nT)z^{-n} \sum_{m=-n}^\infty u(mT)z^{-m}$$ \(t \lt 0\)で\(u(t)=0\)として$$=\sum_{n=0}^\infty g(nT)z^{-n} \sum_{m=0}^\infty u(mT)z^{-m} = G(z)U(z)$$
3)状態方程式による入出力関係
状態変数\(x(k)\)を使って、$$x(k+1) = Ax(k) + bu(k) \;\;\;\;\; y(k)=cx(k)$$と表される。 このとき、伝達関数は$$G(z)=c(zI - A)^{-1}b $$と表される。
インパルス応答
離散時間の単位インパルス(クロネッカーの\(\delta\)関数)は、$$\delta(k)=\begin{cases} 0 \;\;\;\;\; (k \ne 0) \\ 1 \;\;\;\;\; (k = 0) \end{cases}$$なので、単位インパルスを入力\(u(k)\)とした場合、\(U(z)=\mathcal{Z}\left\{\delta(k)\right\}=1\)なので、離散時間システム\(G(z)\)の出力は、$$Y(z)=G(z)U(z)=G(z)\cdot1=G(z)$$となる。従って、出力\(y(k)\)は、\(y(k)=\mathcal{Z}^{-1}\left\{G(z)\right\}\)となる。すなわち、インパルスを入力したときの応答、インパルス応答\(g(k)\)は、$$g(k)=\mathcal{Z}^{-1}\left\{G(z)\right\}$$であり、離散時間システムの伝達関数\(G(z)\)は、$$G(z)=\mathcal{Z}\left\{g(k)\right\}$$である。
状態方程式の解
離散時間システムの状態方程式、$$x(k+1) = Ax(k) + bu(k) \;\;\;\;\; y(k)=cx(k)$$において、(\(k=0,1,2,\cdots\))を逐次代入すると、$$x(1) = Ax(0) + bu(0)$$ $$x(2) = A^2x(0) + Abu(0) +bu(1)$$ $$\vdots$$ $$x(k) = A^k x(0) + A^{k-1}bu(0) + \cdots +bu(k-1)$$なので、一般解は、$$x(k) = A^{k}x(0) + \sum_{i=0}^{k-1}A^{k-i-1}bu(i)$$となる。初期値\(x(0)=0\)とすると、出力\(y(k)\)は、$$y(k) = \sum_{i=0}^{k-1}cA^{k-i-1}bu(i)$$となる。
*状態方程式からのインパルス応答
入力\(u(i)\)が単位インパルスとすると、出力\(y(k)\)すなわちインパルス応答\( g(k)\)は、$$y(k)=g(k)=cA^{k-1}b \;\;\;\; (k \ge 1)$$となる。
ステップ応答
入力を離散ステップ信号とする。すなわち、\(u(k)= 1 \;\;\;\;\;\; (k=0,1,2,\cdots)\) である。Z変換は、$$U(z)=\frac{z}{z-1}=\frac{1}{1 - z^{-1}}$$である。従って、ステップ応答は、$$Y(z)=G(z)U(z)=\frac{z}{z-1}G(z)$$の逆Z変換で求められる。$$y(k)=\mathcal{Z}^{-1}\left\{\frac{z}{z-1}G(z)\right\}$$また、$$y(k) = \sum_{i=0}^{k-1}cA^{k-i-1}bu(i)$$なので、\(u(i)=1\)を入力すると、$$y(k)=g(1) + g(2) + \cdots +g(k)$$とインパルス応答の和で表される。
Z.O.H.を含む離散化システムのステップ応答
Z.O.H.を含む離散時間システムのパルス伝達関数は、$$G(z) = (1 - z^{-1})\mathcal{Z}\left\{\frac{G(s)}{s}\right\}$$であり、その単位ステップ応答は、$$Y(z)=G(z)\frac{1}{1 - z^{-1}}=\mathcal{Z}\left\{\frac{G(s)}{s}\right\}$$となる。
一方、連続時間システム\(G(s)\)の単位ステップ応答は、$$y(t) = \mathcal{L}^{-1}\left\{\frac{G(s)}{s}\right\}$$である。従って、Z.O.H.を含む離散時間システムのステップ応答は、連続時間システムの単位ステップ応答をサンプルしたものに等しいことになる。
Scilab による時間応答解析
//離散時間システムの応答
clear; clf;
z=%z;e=%e;
T=1;
G1=0.3/(z-0.7);
G2=1/(z-1.0);
G3=1/(z-1.5);
G1z=syslin(T,G1);
G2z=syslin(T,G2);
G3z=syslin(T,G3);
k=0:T:T*15;
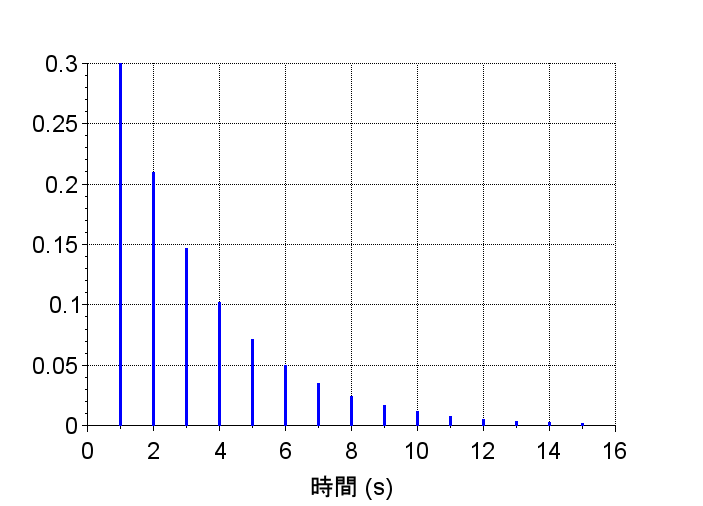
//インパルス応答
u=[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
g1 = flts(u,G1z);
scf(0); plot2d3(k,g1);
g2 = flts(u,G2z);
scf(1); plot2d3(k,g2);
g3 = flts(u,G3z);
scf(2); plot2d3(k,g3);
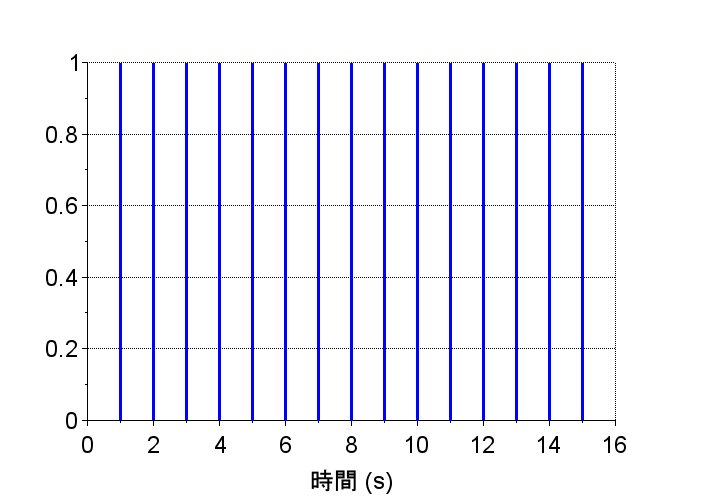
//ステップ応答
u=[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
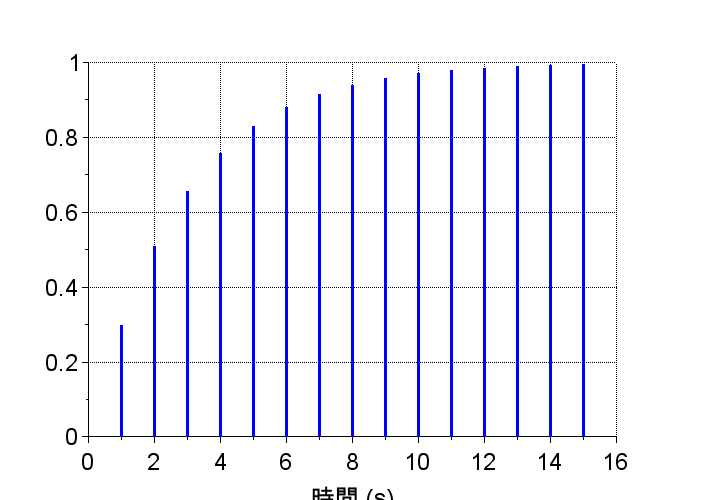
y1 = flts(u,G1z);
scf(3); plot2d3(k,y1);
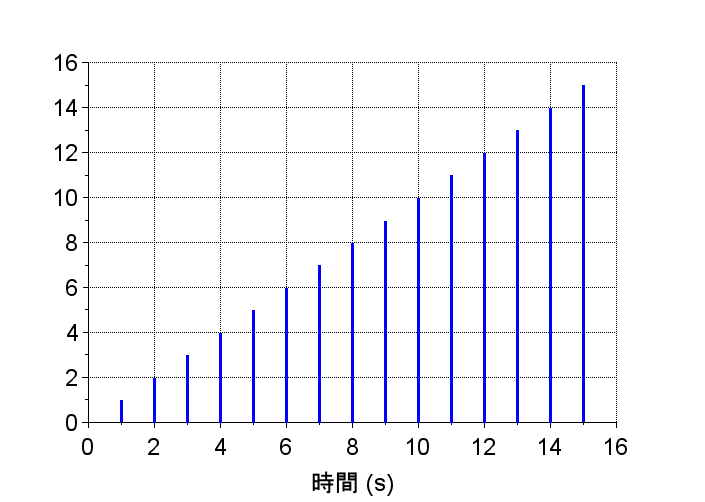
y2 = flts(u,G2z);
scf(4); plot2d3(k,y2);
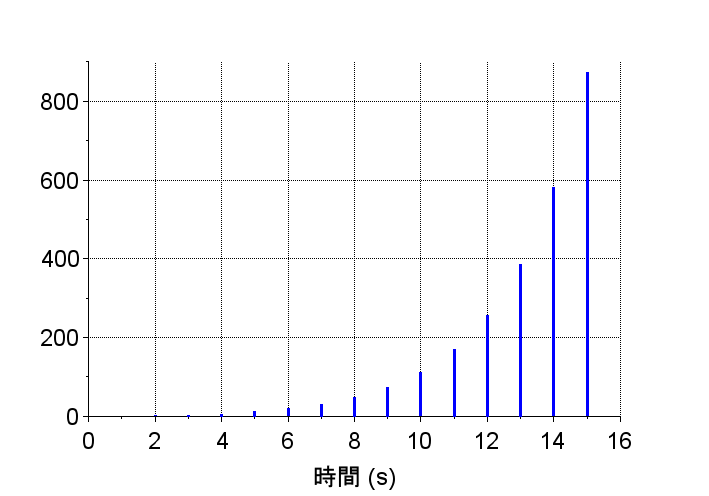
y3 = flts(u,G3z);
scf(5); plot2d3(k,y3);
\(G1(z)\)は極が0.7で単位円内にある。安定なシステムなので、インパルス応答は0に収束している。また、\(G1(z)\)のステップ応答は単位ステップに漸近している。
\(G2(z)\)は極が1.0で単位円上にある。システムは安定限界で、インパルス応答は一定値になっている。また、\(G2(z)\)のステップ応答は直線的に発散している。
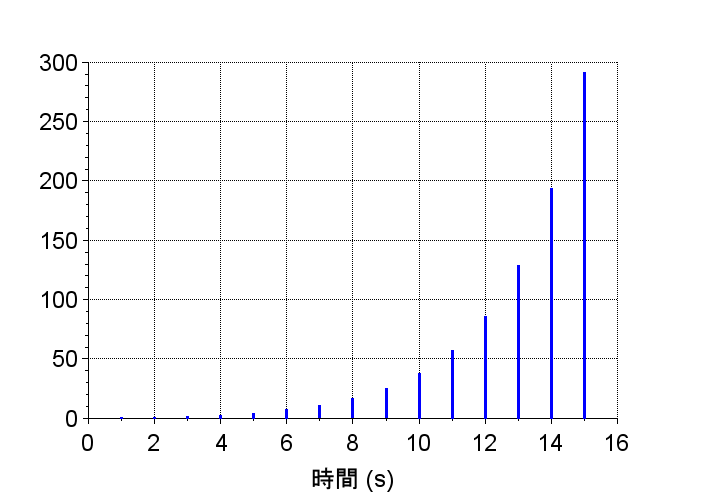
\(G3(z)\)は極が1.5で単位円外にある。システムは不安定で、インパルス応答は指数関数的に発散している。また、\(G3(z)\)のステップ応答は指数関数的に発散している。
※極配置とインパルス応答、安定性の関係については、別項で説明する。


“5. 離散時間システムの応答” に対して1件のコメントがあります。
コメントは受け付けていません。