1. 離散時間制御系の基本事項
連続時間制御系から離散時間制御系へどのように展開していくか、その基本的な考え方を説明する。
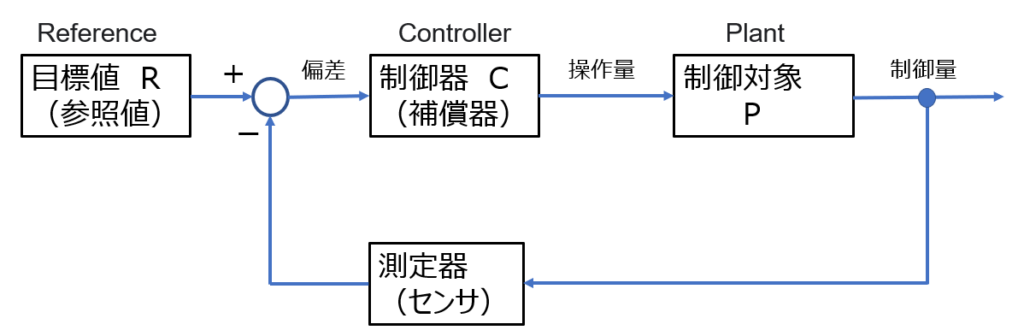
※測定器(センサ)は、制御量を測定し、目標値と同じ量(例えば、電圧)に変換するものなので、制御対象に含めてモデル表現することが多い。
例えば、自動車のタイヤの回転速度はタコメータなどで測定して電圧で出力し、目標値は回転速度ではなくてそれに相当する電圧で与える。
ブロック図「制御系(連続時間系)の基本構成」は、連続時間のフィードバック制御系の基本構成である。離散時間制御系の多くは、このような連続時間制御系の制御器\(C\)の部分をディジタル制御器で実装することを考える。この図では、SISO(1入力1出力)のような表現となっているが、離散時間制御系では、コンピュータ(ディジタル制御器)で実装する利点を活かしMIMO(多入力多出力)も扱えるように状態空間モデルで考えることも多い。
連続時間システムの数学モデル
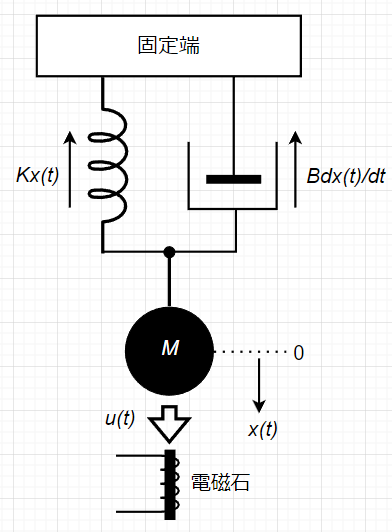
質量・ダンパー・バネで構成されたシステムの数学モデルを考える。このシステムでは、質量\(M\)の鉄球がバネ、ダンパーで支持されており、重力とバネ力が釣り合っている位置\(0\)を起点として、電磁石により鉄球に外力\(u(t)\)を与え、鉄球の変位を制御する。
この微分方程式は、$$M\frac{d^2x(t)}{dt^2} + B\frac{dx(t)}{dt} +Kx(t) = u(t)$$となる。 これを初期値\(0\)でラプラス変換すると、$$Ms^2X(s)+BsX(s)+KX(s)=U(s)$$なので、外力\(u(t)\)から変位\(x(t)\)までの伝達関数は、$$G(s)=\frac{X(s)}{U(s)}=\frac{1}{Ms^2+Bs+K}$$ $$=\frac{\frac{1}{M}}{s^2 + \frac{B}{M}s + \frac{K}{M}}$$となる。
これを状態空間で考えると、状態変数を\(x_1(t)=x(t)\)、\(x_2(t)=v(t)=\frac{dx(t)}{dt}=\frac{dx_1(t)}{dt}\)として、\(\frac{dx_1(t)}{dt}=x_2(t)\)、\(\frac{dx_2(t)}{dt}=-\frac{K}{M}x_1(t) - \frac{B}{M}x_2(t) + \frac{1}{M}u(t)\)となるので、さらに行列を使って表すと、$$\frac{d}{dt}\left[\begin {array}{c c}x_1(t) \\ x_2(t) \end{array}\right]=\left[\begin{array}{c c c} 0 & 1 \\ -a_2 & -a_1 \end {array} \right]\left[\begin{array}{c c}x_1(t) \\ x_2(t)\end{array}\right] + \left[\begin{array}{c c} 0 \\ b\end{array}\right]u(t)$$ (\(a_1 =\frac{B}{M}\)、\(a_2=\frac{K}{M}\)、\(b=\frac{1}{M}\)) となる。これを状態方程式という。また、$$y(t)=\left[\begin{array}{c c}1 & 0\end{array}\right]\left[\begin {array}{c c}x_1(t) \\ x_2(t) \end{array}\right]$$を出力方程式という。
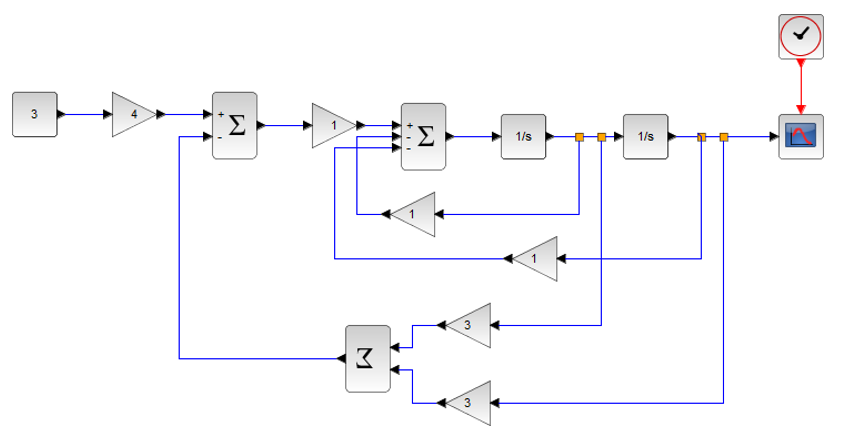
Scilab Xcosでのシミュレーション
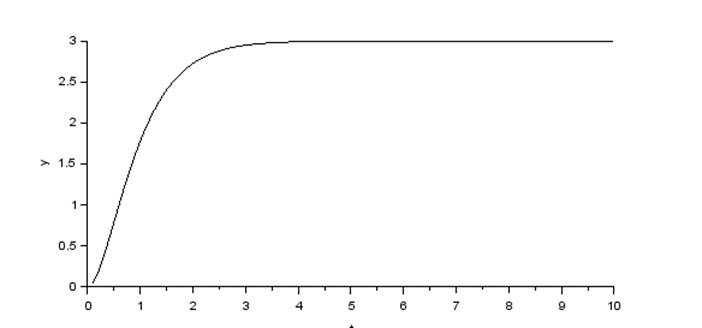
s領域での伝達関数や状態方程式で表現した連続時間制御系に制御器を実装するには、多くの場合コンピュータ(ディジタル制御器)を使用することになる。例えば、図「定位置追従システム(状態フィードバック)」では、各状態変数\(x_1(t)\)、\(x_2(t)\)を測定し、A/D変換器でディジタル量に変換し、コンピュータに入力する。制御演算をした後、D/A変換器でアナログ量に変換して制御対象に操作量を加えることになる。
※A/D変換器(Analog to Digital converter):アナログ量をディジタル量に変換する回路
※D/A変換器(Digital to Analog converter):ディジタル量をアナログ量に変換する回路
(変換器回路に関しては、「電子回路の基礎」で紹介する予定です。)
離散時間システム
ディジタル信号の表現で使う関数
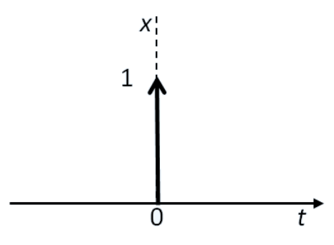
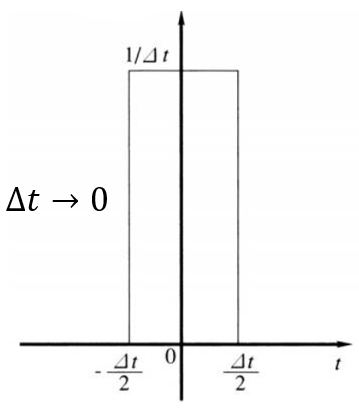
ディジタル信号を表現するのに重要な関数が\(\delta\)関数である。
\(\delta\)関数には以下の2通りの定義がある。クロネッカーの\(\delta\)関数は、離散的な変数に関して用いる。ディラックの\(\delta\)関数は、クロネッカーの\(\delta\)関数の連続変数への拡張となっている。
*クロネッカーの\(\delta\)関数 $$\delta(nT)=\begin{cases} 0 \enspace (n \neq 0) \\ 1 \enspace (n=0) \end{cases}$$*ディラックの\(\delta\)関数 $$\delta(t)=\begin{cases} 0 \enspace \enspace (t \neq 0) \\ \infty \enspace (t=0) \end{cases}$$ $$\int_{-\infty}^{\infty} \delta(t) dt =1 $$
離散時間信号は連続時間信号からサンプリングして生成される。従って、$$f^{*}(t)=\{f(kT)\} \enspace (k=0,1,2,\cdots)$$と表される。\(T\)はサンプリング周期である。連続時間信号\(f(t)\)と\(\delta\)関数を使って表すと、$$f^{*}(t)=\sum_{k=0}^{\infty}f(t)\delta(t-kT)=\{f(0), f(T), f(2T),f(3T),\cdots\}$$となる。
※A/D変換では量子化誤差を考える必要があるが、観測値(制御量)に対して十分な分解能を持ったA/D変換器を使用すれば、基本的に無視できる。最近のA/D変換器は電子回路の高集積化に伴い十分な分解能を持っているので、通常、量子化誤差は考慮しなくて良い。
サンプリング定理
データとして扱うために、連続信号である原信号(元のアナログ信号)から離散的な信号値であるデジタル信号を取り出すことをサンプリングという。サンプリングする周波数をサンプリング周波数という。
サンプリング定理とは、原信号の最大周波数の2倍を超えた周波数でサンプリングすれば原信号を再現できる。
\(f_s\)[Hz]:サンプリング周波数 \(T_s\)[s]:サンプリング周期
\(f_s=\frac{1}{T_s}\) \(\omega = 2\pi f\)[rad/s] (角周波数)
\(f_{max}\) [Hz] :原信号(元のアナログ信号)の最大周波数 $$f_s \gt 2f_{max} \enspace \enspace \omega_ s \gt 2\omega_{max}$$ $$\omega_s =\frac{2\pi}{T_s} \enspace \enspace T_s \lt \frac{\pi}{\omega_{max}}$$ サンプリング周波数は、原信号の最大周波数の2倍を超えた(注:2倍以上ではない)周波数である必要がある。原信号が復元可能な周波数の上限をナイキスト周波数という。
※リアルタイムの制御では、制御帯域の最大周波数より十分に高い周波数(一般的には10倍以上)でサンプリングする必要がある。


“1. 離散時間制御系の基本事項” に対して1件のコメントがあります。
コメントは受け付けていません。