17-2. オペアンプによる非線形回路(2)
オペアンプ(演算増幅器)に非線形素子を付け加えた回路を考える。設計例を基にLTspiceで数値解析を行い、その特性を観察する。
ピーク値検出回路
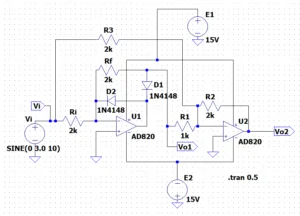
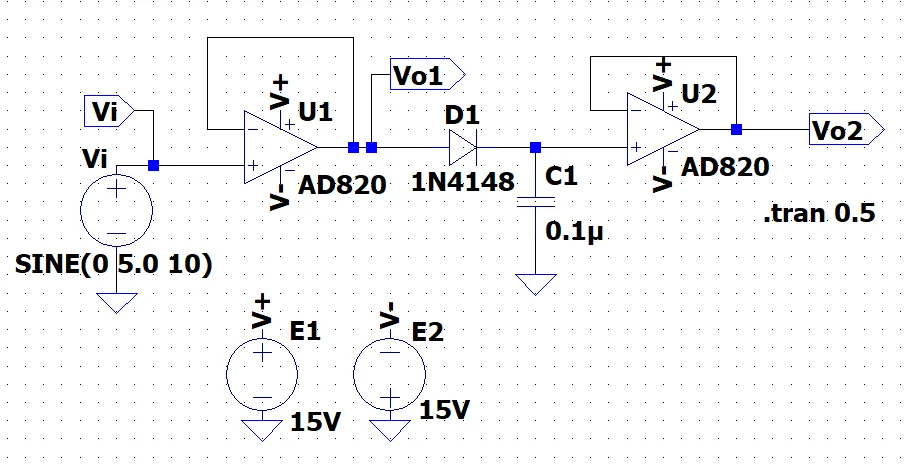
図1にピーク値検出の基本回路を示す。オペアンプに非線形素子のダイオード\(D1\)とキャパシタ\(C1\)を組み合わせることで、正のピーク値電圧(あるいは最大値)を検出する回路ができる。図のオペアンプ\(U2\)はボルテージフォロワとなっている。\(t=0\)で\(C1\)の端子電圧を\(0\;V\)とする。このとき、\(Vo2 = 0 \;V\)である。ある時間\(t1\)で入力電圧\(Vi\)として正の電圧\(Vi = V1\)が加わると、\(Vo1 > 0\)なのでダイオード\(D1\)は導通(ON)し、オペアンプ\(U1\)はボルテージフォロワを構成する。出力\(Vo1=V1\)は\((R_0 + rd)\cdots C1\)の時定数で\(C1\)を充電し、\(C1\)の端子電圧は\(V1\)となる。ただし、\(D1\)の順方向電圧\(V_T\)ほど低下する。ここで、\(R_0\)はボルテージフォロワの出力抵抗、\(rd\)はダイオード\(D1\)の内部抵抗である。
入力電圧\(Vi\)が\(V1\)より低いときは、ダイオード\(D1\)はカットオフ状態(OFF)となり、\(C1\)の端子電圧は\(V1\)のままで、出力\(Vo2 = V1\)である。\(U2\)のボルテージフォロワの入力抵抗は\(\infty\)なので、\(C1\)は\(Vo1\)が低下しない限り放電しない。
シミュレーション結果(LTspice )
※ボルテージフォロワについては、17. 差動増幅器、ボルテージフォロワ、加算器を参照願います。
入力電圧\(Vi\)が\(V1\)より高い電圧になると、ダイオード\(D1\)は導通し、前述と同じ過程で\(C1\)が充電される。このようにして、入力電圧の最大値を出力として取り出すことができる。
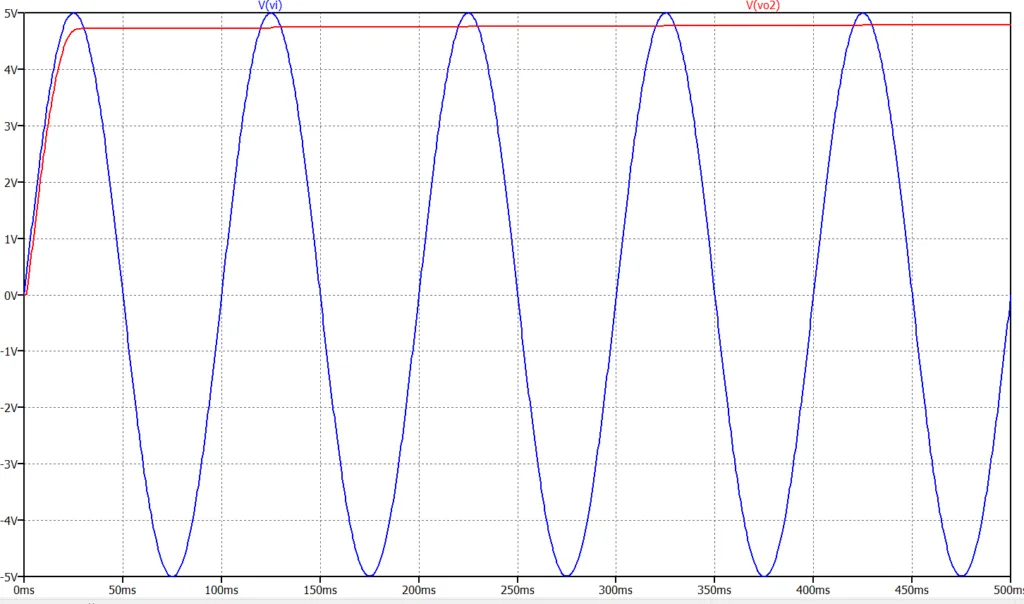
図2がピーク値検出基本回路のシミュレーション結果である。出力\(Vo1\)(赤線)が入力電圧\(Vi\)(青線)の最大値より\(V_T=0.7\;V\)ほど低下していることが分かる。
これを改善した回路例が、下記の記事に掲載されている。
※実用的なピーク値検出回路は、CQ出版社の「正弦波のピーク値を正確に保持できる最大の電圧は?」の記事を参照願います。
サンプル・ホールド回路
図3にサンプル・ホールド基本回路を示す。増幅回路(\(U1,\;U2\))ともボルテージフォロワ回路となっている。前段の出力は\(Vo1=Vi\)となる。コントロール信号\(Vc\)が\(0\)のとき、\(M1\)(NMOS-FET)はカットオフの状態にある。コントロール信号\(Vc\)に高い正のパルス電圧を加えると、\(M1\)が導通し、\((Ro + r_{ds})C\)の時定数で\(C1\)に充電し、\(C1\)の端子電圧は\(Vi\)となる。ここで、\(Ro\)はボルテージフォロワ\(U1\)の出力抵抗、\(r_{ds}\)は\(M1\)が導通しているときのドレイン-ソース間の内部抵抗である。コントロール信号\(Vc\)が再び\(0\)に戻ると、\(M1\)はカットオフとなり前段のボルテージフォロワ\(U1\)と\(C1\)とは切り離され、\(C1\)の電圧\(Vi\)は保持される。
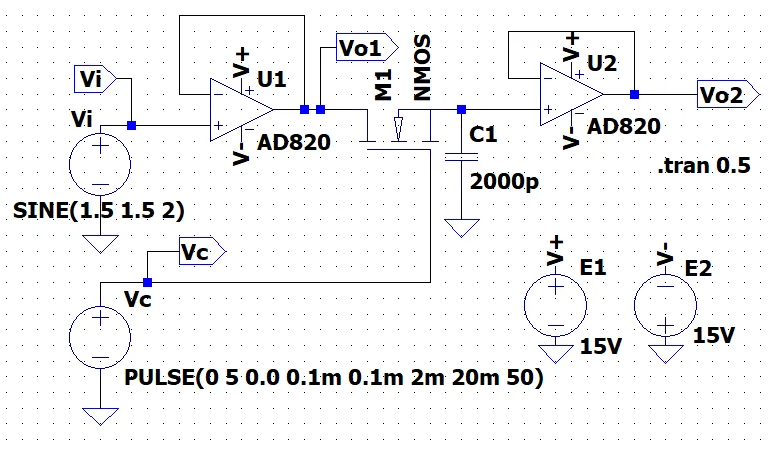
シミュレーション結果(LTspice )
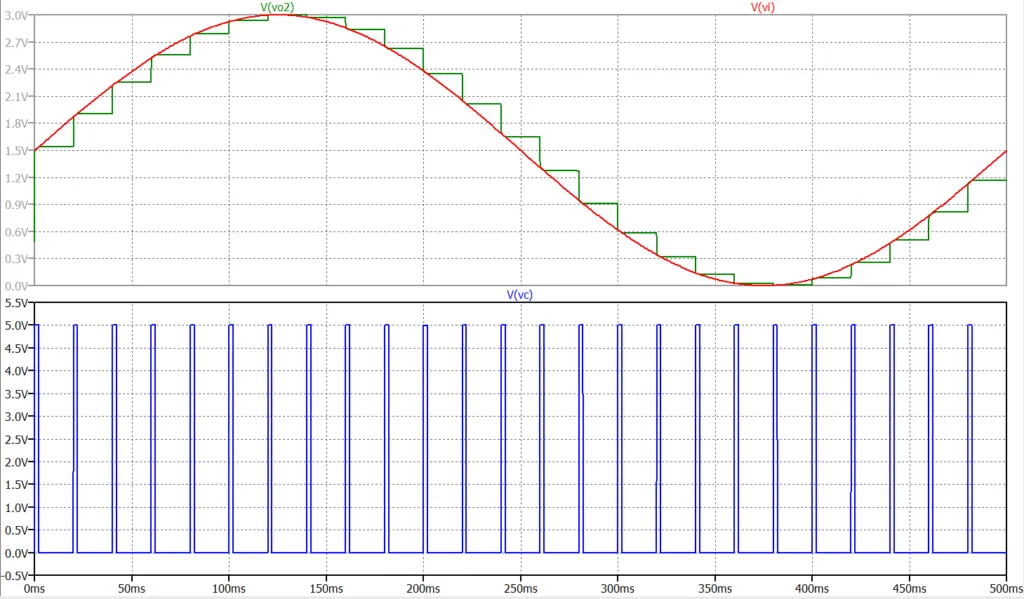
図4がサンプル・ホールド回路基本回路のシミュレーション結果である。出力\(Vo1\)(緑線)は、コントロール信号\(Vc\)(図4の下段)に従って、入力\(Vi\)(赤線)がサンプルされ、保持(ホールド)されていることが分かる。
シュミット・トリガ回路
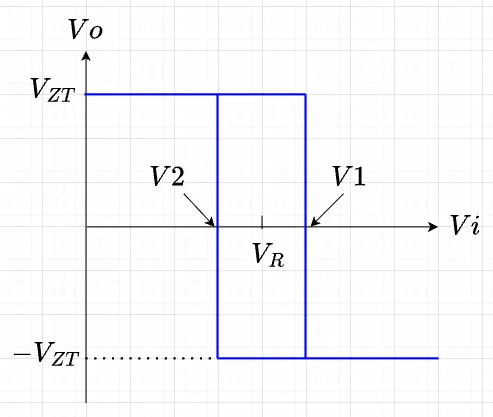
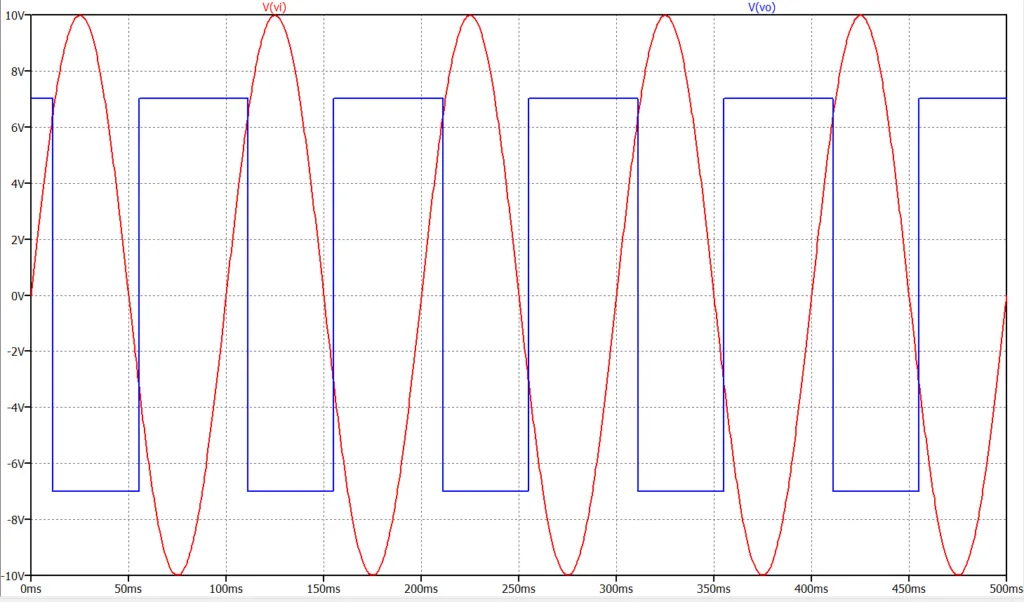
図5にシュミット・トリガ回路を示す。非線形素子としてツェナーダイオード\(Zd1,\;Zd2\)を使用する。出力電圧\(Vo\)が\(Vo = V_Z + V_T\)となっているとする。ここで、\(V_Z\)はツェナー電圧、\(V_T\)はツェナーダイオードの順方向電圧である。\(V_{ZT} = V_Z + V_T\)と表す。\(Vo = V_{ZT}\)のときのオペアンプの入力端子(\(+\))の電圧\(vi2\)は、$$vi2 = V_R + \frac{R2}{R1 + R2}(V_{ZT} - V_R)$$となる。これを\(V1\)とする。オペアンプの利得は十分高いので、バーチャルショートにより、\(vi1 = vi2\)である。従って、\(Vi > V1\)となると、\(Vo = -V_{ZT}\)と変化する。このときの\(vi2\)は、$$vi2 = V_R - \frac{R2}{R1 + R2}(V_{ZT} + V_R)$$となる。これを\(V2\)とする。\(V1 > V2\)なので、さらに\(Vi\)を増加させても、\(Vo = -V_{ZT}\)である。次に、\(Vi\)を減少すると\(Vi > V2\)を満たす範囲では、\(Vo = -V_{ZT}\)である。\(Vi\)をさらに減少し、\(Vi < V2\)の範囲になると、\(Vo = V_{ZT}\)となる。この入出力特性を図6に示す。入力電圧\(Vi\)が\(V1\)以上で出力電圧\(Vo\)は\(-V_{ZT}\)、入力電圧\(Vi\)が\(V2\)以下では出力電圧\(Vo\)は\(V_{ZT}\)となる。
図7はシュミット・トリガ回路の動作シミュレーション結果である。ツェナー電圧\(V_Z = 6.2\;V\)、順方向電圧\(V_T = 0.7 \; V\)なので、\(V_{ZT} = 6.9 \; V\)となり、出力電圧\(Vo\)は\(\pm 6.9\;V\)となる。また、\(V1 = 6.3\;V\)、\(V2 = -2.9\;V\)である。
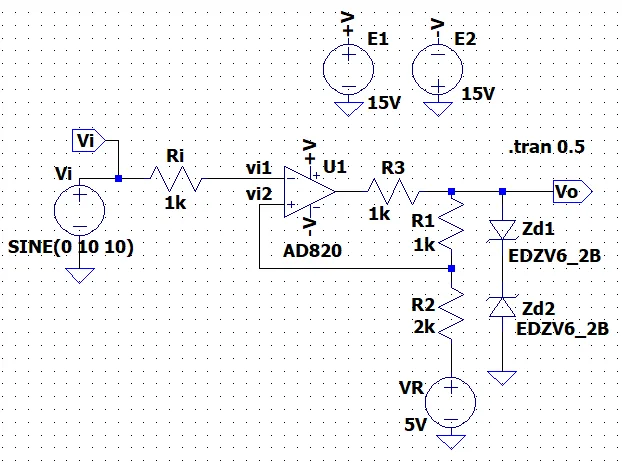
シミュレーション結果(LTspice )