9-1. バイアス回路の解析
電流帰還バイアス回路を使った増幅器を基に、バイアスの最適化についてLTspiceを使って検討する。
※電流帰還バイアスについては、9. BJTのバイアス回路を参照。
バイポーラトランジスタ (BJT) を増幅器として機能させるためには、適切な静止動作点(Q点)を設定する必要がある。最も一般的で安定性の高いバイアス回路である電流帰還バイアス回路を例として、LTspiceでのシミュレーション例を示す。
図1は回路例である。この回路は、\(V_{BE}\)の温度変動\(h_{FE}\) のばらつきに対してロバスト性が高いのが特徴である。
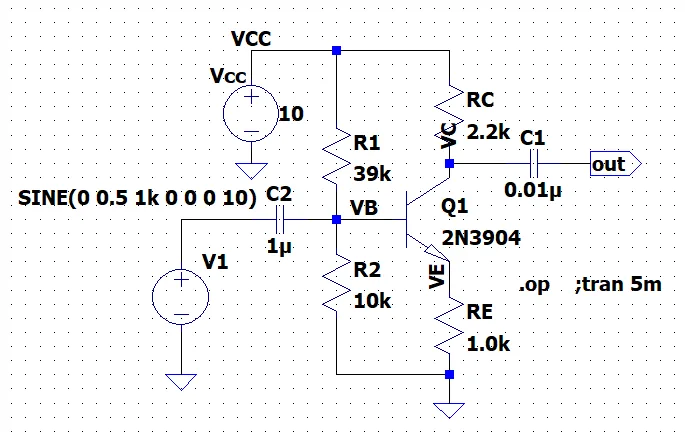
(LTspice)
静止動作点(Q点)の設計値
設定した抵抗値に基づき、Q点の設計値を概算する。
・ベース電圧 (\(V_B\)):\(R1\)と\(R2\)による分圧でベース電圧 \(V_B\)が決まる(ベース電流\(I_B\)を無視できる場合)。$$V_B \approx V_{CC} \cdot \frac{R2}{R1 + R2} = 10\text{ V} \cdot \frac{10\text{ k}\Omega}{39\text{ k}\Omega + 10\text{ k}\Omega} \approx 2.04\text{ V}$$
・エミッタ電流(\(I_E\)):\(V_{BE} \approx 0.7\text{ V}\)と仮定し、エミッタ抵抗\(RE\)にかかる電圧\(V_E = V_B - V_{BE}\)から \(I_E\)を求める。$$V_E = V_B - 0.7\text{ V} \approx 2.04\text{ V} - 0.7\text{ V} = 1.34\text{ V} \\ I_E = \frac{V_E}{RE} = \frac{1.34\text{ V}}{1.0\text{ k}\Omega} \approx 1.34\text{ mA}$$
・コレクタ電圧(\(V_C\)):\(I_C \approx I_E\)と仮定し、\(RC\)での電圧降下を引いて\(V_C\)を求める。$$V_C = V_{CC} - I_C \cdot RC \approx 10\text{ V} - (1.34\text{ mA} \cdot 2.2\text{ k}\Omega) \approx 10\text{ V} - 2.95\text{ V} = 7.05\text{ V}$$
Q点設計値: \(I_C \approx 1.34\text{ mA}, V_{CE} = V_C - V_E \approx 7.05\text{ V} - 1.34\text{ V} = 5.71\text{ V}\)
LTspiceによる解析
LTspiceで静特性(DC特性)を解析するには、動作点解析 (.op) を使用する。.opコマンドは、回路の直流動作点(DC Operating Point)を計算し、すべてのノード電圧と分岐電流を求める。
※メニューバーの Edit から Label Netを選択して、電圧や電流の表示名(ネット名)を設定すると動作点や波形ビューアでの表示が見やすくなる。
.op コマンドをディレクティブとして回路図上に配置し、シミュレーションを実行すると図2に示すようにすべてのノード電圧、各素子の電流が記録されたウィンドウが表示される。
\(V_B\)の設計値\(2.04\;V\)に対し、\(V(vb)\)は、\(2.00684\;V\)である。\(V_{CE}\)の設計値\(5.71\;V\)に対し、\(V_{CE} = V(vc) - V(ve) = 5.70508 \; V\)である。\(I_C\)の設計値\(1.34 \; mA\)に対し、\(I_C(Q1) = 1.34083\;mA\)である。
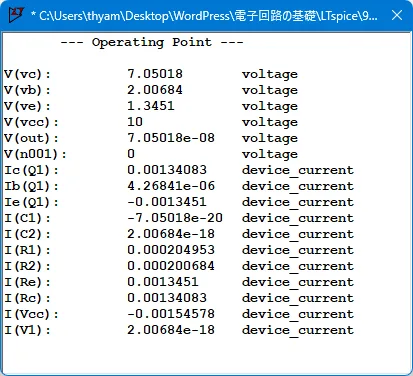
前述の設計値との差は主にトランジスタモデルの各パラメータを設計値では考慮していないことにある。ただし、実際のトランジスタはパラメータに変動(バラツキ)があるため、トランジスタモデルのパラメータを考慮した設計値は通常必要ない。詳細な設計をする場合には、シミュレーションツールを使用し、以下のようなパラメータ変動を考慮した設計をすればよい。
温度特性のシミュレーション(安定性の評価)
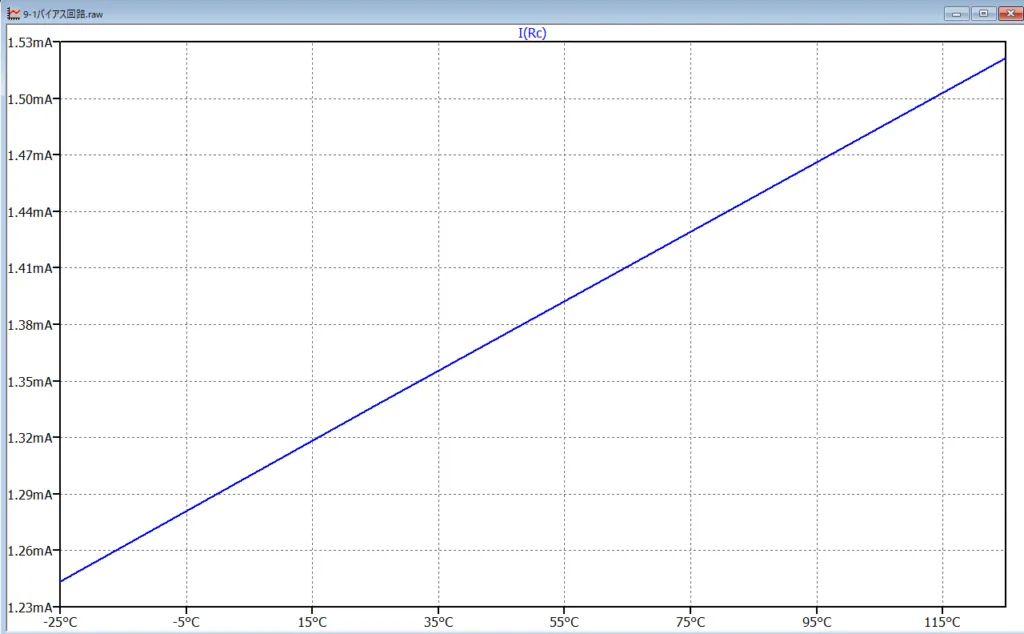
電流帰還バイアス回路の利点である温度安定性を評価するために、.op 解析に加えて .step コマンドを使って温度を変化させてシミュレーションを行う。メニューバーの.opをクリックすると図3の画面が出るので、例えば、「.step temp -25 125 50(温度 (T) を -25℃から125℃まで50℃ステップで変化させながら動作点解析を繰り返す。)」を入力し、回路図画面に貼り付ければよい。図4がシミュレーション結果で、温度変化の\(I(Rc)\)への影響を示している。
\(h_{FE}\)ばらつきのシミュレーション(安定性の評価)
\(h_{FE}\)の変動に対する安定性を評価するためには、トランジスタモデルのパラメーターを変更し、複数のシミュレーションを行う必要がある。
ディレクティブの例として、トランジスタのモデルを定義し、\(h_{FE}\)を表すパラメータ Bf を変動させる場合を以下に示す。.model Q_model NPN(Bf={beta_val}).model Q_model NPN(Bf=200).step param beta_val list 100 200 300
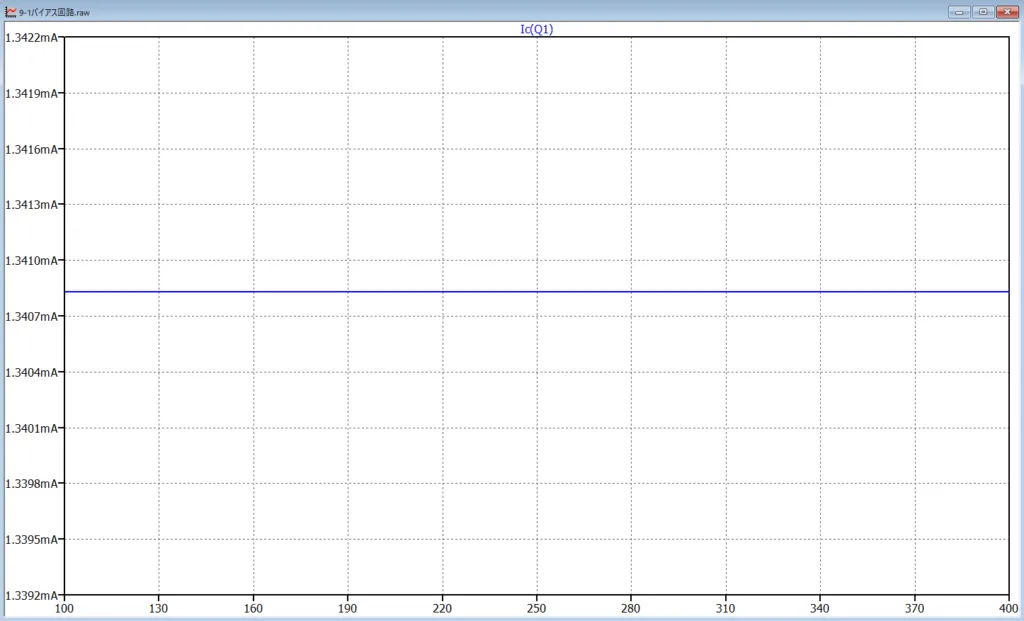
図5がシミュレーション結果で\(h_{FE}\) が変動してもトランジスタ\(Q1\)のコレクタ電流\(I_C\)がほとんど変わらないことが確認できる。
バイアスによる増幅波形への影響
.tranコマンド(過渡解析)を使って増幅波形を観測し、バイアス(Q点)の影響をみる。
入力信号\(V(vin)\)は、振幅\(1.3\;V\)、周波数\(1 \; kHz\)の正弦波とする。
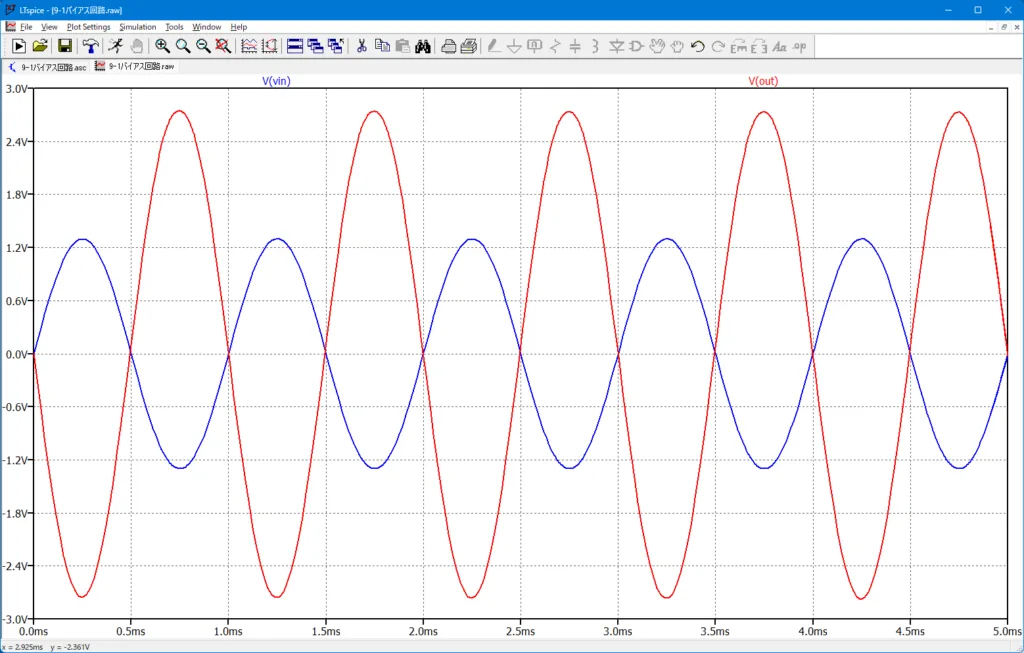
図6は適正バイアス(\(V(vb)=2.0\;V\)のときの入出力波形(\(V(vin)\):青線、\(V(out)\):赤線)である。歪もなく増幅されていることが分かる。
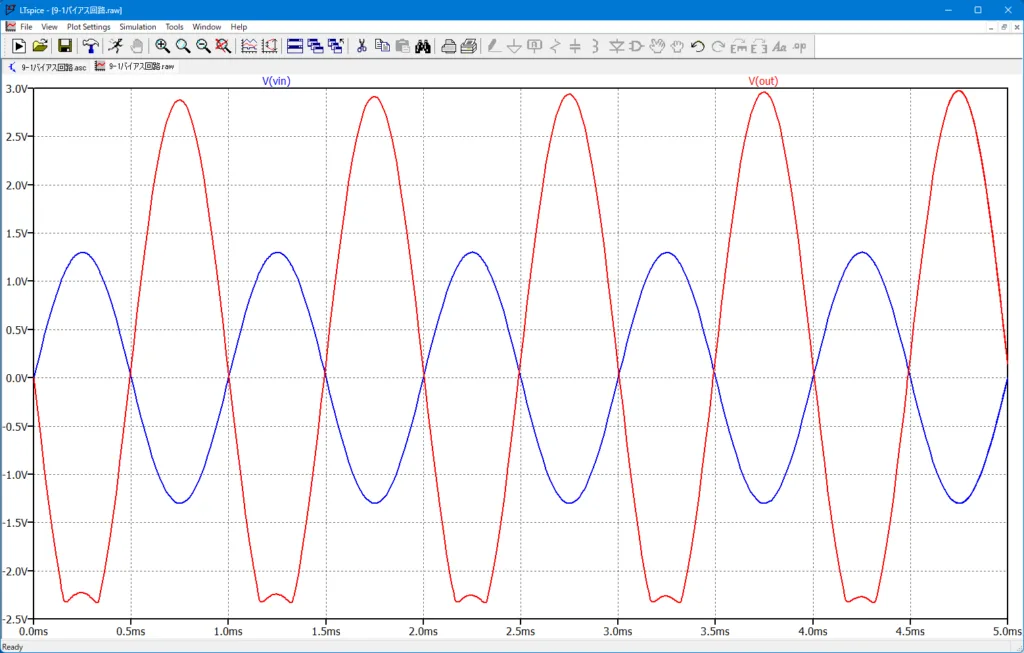
図7は、\(R2 = 15\;k\Omega\)に変え、\(V(vb) = 2.6 \; V\)とベース電圧を変えたときの入出力波形である。増幅された出力波形(\(V(out)\):赤線)が大きく歪んでいることが分かる。