31. 位相遅れ補償器

位相遅れ補償器は、特定周波数帯域の位相を遅らせる補償器である。位相遅れ補償器の伝達関数は、 $$C(s)=\frac{K(1 + \beta Ts)}{1 + Ts} \enspace \enspace (0 \lt \beta \lt 1)$$ $K=1$として、周波数特性を考える。 $$C(j \omega)=\frac{(1 + \beta T j\omega)}{1 + T j\omega}$$ 利得は、 $$|C(j\omega)|=\frac{\sqrt{1 +(\beta T\omega)^2}}{\sqrt{1 + (T \omega)^2}}$$ であり、低域では、つまり$\omega$が十分に低い領域では、$|C(j\omega)|=1$（$0$dB）となる。高域、つまり$\omega$が十分に高い領域では、$|C(j\omega)|=\beta$となり、$0 \lt \beta \lt 1$なので、利得は$0$dBより低下することになる。従って、全体の利得を上げた場合、高域の利得が低い状態で、低域の利得を上げることができる。
また、位相は、 $$\phi(\omega)=\tan^{-1}\frac{\beta T \omega}{1} - \tan^{-1}\frac{T \omega}{1}$$ $$= \tan^{-1} \beta T \omega - \tan^{-1} T \omega$$ となる。この$\phi (\omega )$が極小値をとる角周波数を求める。 $$\frac{d \phi(\omega)}{d \omega}=\frac{\beta T}{1 + (\beta T \omega)^2} - \frac{T}{1 + (T \omega)^2} = 0$$ よって、$\phi (\omega)$が極小値をとる角周波数、すなわち位相が最大に遅れる角周波数$\omega_m$は、 $$\omega_m = \frac{1}{\sqrt{\beta}T}$$ となる。この時の周波数伝達関数は、 $$C(j \omega_m)=\frac{(1 + \beta T j\omega_m)}{1 + T j\omega_m} = \frac{1 + \sqrt{\beta}j}{1 + \frac{1}{\sqrt{\beta}}j}$$ $$= \frac{2 + j(\sqrt{\beta} - \frac{1}{\sqrt{\beta}})}{1 + \frac{1}{\beta}}$$ である。よって、最大位相遅れ$\phi_m$は、 $$\phi_m = \tan^{-1}\frac{(\sqrt{\beta} - \frac{1}{\sqrt{\beta}})}{2}$$ $$= \sin^{-1}\frac{\beta -1}{\beta + 1} \enspace \enspace (0 \lt \beta \lt 1)$$ となる。
位相遅れ補償器の働きは。
・高周波域でゲインを一定値下げて安定化をはかる
・同一の定常偏差に対し安定度を向上する
・高周波域が遮断され、ノイズに対して有利になるが、速応性は劣化する
である。

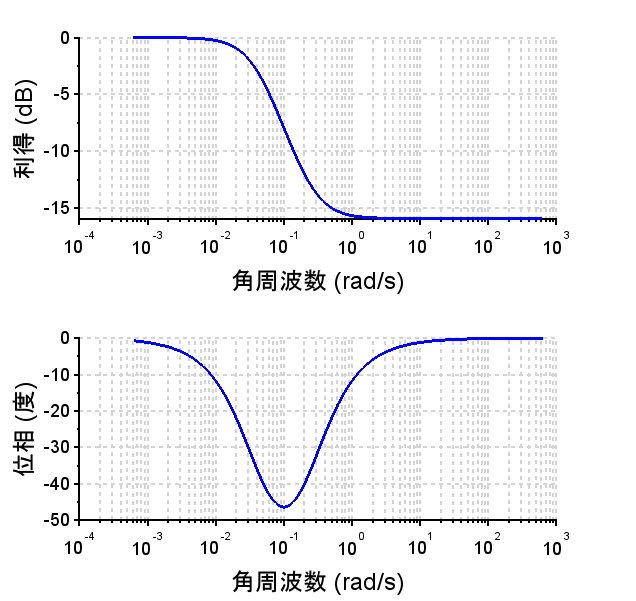
位相遅れ補償器の例
（Scilabスクリプト）

$\beta=0.16$ , $T=25$[s]とすると、
$\omega_m=0.1$[rad/s]、$\phi_m \approx -48^{°}$　となる。
図のような周波数特性で、$\omega_m=0.1$[rad/s]で最大位相遅れとなる。また、高域の利得が小さくなる（$\beta=0.16$倍$\approx -16$dB)となる。

//位相遅れ補償器
clear; clf();
s=%s;
//β=0.16，T=25
b=0.16;
T=25;
C=(1+b*T*s)/(1+T*s);
Cs=syslin('c',C);
scf(0);
bode(Cs,10^-4,10^2,'rad');