30. 位相進み補償器

位相進み補償器は、特定周波数帯域の位相を進める補償器である。位相進み補償器の伝達関数は、$$C(s)=\frac{K(1 + \alpha Ts)}{1 + Ts} \enspace \enspace (\alpha \gt 1)$$ \(K=1\)として、周波数特性を考える。$$C(j \omega)=\frac{(1 + \alpha T j\omega)}{1 + T j\omega} $$ 利得は、$$|C(j\omega)|=\frac{\sqrt{1 +(\alpha T\omega)^2}}{\sqrt{1 + (T \omega)^2}}$$であり、高域、つまり\(\omega\)が十分に高い領域では、\( |C(j\omega)|=\alpha\)となる。また、位相は、$$\phi(\omega)=\tan^{-1}\frac{\alpha T \omega}{1} - \tan^{-1}\frac{T \omega}{1} $$ $$= \tan^{-1} \alpha T \omega - \tan^{-1} T \omega$$となる。この\( \phi (\omega )\)が極大値をとる角周波数を求める。$$\frac{d \phi(\omega)}{d \omega}=\frac{\alpha T}{1 + (\alpha T \omega)^2} - \frac{T}{1 + (T \omega)^2} = 0$$ よって、\( \phi (\omega)\)が極大値をとる角周波数、すなわち位相が最大に進む角周波数\(\omega_m\)は、$$\omega_m = \frac{1}{\sqrt{\alpha}T}$$となる。この時の周波数伝達関数は、$$C(j \omega_m)=\frac{(1 + \alpha T j\omega_m)}{1 + T j\omega_m} = \frac{1 + \sqrt{\alpha}j}{1 + \frac{1}{\sqrt{\alpha}}j}$$ $$= \frac{2 + j(\sqrt{\alpha} - \frac{1}{\sqrt{\alpha}})}{1 + \frac{1}{\alpha}}$$である。よって、最大位相進み\(\phi_m\)は、$$\phi_m = \tan^{-1}\frac{(\sqrt{\alpha} - \frac{1}{\sqrt{\alpha}})}{2} = \sin^{-1}\frac{\alpha -1}{\alpha + 1} \enspace \enspace (\alpha \gt 1)$$となる。
位相進み補償器の働きは、
・高周波域（ゲイン交差周波数近傍）における一巡伝達関数の位相を進めることにより安定度を改善
・制御帯域の広帯域化による速応性の改善
である。

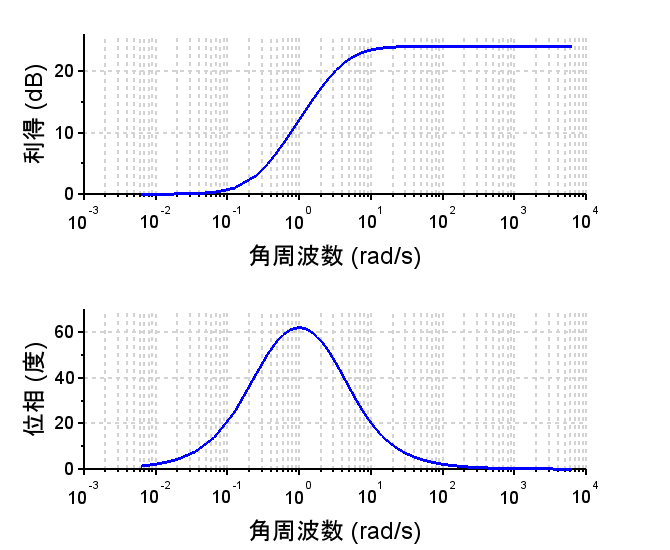
位相進み補償器の例
（Scilabスクリプト）

\(\alpha=16\) , \(T=0.25\)[s]とすると、
\(\omega_m=1\)[rad/s]、\(\phi_m \approx 62^{°}\)　となる。
図のような周波数特性で、\(\omega_m=1\)[rad/s]で最大位相進みとなる。高域の利得が大きくなる（\(\alpha=16\)倍\( \approx 24\)dB)となることに注意する必要がある。

//位相進み補償器
clear; clf();
s=%s;
//α=16，T=0.25
a=16; T=0.25;
C=(1+a*T*s)/(1+T*s);
Cs=syslin('c',C);
scf(0);
bode(Cs,'rad');

位相進み補償器による特性改善

制御対象を$$P(s)=\frac{1}{s(s+1)(s+3)}$$とする。\(P(s)\)の極は、\([0, -1, -3]\)なので安定限界（不安定）である。また、\(\frac{1}{s}\)を持っているので１型系である。
制御仕様は以下とする。
・位相余裕\(p_m=45^{°}\)程度、ゲイン余裕\(g_m=12dB\)程度、ゲイン交差周波数\(\omega_c\)はできるだけ高くとる。
・定常位置偏差\(e_p=０\)、定常速度偏差\(e_v=0.5\)を目標とする。

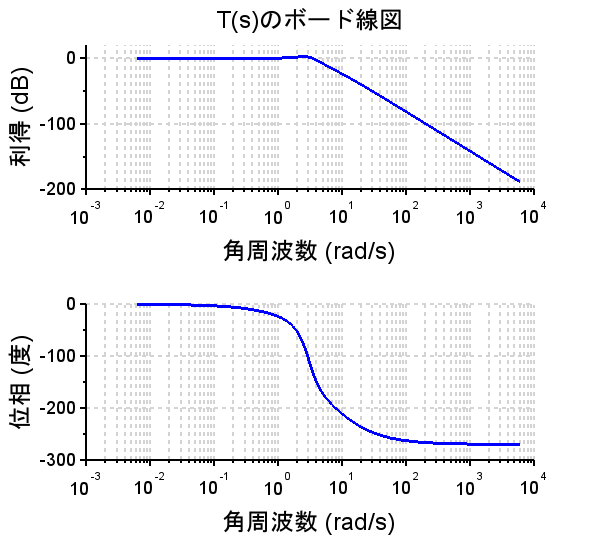
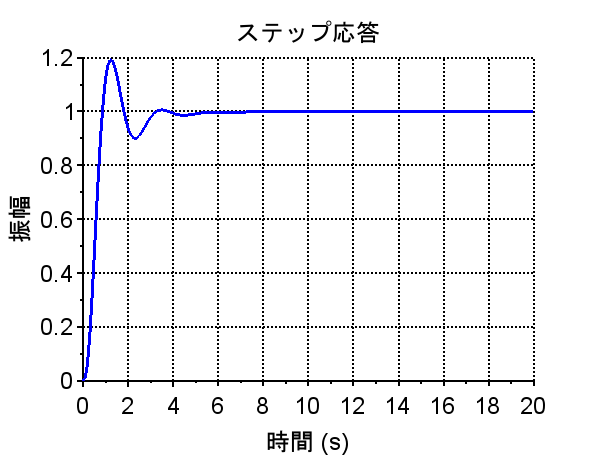
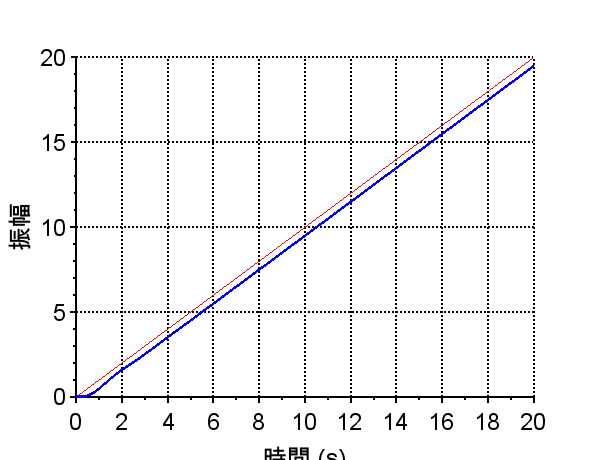
ボード線図、ステップ応答、ランプ応答より、位相余裕\(p_m \approx 46^{°}\)、ゲイン余裕\(g_m \approx 13dB\)で、制御仕様を満たしており十分な安定余裕をもっていることがわかる。ステップ応答も立ち上がり時間が短く、行き過ぎ量も小さい。しかし、ランプ応答より、定常速度偏差は制御仕様を十分に満たしているとは言えない。

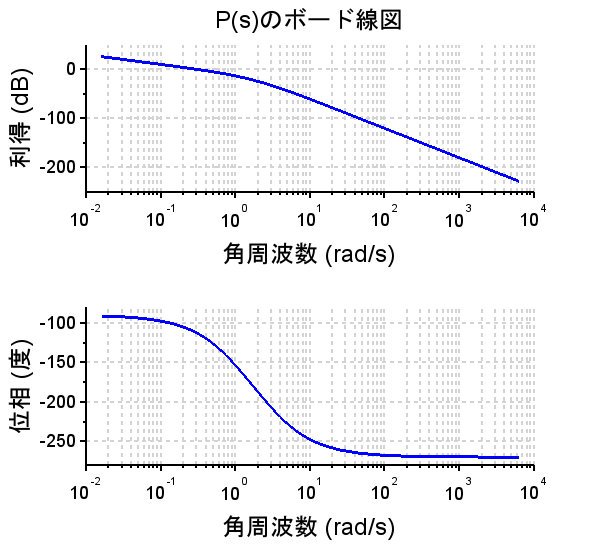
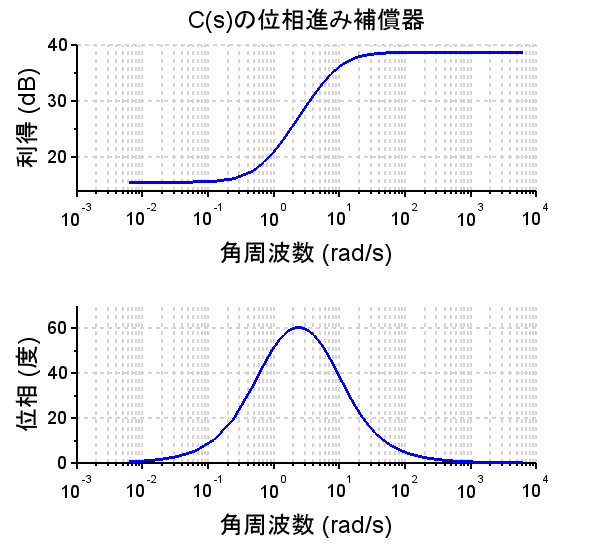
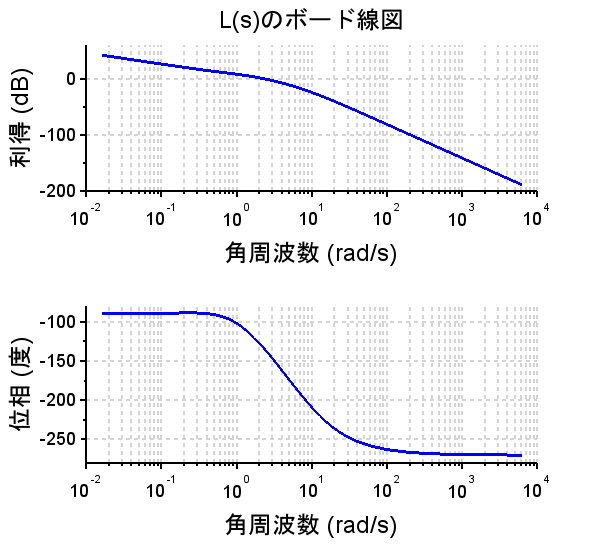
Scilabスクリプト

//位相進み補償器による特性改善
clear; clf();
s=%s;
//制御対象
P=1/(s*(s+1)*(s+3));
Ps=syslin('c',P);
scf(0);
bode(Ps,'rad');
//位相進み補償器
C=(6*(1+1.58*s))/(1+0.11*s);
Cs=syslin('c',C);
scf(1);
bode(Cs,'rad');
//開ループ伝達関数
L=C*P;
Ls=syslin('c',L);
scf(2);
bode(Ls,'rad');
pm=p_margin(Ls); /*位相余裕*/
gm=g_margin(Ls); /*利得余裕*/
//閉ループ伝達関数
T=L/(1+L);
Ts=syslin('c',T);
scf(3);
bode(Ts,'rad');
t=0:0.1:20;
scf(4);
//ステップ応答
y=csim('step',t,Ts);
plot2d(t,y,2);xgrid;
scf(5);
//ランプ応答
y=csim(t,t,Ts);
plot2d(t,t,5);
plot2d(t,y,2);xgrid;