23. 交流回路におけるインダクタの作用

交流回路において、インダクタ\(L\)（コイル）は電流の時間変化を妨げる作用を持つ素子である。インダクタは、直流回路では電流が一定であるため作用しない。交流回路では電流が周期的に変化するため、インダクタによる影響が現れる。
インダクタの働きでは、交流電流がインダクタに流れるとインダクタの中に磁界が発生する。この磁界は、インダクタに流れる電流の大きさや方向に比例し、磁束として表される。磁束は、インダクタの中に保存され、磁束が変化すると、その変化に応じて、インダクタに電圧が誘起される。つまり、インダクタは、交流電流を流すことで、電流の変化に対して磁界を発生させ、それによって電圧を誘起する。このとき、インダクタに流れる電流とその電圧降下（インダクタの両端の電圧）は\(\frac{\pi}{2}\)位相が異なる。電流に対して電圧は\(\frac{\pi}{2}\)位相が進む。
この働きを利用して、インダクタは、フィルタ回路や共振回路などに広く利用されている。

図「インダクタ\(L\)だけの回路」のように、交流起電力\(e\; [V]\)の電源とインダクタンス\(L\;[H]\)のインダクタを接続した回路に、電流\(i = I_m \sin \omega t \; [A] \; \cdots \cdots (1)\)が流れている。この電流\(i\)は時間的に変化するので、インダクタ\(L\)には、$$e_L = -L\frac{di}{dt} \;[V]$$の自己誘導起電力が発生する。

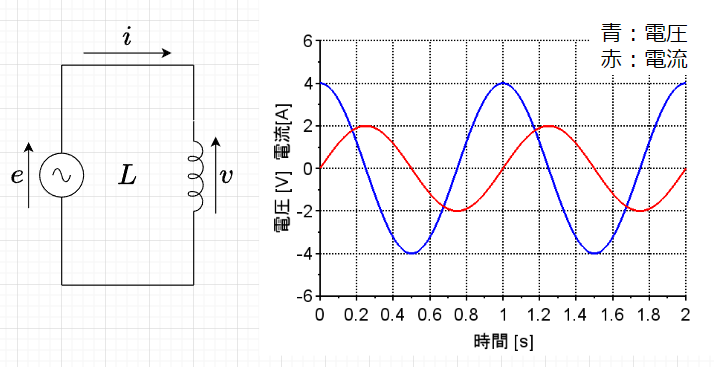
自己誘導作用で生じる起電力は電流の増減を妨げる方向に生じるため、自己誘導起電力\(e_L\)には負の符号がつく。$$e_L = -L\frac{di}{dt} =-LI_m\frac{d \sin \omega t}{dt}=-LI_m\omega \cos \omega t = \omega LI_m \sin \left(\omega t - \frac{\pi}{2} \right) \; [V]$$インダクタのなかに生じる起電力は供給電力に逆らう作用をなすので、逆起電力と呼ばれる。この逆起電力に逆らって回路に電流を流すために、供給電圧（交流起電力）\(e\)と逆起電力\(e_L\)との関係は、$$e + e_L = 0$$となる、よって、$$e = -e_L = - \omega LI_m \sin \left(\omega t - \frac{\pi}{2} \right) = \omega LI_m \sin \left(\omega t + \frac{\pi}{2} \right) \;[V] \; \cdots \cdots (2)$$となる。すなわち、供給電圧は、最大値（振幅）が\(\omega L I_m\)で、位相が電流よりも\(\pi/2\)進んだ電圧となる。図「インダクタ\(L\)だけの回路」の右図の波形のようになる。

インダクタに加える電圧の実効値、電流の実効値をそれぞれ\(E \; [V] ,\;\;\; I\;[A]\)とすると、電圧と電流の大きさの関係は、$$E= \omega L I \;[V] \\ I = \frac{E}{\omega L} \; [A]$$となる。ここで、\( \omega L \; [\Omega] \)は誘導性リアクタンスと呼ばれ、抵抗のように電流を制限する働きがある。単位は\(\Omega\)である。

この誘導性リアクタンスは、記号\(X_L\)で表され、$$X_L = \omega L = 2 \pi f L \; [\Omega]$$である。誘導性リアクタンスの大きさは角周波数（周波数）\(\omega =2\pi f\)に依存するので、周波数が高いほど、つまり、電流の変化が大きいほど電流の流れを妨げる\(X_L\)は大きくなる。逆に電流の変化が無いとき、すなわち、直流では\(X_L=0\; [\Omega]\)となる。
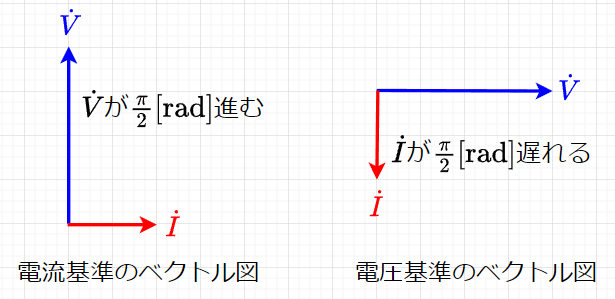
電圧と電流の関係をベクトル図で表すと、図「インダクタ\(L\)だけの回路のベクトル図」のように電圧\(\dot{V}\)、電流\(\dot{I}\)のベクトル図として表せる。
\(V,I\)をベクトル図で示すときは、角周波数がともに\(\omega \; [\mathrm{rad}/s]\)で一定であるから、これらの相対関係は時間\(t\)に無関係となるので、\(t=0\)の状態で表示する。従って、\( \dot{V}, \;\dot{I} \)の位相は、\(t=0\)における初期位相で示すことになる。
図「インダクタ\(L\)だけの回路のベクトル図」では、式\((1),(2)\)で\(\dot{I}, \; \dot{V} \)の初期位相がそれぞれ\(0[\mathrm{rad}], \;\; \pi /2 [\mathrm{rad}]\)であるから、図「インダクタ\(L\)だけの回路のベクトル図」の「電流基準のベクトル図」のようになる。また、電圧\(\dot{V}\)を基準に描くと「電圧基準のベクトル図」のようになる。
一般にベクトル図を描く場合、直列回路では各素子に共通要素の電流\(I\)を、並列回路では各素子に共通な要素の電圧\(V\)を基準にして描くことが多い。