31. 疑似微分器の実装

※注意：理論の検証的な話題で、実用性はあまりないと思われる。

疑似微分器（Practical Differentiator）は、理想的な微分器が抱える「ノイズへの弱さ」や「動作の不安定さ」を克服するために、あえて高域のゲインを制限した回路のことである。電気電子回路での理想的な微分器の伝達関数は\(G(s) = s RC\)、周波数伝達関数\(G(j \omega)= j\omega RC\)（角周波数\(\frac{1}{RC}\)において利得が0 dB)で表される。これは周波数が高くなればなるほどゲインが無限に大きくなる特性を持つ。このため、高域ノイズの増幅（高周波の微小なノイズ（熱雑音など）を過大に増幅し、信号が埋もれてしまう）、回路の不安定化（オペアンプの位相遅れと組み合わさり、発振しやすくなる）という問題点を持つ。これらを解決するため、高域でゲインを抑える（ローパスフィルタの特性を持たせる）のが疑似微分器で、伝達関数は一般的に式(1)のような形になる。$$G(s) = \frac{s}{s + \omega_c}, \; \quad \omega_c = \frac{1}{CR}: 遮断角周波数\quad \cdots (1)$$式(1)は、式(2)のように変形できる。$$G(s) = \frac{s}{s + \omega_c} \\= 1 - \frac{\omega_c}{s + \omega_c} \; \quad \cdots (2)$$式(2)の第２項\(\frac{\omega_c}{s + \omega_c}\)はLPFとなっている。つまり、全域通過（入力信号そのもの）からLPFの出力を減算することで、疑似微分器（1次HPF）が実装できることを示している。
オペアンプ回路で「微分」を直接行うのではなく、「入力から積分成分（低域成分）を引く」という形で疑似微分器を作ることになる。この利点は以下となる。
・高域ノイズに対する安定性：理想的な微分器は入力にコンデンサを直列に配置するが、これは高周波ノイズを過大に増幅し、オペアンプの出力を飽和（クリップ）させたり、回路を発振させたりする原因になる。
一方、\(\frac{\omega_c}{s+\omega_c}\)の部分はLPF（積分器に相当）である。積分器はノイズを滑らかにする性質があるため、演算過程でノイズを増幅しにくく、回路全体の動作を安定にする。
・入力インピーダンスの確保と突入電流の防止：コンデンサを入力に直列に入れる微分器は、高周波において入力インピーダンスが極めて低くなり、前段の回路に大きな負荷をかける。積分器ベースの構成（加減算器とローパスフィルタの組み合わせ）にすると、入力インピーダンスを抵抗で制御しやすくなり、急峻な信号変化時の突入電流（スパイク）を抑制する。
・実装の容易さと精度の向上：オペアンプにおいて、微分器（進み要素）を作るよりも、積分器（遅れ要素）を作るほうが簡単で精度が出やすい。積分器は位相が遅れる方向（安定方向）に働くため、帰還ループを組みやすく、設計値通りの遮断周波数を実現しやすい。

回路構成例とシミュレーション

図１はオペアンプで実装した疑似微分器（１次HPF）の回路例である。図２は周波数特性で、低域（遮断周波数：約160 Hz)以下では微分特性を示し、高域の利得は0 dBとなっている。位相特性は、低域で90度進んでいる。

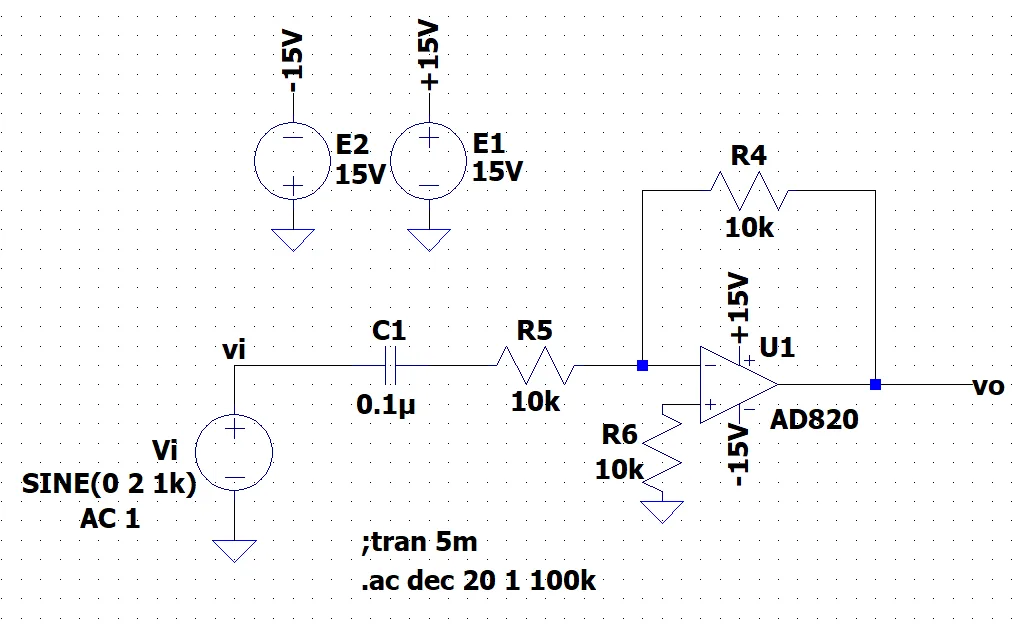
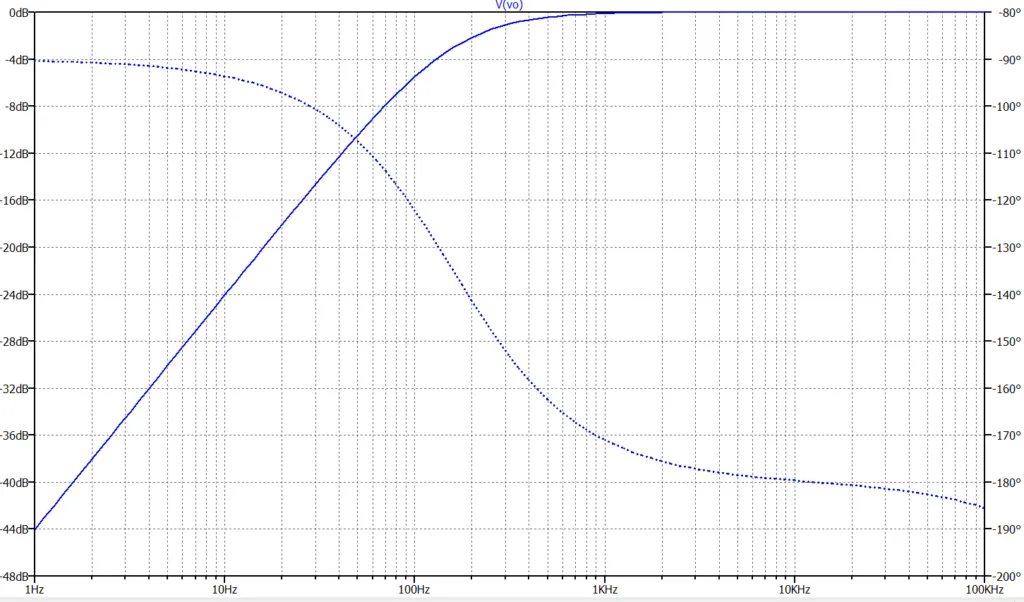
図３に疑似微分器をLPFで実装する回路例を示す。図４は周波数特性で、図２と同様な特性となっている。

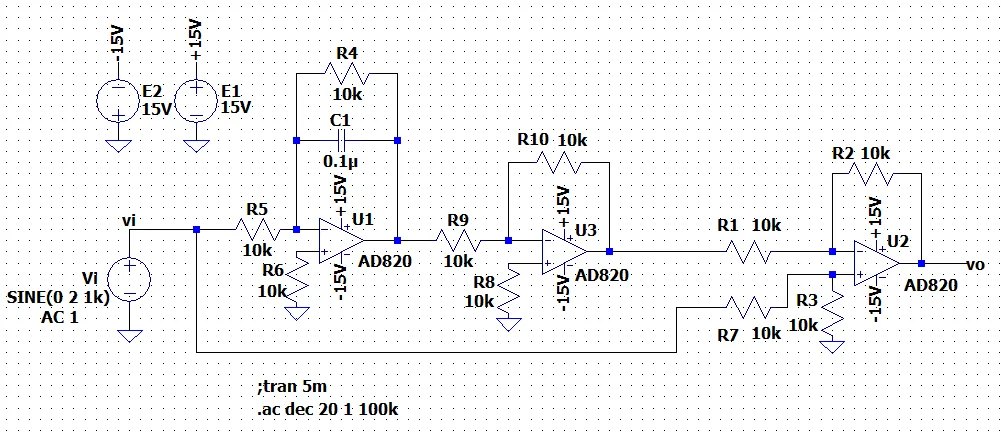
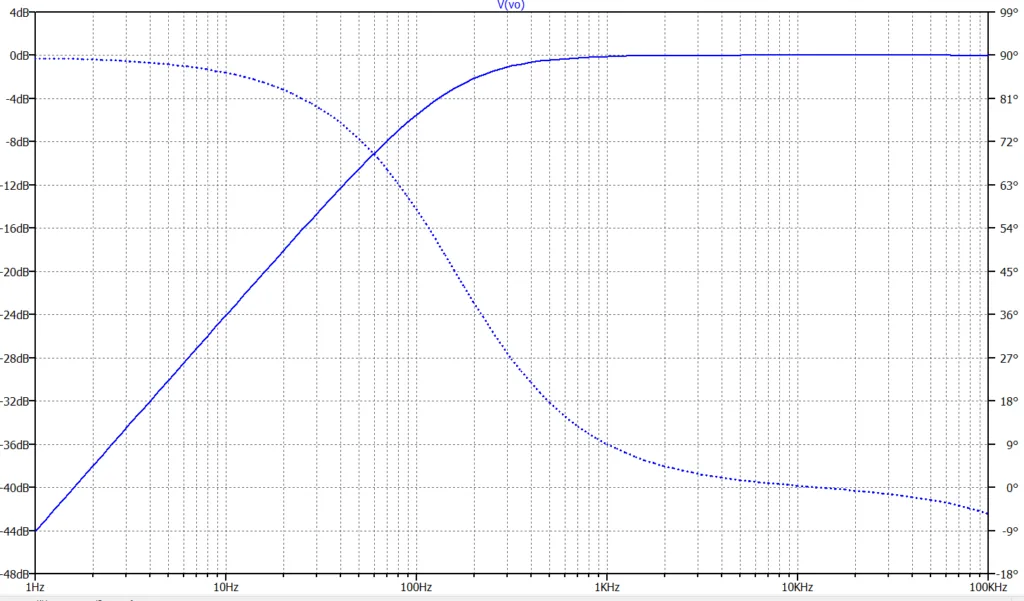
図１の構成は、部品点数が少なく一次HPFとして一般的によく使われる回路構成である。図３の構成は、部品点数が多くなるが、以下の利点がある。
・パラメータの独立性：微分として機能させたい帯域（\(\omega_c\)）を、LPFの時定数だけで独立して決定できる。
・飽和に強い：信号を一度滑らかなLPFに通すため、急激な変化（スパイクノイズ）が直接オペアンプの入力に入って出力が振り切れるリスクが減る。
・制御理論との親和性：PID制御などを組む際、内部で「現在の値」と「平均的な値（LPFを通したもの）」の差を取ることで微分成分を得る手法は、デジタル信号処理（DSP）でもよく使われる非常に安定した手法である。
一方、図３の構成は、回路が複雑になるだけでなく、各回路（オペアンプ）の精度が高くないと、オフセット電圧の累積、同相信号除去比の問題などがあり実用的には難しい面がある。
まとめると、一般的なセンサー信号の微分であれば、部品が少なく安定している「1つのオペアンプによる疑似微分器（実用的微分回路）」が推奨され、一方で、「低域の特性を精密に管理したい」場合や、「デジタル信号処理（DSP）のアルゴリズムをそのままアナログでシミュレートしたい」という特殊な場合には、減算器＋LPFの構成が検討に値する。