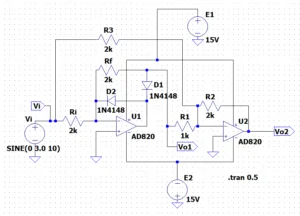
11-1. BJTのモデル
BJT(バイポーラトランジスタ)を使った回路の解析には、LTspiceなどの電子回路シミュレーションツールが欠かせない。LTspiceは、SPICE (Simulation Program with Integrated Circuit Emphasis) という回路シミュレーションの基盤技術をベースに、Analog Devices社が無償で提供している高性能な電子回路シミュレータである。SPICEは汎用的なシミュレーションの「エンジン」であり、LTspiceはそのエンジンにグラフィカルインターフェース(回路図エディタ、波形ビューア)と、自社製品の部品モデルを組み込んだアプリケーションである。 SPICEで用いられるBJTのモデルは、主にEbers-MollモデルとGummel-Poonモデルの二つが基本となる。
BJTの物理構造と寄生素子
BJTにはNPN形とPNP形があるが、ここではNPN形で考える。NPN形トランジスタの一般的な構造は、図1のようにP形基板にコレクタ領域となるN形層が形成され、その中にP形のベース領域、さらに\(\text{N}^+\)形(不純物のドーピング濃度の高いN形)のエミッタ領域を形成する。電流の流れを改善するために抵抗の小さい\(\text{N}^+\)埋め込み層等を組み込む。図中において点線で囲まれた部分は、真性トランジスタ領域と呼ばれ、2つの理想的なPN接合構造(ダイオード)が形成されている。この構造によってBJTは、エミッタ(E)からベース(B)に注入された少数キャリア(NPN形なので電子)が、コレクタ(C)へ到達したときに流れるコレクタ電流を数桁小さいベース電流によって制御できる電流制御型電流素子となっている。以上の説明は、B-E間(ベース・エミッタ間)を順バイアス、B-C間(ベース・コレクタ間)を逆バイアスとしてトランジスタを使用した場合の順動作特性についてのものである。
BJTは、構造上多くのPN接合(ダイオード)を含んでいるため各種容量や抵抗を有し、これらを総称して寄生素子と呼ぶ。図1にはこれらの寄生素子も含めて、BJTを構成している各種素子を電気記号によって記入している。
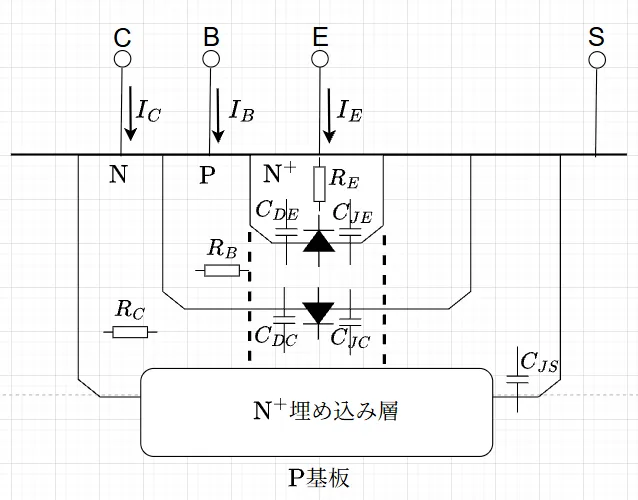
図1の各記号は、以下である。
N:N形半導体、P:P形半導体、\(\text{N}^+\):ドーピング濃度の高いN形半導体
C:コレクタ、B:ベース、E:エミッタ、S:基板
\(I_C\):コレクタ電流、\(I_B\):ベース電流、\(I_E\):エミッタ電流
\(R_E,\; R_B,\; R_C\):寄生抵抗
\(C_{DE},\; C_{DC}\):拡散容量
\(C_{JE},;C_{JC},\;C_{JS}\):接合容量
Ebers-Moll モデル(簡略モデル)
Ebers-Mollモデルは、BJTの基本的な直流(DC)動作を記述するための、最もシンプルな初期モデルである。基本的にトランジスタを2つのダイオードと2つの電流源の組み合わせで表現する。能動領域・飽和領域・逆動作領域を一つの式体系で連続的に表現できるのが特徴である。
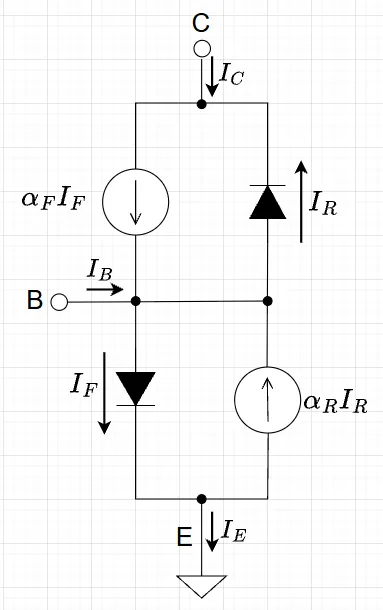
図2にEbers-Mollモデルの概念図を示す。ベース電流\(I_B\)は、ベース・エミッタ間とベース・コレクタ間に流れるダイオード電流\(I_F,\;I_R\)の和で表される。コレクタ電流\(I_C\)には、\(I_R\)の他にエミッタからベースに注入されコレクタに流れる少数キャリアによる拡散電流\(\alpha_F I_F\)が加わり,エミッタ電流\(I_E\)には同様に\(I_F\)に\(\alpha_R I_R\)が加わる。ここで、\(\alpha_F,\; \alpha_R\)は、ベースに注入された少数キャリアがベース領域を通り抜けてコレクタ、エミッタまで到達する比率を表す。\(\alpha_F\approx 0.98~0.998, \quad \alpha_R << \alpha_F\)
1)BE 接合ダイオード(ベース–エミッタ間の pn 接合)電流は、$$I_F = I_{ES} \left(e^{\frac{V_{BE}}{V_T}}−1\right)。$$
2)BC接合ダイオード(ベース–コレクタ間の pn 接合)電流は、$$I_R = I_{CS} \left(e^{\frac{V_{BC}}{V_T}}−1\right)。$$
\(I_{ES},\; I_{CS}\)は,それぞれのダイオードの飽和電流である。\(V_T\)は熱電圧で、$$V_T = \frac{kT}{q}$$で表される。\(k\):ボルツマン定数、\(T\):絶対温度[K]、\(q\):電子の電荷量で、\(V_T \approx 25.8 \;[\text{mV}]\)(300 K:室温 約27℃)である。
端子電流の基本式(NPN)は、$$I_C = \alpha_F I_{ES} \left(e^{\frac{V_{BE}}{V_T}}-1\right) - I_{CS}\left(e^{\frac{V_{BC}}{V_T}}-1\right) \\ I_E = I_{ES} \left(e^{\frac{V_{BE}}{V_T}}-1\right) - \alpha_R I_{CS}\left(e^{\frac{V_{BC}}{V_T}}-1\right) \\ I_B = I_E -I_C$$となる。
Gummel-Poon モデル(高精度モデル)
Gummel-Poonモデルは、Ebers-Mollモデルを拡張し、特にベース幅変調(アーリー効果)や高注入効果(ハイインジェクション効果)など、多くの非線形効果を組み込んだ高精度のモデルである。現代の回路シミュレーションでは、ほぼこのモデルが使用されている。特徴として以下が挙げられる。
・高精度: 広い動作範囲(低電流から高電流まで)で正確な直流(DC)特性と交流(AC)特性をシミュレーションできる。
・ベース電荷の概念: ベースに蓄積される電荷\(Q_B\)を中心にモデルが構成されており、この電荷の変化によって電流や容量を計算するため、過渡応答(トランジスタのスイッチング動作)のシミュレーション精度が向上している。
Gummel-Poon 直流モデル
図3に示すGummle-Poon直流モデルは、トランジスタの増幅作用に最も影響を及ぼしているのはベース中の電荷であるということに注目して、トランジスタの特性がベース電荷密度で決定されるという概念を用いることによって提案されたものである。低注入状態での電流増幅率の低下を取り入れるため、ベース電流に加わる再結合電流および洩れ電流を表す非理想ダイオードをエーバスモルモデルの理想電流を表すダイオードに並列に追加することによって精度を向上させている。
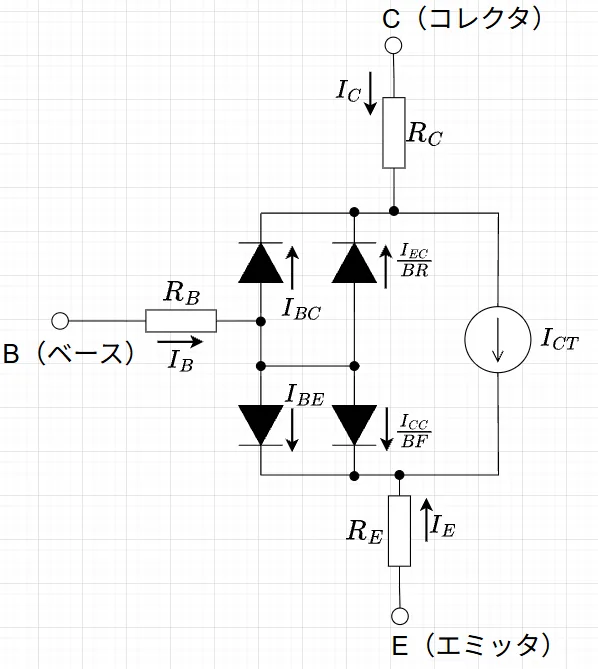
この非理想ダイオード電流\(I_{BE}, \; I_{BC}\)は、$$I_{BE} = I_{SE}\left(e^{\frac{V_{BE}}{NE \cdot V_T}}-1\right) ,\quad I_{BC} = I_{SC}\left(e^{\frac{V_{BC}}{NC \cdot V_T}}-1\right)$$である。ここで,\(I_{SE},\; I_{SC}\)は、それぞれB-E間、B-C間の洩れ飽和電流、また、\(NE,\;NC\)は、各接合における洩れ放射係数である。
また、理想ダイオード電流\(I_{CC}, \; I_{EC}\)は、$$I_{CC} = \frac{I_S}{q_b}\left(e^{\frac{V_{BE}}{NF \cdot V_T}}-1\right) , \quad I_{EC} = \frac{I_S}{q_b}\left(e^{\frac{V_{BC}}{NR \cdot V_T}}-1\right)$$で表す。ここで、 \(q_b\)はベース領域の電荷密度で、熱平衡状態でのベース電荷密度で規格化されたベース電荷密度\(q_b\)によって表される。高注入状態では、電流によってベース領域の少数キャリア数がそこでの多数キャリア数と同等もしくはそれ以上に増加するため、電荷中性を保つように多数キャリアも増加する。この多数キャリアの増加は、ベース領域の不純物濃度を増加させたことに等価であるため注入効率が低下し、その結果、コレクタ電流が減少する。つまり、電流利得の低下を、ベースに蓄積される実効的な電荷 \(q_b\)の増加に起因するものと考えている(高注入効果)。実際のベース領域の電荷密度は、熱平衡状態でのベース電荷密度で規格化されたベース電荷密度\(q_b\)によって表現されており、以下の式となっている。$$q_b = 1+q_e+q_c+q_{bF}+q_{bR}$$ \(q_e\)と\(q_c\)はアーリー効果、\(q_{bF}\)と\(q_{bR}\)が高注入効果を表している項である。
Gummel-Poon 大信号モデル
Gummel-Poon大信号モデルを図4に示す。直流モデルにバイポーラトランジスタの構造等によって生じる各種の寄生容量を陽に表現したモデルである。このモデルは、回路の過渡解析に適している。接合容量\(C_{JC},\;C_{JE},\;C_{JS}\)は,トランジスタ中の各PN接合(ダイオード)にかかる電圧\(V_D\)と拡散電位差\(V_J\)の大小関係によって2つに分けられ、以下に示すダイオードモデルで説明された接合容量式で表される。
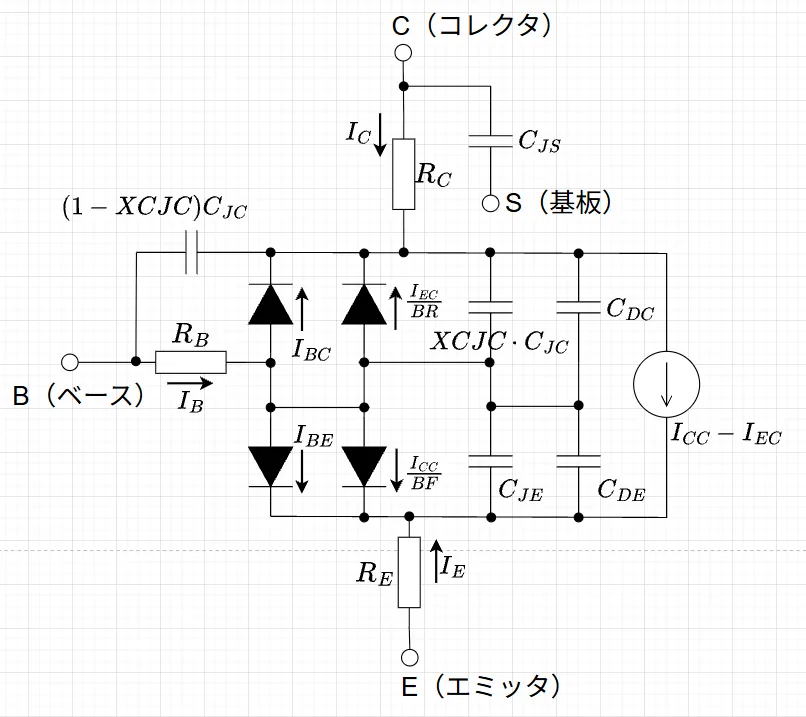
・\(V_D \leq V_{J}\)の場合:$$C_{JC} = \frac{C_{J0}}{(1-V_D/V_{J})^{MJC}}, \quad C_{JE} = \frac{C_{J0}}{(1-V_D/V_{J})^{MJE}}, \quad C_{JS} = \frac{C_{J0}}{(1-V_D/V_{J})^{MJS}}$$・\(V_D > V_J\)の場合:$$C_{JC} = \frac{C_{J0}}{(1 - FC)^{MJC}}\left\{1 + \frac{MJC(V_D - FC \cdot V_J)}{V_J(1 - FC)}\right\} \\ C_{JE} = \frac{C_{J0}}{(1 - FC)^{MJE}}\left\{1 + \frac{MJE(V_D - FC \cdot V_J)}{V_J(1 - FC)}\right\} \\ C_{JS} = \frac{C_{J0}}{(1 - FC)^{MJS}}\left\{1 + \frac{MJS(V_D - FC \cdot V_J)}{V_J(1 - FC)}\right\}$$また,B-E間、B-C間容量には上式の接合容量のほか、それぞれの間に拡散容量\(C_{DE}, \;C_{DC}\)が並列に加わる。拡散容量は接合に電流が流れたとき、ベース中性領域に蓄積される少数キャリアによる容量である。この少数キャリアによる蓄積電荷は、中性ベース領域の順動作(逆動作)キャリア走行時間とそこを流れるコレクタ電流(エミッタ電流)の積で表される。従って、拡散容量はこの蓄積電荷を各接合間電圧で微分することによって得られる。ここで、順、逆動作のキャリア走行時間(\(\tau_F,\; \tau_R\))は、高注入状態では少数キャリア数の増加とともに大きくなるので、大信号モデルでは熱平衡状態の順、逆動作のキャリア走行時間(\(TF,\;TR\))と規格化ベース電荷密度\(q_b\)との積で表される。
高注入状態を考慮した大信号モデルにおける実効的な順方向キャリア走行時間 \(\tau_F\)を表す式は以下となる。
・実効キャリア走行時間\(\tau_F\):高注入状態でのベース走行時間の増加を、規格化ベース電荷 \(q_b\) を用いて表現する。コレクタ電流\(I_C\)を、理想的な電流\(I_{CC}\)と規格化ベース電荷 \(q_b\) の比で定義する。$$I_C = \frac{I_{CC}}{q_b}$$ここで、規格化ベース電荷\(q_b\)は、ベースに蓄積された実効的な電荷であり、ベース幅変調(アーリー効果)や高注入効果といった非理想的な現象によって増加する。$$\tau_F = TF \cdot \left(1 +XTF \cdot \exp\left(\frac{V_{BC}}{VTF \cdot V_T}\right) \cdot \left(\frac{I_C}{IS} \right)^{ITF} \right)$$ただし、この式の導出の出発点となる、ベースに蓄積される総電荷\(Q_b\)の中で、高注入が関わる実効的な順方向キャリア走行時間\(\tau_F\)は、規格化ベース電荷\(q_b\)を基準の走行時間\(TF\)で補正したものである。式\(\tau_F = \ldots\)は、以下のように解釈できる。$$\left( \begin{matrix} \text{実効的な} \\ \text{走行時間} \\ \tau_F \end{matrix} \right) = \left( \begin{matrix} \text{理想的な} \\ \text{走行時間} \\ \mathbf{TF} \end{matrix} \right) \times \left[ 1 + \left( \begin{matrix} \text{ベース幅変調} \\ \text{(アーリー効果)} \\ \text{による増加率} \end{matrix} \right) + \left( \begin{matrix} \text{高注入} \\ \text{による} \\ \text{増加率} \end{matrix} \right) \right]$$このように、実効的な走行時間\(\tau_F\)は、ベース電荷\(q_b\)の増加に起因する非理想的な現象のすべてを集約し、その効果を電流\(I_C\)と電圧\(V_{BC}\)の関数として表現している。シミュレータはこの\(\tau_F\)を使って \(C_{dE}\)を計算し、過渡解析の精度を確保している。
※解釈の式で和になっているのは、SPICEのモデル式(\(\tau_F\)の式)としては、各パラメータの役割を明確にするために加算的(和)な補正項として記述されているためである。理論式のように積としないのは、計算の安定性とパラメータフィッティングのしやすからとされている。(和)の近似による誤差は、実際の回路設計で特定のケース(超高周波動作など)で問題になる。
・拡散容量\(C_d\):拡散容量は、接合に順バイアスがかかっているときに、ベース領域に蓄積される少数キャリア電荷\(q\) の変化に対応する容量である。これは主に高周波・高電流領域でのトランジスタのスイッチング速度(遅延時間)に関わる。拡散容量は、蓄積される電荷\(q\)を電圧\(V\)で微分したものとして定義する。$$C_d = \frac{dq}{dV}$$Gummel-Poonモデルでは、順方向の電荷蓄積時間\(TF\)(Transit Time)とコレクタ電流\(I_C\)を用いて、エミッタ・ベース接合の順バイアス時に以下のように表現される。$$C_{dE} = TF \cdot \frac{I_C}{V_T} \quad \text{(順方向動作時)}$$同様に、逆方向の拡散容量 \(C_{dC}\)は、逆方向ベース走行時間 \(TR\) を用いて表現されるが、通常は順方向動作時の\(C_{dE}\)が支配的である。
| パラメータ | 物理的意味 |
| \(\tau_F\) | 実効的な順方向キャリア走行時間(ベース拡散容量 \(C_{dE}\) の計算に利用される) |
| \(TF\) | 熱平衡状態(低電流)での順方向キャリア走行時間(Spiceパラメータ) |
| \(V_{BC}\) | ベース・コレクタ間電圧 |
| \(I_C\) | コレクタ電流 |
| \(IS\) | 飽和電流(基準電流)(Spiceパラメータ) |
| \(V_T\) | 熱電圧 \(kT/q\) |
| \(XTF\) | トランジット時間温度依存性係数(通常は1)(Spiceパラメータ) |
| \(VTF\) | アーリー効果による \(\tau_F\)の電圧依存性パラメータ(Spiceパラメータ) |
| \(ITF\) | 高注入効果による \(\tau_F\)の電流依存性パラメータ(\(\text{IKF}\) と関連)(Spiceパラメータ) |
Gummel-Poon 小信号モデル
Gummel-Poon 小信号モデルを図5に示す。直流および大信号モデルにおいては、B-E間、B-C間のダイオードに流れる電流、容量およびC-E間の電流源はいずれも非線形特性になっている。小信号モデルは、非線形特性を有する素子を線形化して扱い、電圧の関数として表されている電流はその電圧で微分する。つまり、大信号モデルの各電流・電荷の式を動作点(バイアス点)の電圧で微分することで導出される。特に\(G_\pi\)は、ベース電流\(I_B\)をB-E間電圧\(V_{BE}\)で微分した値として定義される。微分された結果である\(G_\pi,G_\mu,G_O\)は素子の両端の電圧の関数なのでコンダクタンスに、また、両端以外の電圧の関数である場合は電圧制御電流源\(G_m \cdot V_{BE}\)に置き換える。
これらのパラメータを配置した小信号モデルでは内部抵抗や寄生容量も動作点に依存して決定され、これら各パラメータは、SPICEシミュレータが .AC 解析(小信号交流解析)を行う際に、内部で各バイアス点ごとに計算している。
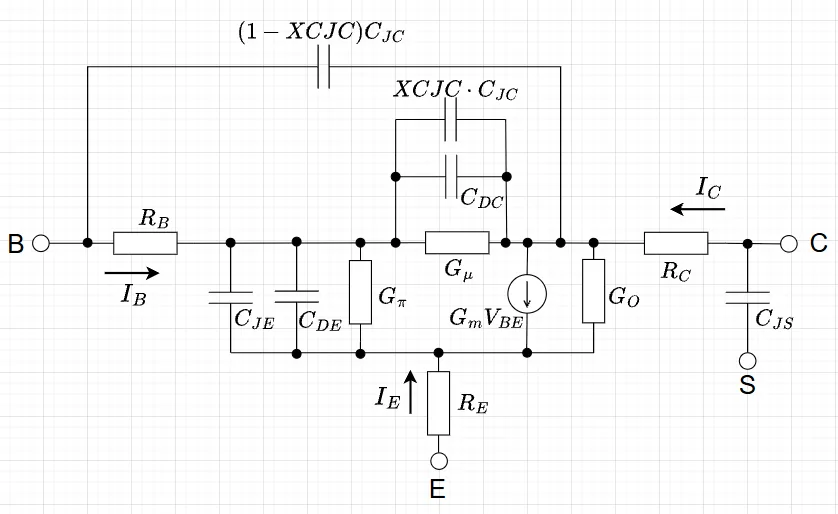
コンダクタンス\(G_m\) (伝達コンダクタンス):$$G_m = \frac{\partial I_C}{\partial V_{BE}}$$コンダクタンス \(G_\pi\) (入力コンダクタンス):$$G_\pi = \frac{\partial I_B}{\partial V_{BE}} = \frac{1}{r_\pi}$$コンダクタンス \(G_\mu\) (フィードバックコンダクタンス):$$G_\mu = \frac{\partial I_B}{\partial V_{BC}}$$コンダクタンス\(G_O\) (出力コンダクタンス):$$G_O = \frac{\partial I_C}{\partial V_{CE}}$$
Gummel–Poonモデルのモデルパラメータ
パラメータの詳細は、Gummel-Poon_modelを参照してください。
| カテゴリ | SPICE パラメータ | 物理的意味 |
|---|---|---|
| DC特性(電流利得・飽和) | ||
| 基本電流・増幅 | IS | エミッタ飽和電流(基準電流 \(I_S\)) |
| BF | 順方向最大電流利得(最大 \(\beta_F\)) | |
| NF | 順方向理想度係数 \(n_f\) | |
| BR / NR | 逆方向最大電流利得 / 理想度係数 | |
| 非線形効果と抵抗 | ||
| 高注入効果 | IKF | 高注入による \(\beta\) 低下が始まるコレクタ電流 \(I_{KF}\) |
| アーリー効果 | VA | アーリー電圧(ベース幅変調の記述)\(V_A\) |
| 内部抵抗 | RB | ベース抵抗 \(R_B\) |
| RC | コレクタ抵抗 \(R_C\) | |
| RE | エミッタ抵抗 \(R_E\) | |
| AC・過渡特性(容量と時間) | ||
| 走行時間 | TF / TR | 順方向 / 逆方向ベース走行時間(Transit Time \(\tau_F, \tau_R\)) |
| 空乏層容量(EB接合) | CJE | ゼロバイアス EB接合容量 \(C_{JE0}\) |
| MJE / VJE | EB接合のグレーディング係数 \(m_{JE}\) / ビルトイン電位 \(V_{JE}\) | |
| 空乏層容量(CB接合) | CJC | ゼロバイアス CB接合容量 \(C_{JC0}\) |
| MJC / VJC | CB接合のグレーディング係数 \(m_{JC}\) / ビルトイン電位 \(V_{JC}\) | |
| ブレークダウン特性(耐圧) | ||
| 降伏電圧 | BVCBO | コレクタ・ベース間降伏電圧 \(BV_{CBO}\) |
| BVEBO | エミッタ・ベース間降伏電圧 \(BV_{EBO}\) | |