28. 指数・対数関数(複素関数)
指数関数の像
実数の指数関数 \(f(x) = e^x\)の場合、入力(定義域)は1次元の実数直線、出力(値域)も1次元の実数直線なので、入力を横軸、出力を縦軸にとることで2次元のグラフとして描くことができる。しかし、複素指数関数\(f(z) = e^z\)の場合、入力 \(z = x + jy\) は、2次元の複素平面(\(x\)軸が実部、\(y\)軸が虚部)であり、出力\(w = f(z) = e^z = u + jv\)も、2次元の複素平面(\(u\)軸が実部、\(v\)軸が虚部)となり、合計4次元が必要となり、通常のグラフとしては描けない。
この4次元の関係性を、2次元の平面で表現するために、主に以下の二つの方法が用いられる。
1.定義域と値域を別々に描く(写像としての可視化)
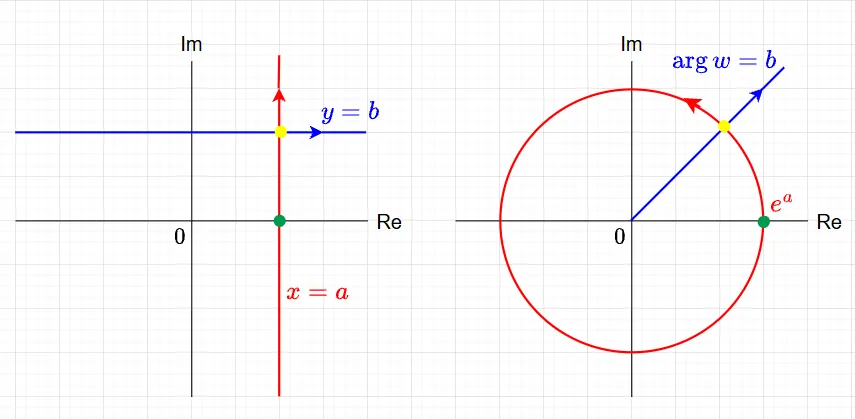
基本的な場合としてz がz-平面を垂直または水平に移動する場合を考える。以下、\(z = x + jy \quad (x; y \in R)\) とする。図1を参考に指数関数による像を考える。
*縦方向の動き:\(x=a\)を固定して、\(z=a+jy \quad (y \in \mathbb R)\)を考えると、\(w = e^z =e^{a+jy}= e^a(\cos y + j \sin y)\)となる。この場合、\(e^a > 0\)で固定され、偏角\(y\)が変化するので、\(z\)が\(x=a\)上を上方向に移動すると(図1(左)の赤線)、\(w\)は原点を中心とした半径\(e^a\)の円上を左方向に回ることになる(図1(右)の赤線)。\(z\)が上方向に\(2\pi\)動くと\(w\)は円上を一周する。また、\(a\)の値が円の半径を決めることになる。
*横方向の動き:\(y=b\)を固定して、\(z=x+jb \quad (x \in \mathbb R)\)を考えると、\(w = e^z = e^{x + jb} = e^x(\cos b + j \sin b)\)となる。この場合、偏角が\(b\)で固定され、絶対値\(e^x\)が正の実数の範囲で変化するので、\(z\)が\(y=b\)上を右方向に移動すると(図1(左)の青線)、\(w\)は原点から伸びる半直線上を原点から遠ざかる方向に移動することになる(図1(右)の青線)。また、\(b\)の大小が半直線の向きを決定することになる。
2.色相で偏角を表現する(ドメイン・カラーリング)
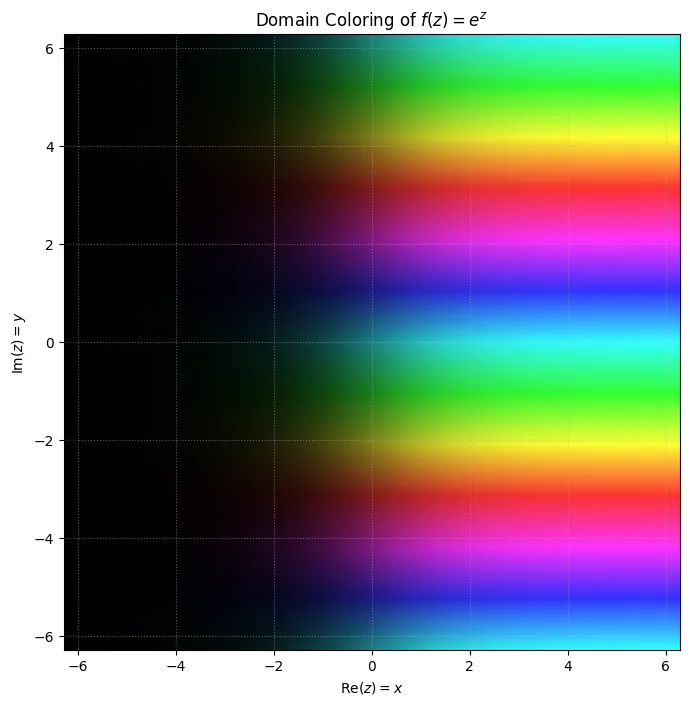
これは、コンピュータグラフィックスを活用した、現代的で直感的な可視化手法である(図2参照)。この手法では、以下のような表現法を使う。
*値の絶対値を高さや明るさで表現:関数 \(w = f(z)\) の絶対値 \(|w|\)を、グラフの高さや色の明るさで表現する。
*値の偏角(位相)を色相で表現:関数 \(w = f(z)\) の偏角\(\arg(w)\) を、色の色相(赤、黄、緑、青など)で表現する。
これにより、複素平面上の各点\(z\)における関数の出力\(w = e^z\)の「大きさ」と「向き」を同時に視覚化できる。
この手法の特徴としては、偏角\(\arg(w)\)は\(2\pi\)ごとに繰り返すため、グラフの色は周期的に変化する。\(e^z\)の場合は、\(y\)軸に沿って移動すると偏角が変化し、色の帯が無限に繰り返される様子が見える(これが\(e^z\)の周期性\(e^{z+2\pi j} = e^z\) を示している)。
対数関数
正の数\(a\)にたいし,方程式\(e^x = a\)の実数解を\(\log a\)と表し,これを\(a\)の対数とよぶ。同じことを複素数で考える。定義を以下に示す。
定義(複素数の対数)
複素数\(\alpha \neq 0\)にたいし、方程式\(e^z = \alpha\)の解を\(\alpha\)の対数とよび、\(\log \alpha\)で表す。
複素数の対数関数\(\log z\)は、指数関数の逆関数として定義される。
複素数\(z\)を極形式で表すと、\(z = r e^{j\theta}\)である。ここで、\(r = |z|\)は絶対値、\(\theta = \arg(z)\)は偏角。このとき、複素対数関数\(\log z\)は、次のように定義できる。$$\log z = \log |z| + j \arg(z)$$ただし、複素数の偏角 \(\arg(z)\)は、\(2\pi\) の整数倍だけ異なっても同じ複素数を表すため、多価関数となる。\(\arg(z) = \theta_0 + 2n\pi \quad (n \text{は任意の整数})\) なので、複素対数の一般的な解は、$$\log z = \log |z| + j(\theta_0 + 2n\pi)$$となる。つまり、複素数の対数は、虚軸に平行な直線上に等間隔\(2 \pi j\)で整然と並ぶことになる。
複素平面上で\(\log z\)はタテ線の上に\(2 \pi j\) 間隔で並んでいるが、その中から\(0 \leq Im (\log z) < 2 \pi\)を満たすものはひとつだけなので、これを\(\log z\) の主値とよび\(\text{Log}\; z\)と表す。
【例】\(\log(-1)\)を求める。
方程式\(e^z = -1\)を解けばよい。指数関数の周期性を考慮すると$$ -1 =e^{j \pi} = e^{j \pi + 2m j \pi} \quad (m \in \mathbb Z)$$ \(e^z\)と比較して、\(z = j(2m+1)\pi \quad (m \in \mathbb Z)\)である。従って、$$\log(-1) = j(2m +1)\pi \quad (m \in \mathbb Z)$$ 主値は、\(\text{Log}(-1) = j \pi\)である。
【例】\(\log(1+j)\)を求める。
方程式\(e^z = 1+ j\)の複素数解を考える。$$e^z = 1 + j = \sqrt{2} e^{j \pi /4} = e^{\log{\sqrt{2}}}\cdot e^{ j \pi/4 + 2 m \pi j} = e^{\log{\sqrt{2}} + j(\pi /4 + 2m \pi) } \quad (m \in \mathbb Z)$$なので、\(z = \log2 / 2 + j(\pi /4 + 2 m \pi) \quad (m \in \mathbb Z)\)。 よって、$$ \log(1+j) = \frac{\log 2}{2} + j \left(\frac{\pi}{4} + 2 m \pi \right) \quad (m \in \mathbb Z)$$である。主値は、$$\text{Log}(1+j) = \frac{\log 2}{2} + j \frac{\pi}{4}$$である。

