1. スライディングモード制御の基本
スライディングモード制御の基本的な考え方として、式(1)で示す二次系システムを考える。$$\dot x = y \\ \dot y = 2y - x +u \\ u = -\phi x \;\;\; \cdots (1)$$ また、式(2)の変数\(\sigma(x,y)\)を導入する。$$\sigma(x,y) = xS, \quad S = 0.5x + y \;\;\; \cdots (2)$$ここで、フィードバックゲインを式(3)のように選ぶ。$$\phi = \left\{ \begin{array}{} 4 & \sigma(x,y) \gt 0 \\ -4 & \sigma(x,y) \lt 0 \end{array} \right. \;\;\; \cdots (3)$$このときの閉ループシステムのブロック線図は図1となる。
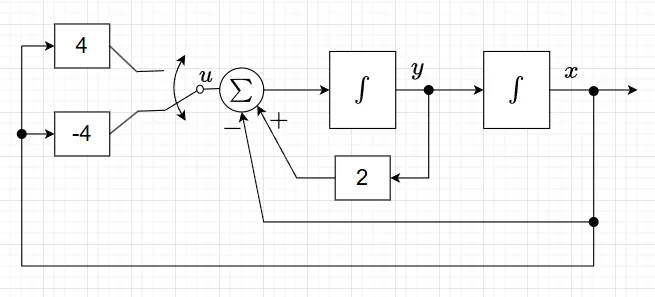
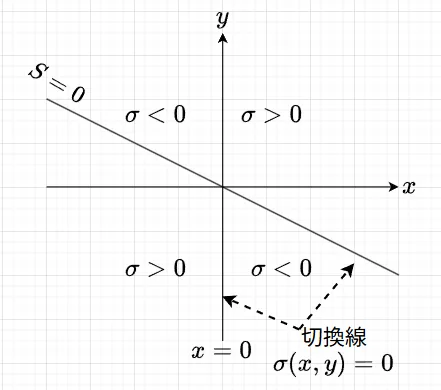
式(2)の変数\(\sigma(x,y)\)は、2つの関数の積で、\(\sigma(x,y)=0\)のとき、$$x=0 \text{または、} S=0.5x + y=0 \;\;\; \cdots (4)$$となる。従って、この二つの関数は、図2に示すように、位相平面を\(\sigma(x,y)\)の符号が異なるように分割する。これより、式(4)を切換線と呼ぶ。また、\(\sigma(x,y)\)を切換関数と呼ぶ。切換線は、位相空間の次数が高くなると切換線から切換面になり、さらに幾何学的に図示できなくなる超平面になる。フィードバックゲインは、\(\sigma(x,y)\)の符号によって切り換えられる。従って、式(1)は、位相平面の二つの領域において、二つの微分方程式によって定義される。
領域Ⅰ \(\sigma(x,y) = xS \gt 0 \) のとき、$$ \dot x = y \\ \dot y = 2y - x - 4x = 2y - 5x \;\;\; \cdots (5)$$
領域Ⅱ \(\sigma(x,y) = xS \lt 0 \) のとき、$$ \dot x = y \\ \dot y = 2y -x +4x = 2y +3x \;\;\; \cdots (6)$$
※式(5)、式(6)による位相平面軌跡を描くPythonスクリプトを示す。
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# Define sigma(x, y)
def sigma(x, y):
S = 0.5 * x + y
return x * S
# Define the switched dynamics
def switched_dynamics(t, state):
x, y = state
sig = sigma(x, y)
dxdt = y
if sig > 0:
dydt = 2 * y - 5 * x # Region I
else:
dydt = 2 * y + 3 * x # Region II
return [dxdt, dydt]
# Time settings
t_span = [0, 10]
t_eval = np.linspace(t_span[0], t_span[1], 1000)
# Initial conditions
initial_conditions = [
[0.0, 1.0], [0.0, -1.0], [0.0, 2.0], [0.0, -2.0], [0.0, -3.0], [0.0, 3.0],
[1.0, 0.0], [-1.0, 0.0], [1.0, -2.0], [-1.0, 2.0],
[2.0, -2.0], [-2.0, 2.0], [2.0, -3.0], [-2.0, 3.0]
]
# Create the plot
plt.figure(figsize=(10, 6))
for x0, y0 in initial_conditions:
sol = solve_ivp(switched_dynamics, t_span, [x0, y0], t_eval=t_eval)
x_vals, y_vals = sol.y
plt.plot(x_vals, y_vals, label=f"IC=({x0},{y0})")
# Add arrows along the trajectory to show direction
for i in range(0, len(x_vals) - 1, 50): # Plot every ~50 steps
dx = x_vals[i+1] - x_vals[i]
dy = y_vals[i+1] - y_vals[i]
plt.arrow(x_vals[i], y_vals[i], dx, dy
head_width=0.2, head_length=0.3, fc='k', ec='k')
plt.title("Trajectories with Switching Dynamics and Direction Arrows")
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.axis('equal')
plt.legend()
plt.show()
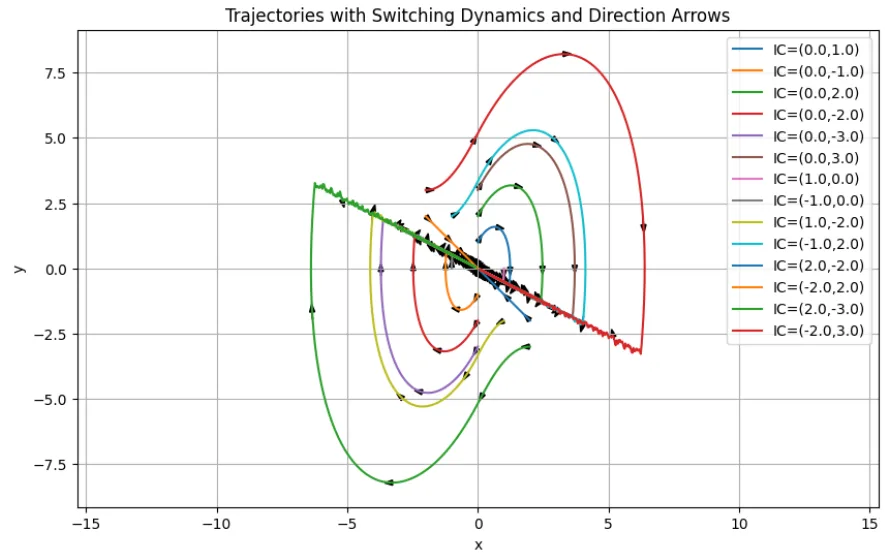
(\(S\)の傾きが小さい場合)
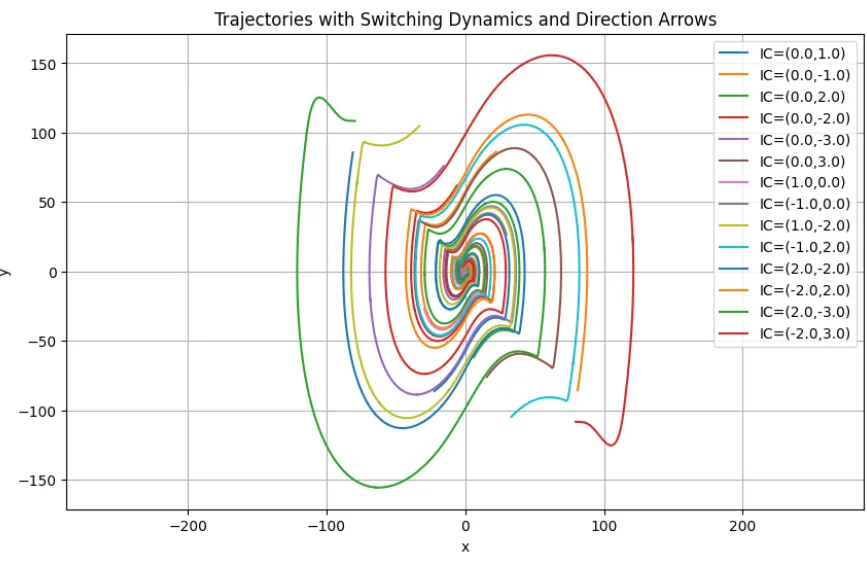
(\(S\)の傾きが大きい場合)
図3の位相平面上の軌跡から分かるように、直線\(S\)は直線の両側から来た軌跡の終点となっている。さらに、状態(\(x,\;y\))はこの直線上に拘束されて、平衡点(原点)に滑っていくことになる。この滑り状態がスライディングモードと呼ぶ運動を表している。
切換線\(S\)の傾きを大きくした場合は、図4のようにスライディングモードにはならずスパイラル状になって原点に収束する。それでも不安定な系は、漸近安定となって安定化される。
以上のように、スライディングモードが起こる場合は、システムの位相空間上での挙動は二つのモードに分けられる。一つは到達モードで、非スライディングモードである。このモードでは、位相平面上の任意の場所(図の初期値 IC)から出発した軌跡は、切換線に向かって動き、有限時間で切換線に到達する。もう一つは、スライディングモードで、微分方程式 $$ S = 0.5x+y =0.5x + \dot x =0 \;\;\; \cdots (7)$$で定義されるように\(S=0\)の切換線上で、\(x,y\)の軌跡は原点に漸近的に近づく。
このスライディングモード制御系から、以下の四つの基本的な視点が与えられる。
1)位相平面上の原点はシステムの平衡状態を表すので、スライディングモードはシステムの過渡的な期間中の挙動を示していることになる。従って、直線\(S\)はスライディングモード中のシステムの過渡応答を定義していることになる。
2)スライディングモード中、軌跡のダイナミクスの式(7)は元のモデルの式(1)より低い次数となる。
3)スライディングモード中、システムのダイナミクスは、直線\(S\)を記述するパラメータだけに支配される。
4)スライディングモードは、式(5)、式(6)によって定義される二つの構造のどちらとも独立した軌跡である。
制御の過程中、制御システムの式(1)は、一つの制御構造である式(5)から別の制御構造の式(6)へ変わることになる。このことから、可変構造制御と呼ぶこともできる。しかし、ここでの制御系はスライディングモード状態が重要なので、スライディングモード制御と呼ぶ。
スライディングモード制御問題
スライディングモード制御問題は以下のように記述できる。
制御系を式(8)の状態方程式で表す。$$ \dot x = A(x,t) + B(x,t) u \;\;\; \cdots (8)$$ここで、\(x\)と\(u\)は\(n\)次と\(m\)次のベクトルで、\(x \in R^n,\quad u \in R^m\)で表す。このとき、
1)\(\sigma(x)\)のようなベクトル表現で、\(m\)個の切換関数が表される。
2)可変構造制御は式(9)で表される。$$u(x,t) = \left\{ \begin{array}{} u^{+}(x,t) & \sigma(x) \gt 0 \\ u^{-}(x,t) & \sigma(x) \lt 0 \end{array} \right. \;\;\; \cdots(9)$$もし、到達条件を満足していれば、到達モードは有限時間で集合\(\sigma(x)=0\)(切換面)に到達する。このことより、スライディングモード制御の実現には、以下の手順が必要となる。
1)与えられたプラント(制御対象)より低次数、一般には\(n-m\)次元の望ましいシステムダイナミクスを表すための切換面\(\sigma(x) = 0\)を設計する。
2)切換面の外にあるどのような状態\(x\)でも、有限時間で切換面に到達するような可変構造制御入力\(u(x,t)\)を設計する。


“1. スライディングモード制御の基本” に対して1件のコメントがあります。
コメントは受け付けていません。