30. インピーダンス制御

インピーダンス制御（Impedance Control）は、ロボットの先端（エンドエフェクタ）と環境との間の「動的な関係（力と運動の関係）」を操るための制御手法である。これまでの「位置制御」や「力制御」とは異なり、ロボットに「仮想的なバネ・マス・ダンパ系（機械インピーダンス）」の性質を持たせることが最大の特徴となっている。ロボットやメカトロ系が「どれくらい柔らかく／硬く振る舞うか」を制御する手法といえ、人と接触するロボットや力制御の中核技術となっている。
インピーダンス制御は、機械システムのインピーダンスパラメータ（慣性、粘性、剛性パラメータで、それぞれ力と加速度、速度、変位の比に対応）を目標値に保つ制御を意味し、アクチュエータで駆動される機構が対象に作用を及ぼす際、対象に加わる変位、速度、加速度を検知しつつ、対象との間の相互作用力がある関係を維持するようにアクチュエータの発生力を制御する。

機械インピーダンスの基本

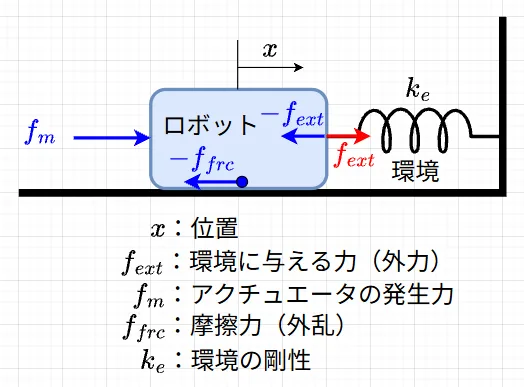
ロボットが環境に与える力を\(f_{ext}\)としたとき、目標軌道\(x_d\)と実際の軌道\(x\)の関係より式(1)が成り立つ。$$M(\ddot{x} - \ddot{x}_d) + D(\dot{x} - \dot{x}_d) + K(x - x_d) = f_{ext} \quad \cdots (1)$$・\(M\)(慣性/質量)：重さ（加速のしにくさを決める。)
・\(D\) (粘性/ダンパ)：摩擦（動きのしなやかさを決める。)
・\(K\) (剛性/バネ)：硬さ（押し返そうとする力を決める。)
これらの値をプログラム上で自由に変えることで、同じロボットのアクチュエータを「硬直的構造体」にしたり、「柔軟構造体」にしたりできる。
式(1)を\(\ddot{x}\)について解くと、式(2)と表せる。$$\ddot{x} = \ddot{x}_d +\frac{1}{M}\left\{f_{ext} - D(\dot{x} - \dot{x}_d) - K(x - x_d)\right\} \quad \cdots (2)$$ この\(\ddot{x}\)は、「あらかじめ決めていた目標加速度」の\(\ddot{x}_d\)と異なり、「外乱を含めて、インピーダンス特性を実現するために今すぐ出すべき修正後の加速度指令」となる。つまり、\(\ddot{x}_d\)が外力が全くないときに、ロボットが本来たどるべき予定の加速度（例：台形加速で動かす、など）であり、\(\ddot{x}\)は、外力\(f_{ext}\)が加わったとき、バネ・マス・ダンパの法則に従って「軌道をどれだけ修正すべきか」を計算した結果の、制御器への最終的な指令値である。
この\(\ddot{x}\)を加速度制御系の加速度指令値とすればよい。

１自由度質点モデルに対するインピーダンス制御のシミュレーション

基本的な 1自由度質点モデル に対してインピーダンス制御を適用するScilabスクリプトを以下に示す。途中で外力（壁への接触など）が発生した際の挙動を確認する。
target_pos(t)でロボットの本来の軌道を定義している。external_force(t, x)関数で、位置が 0.3m を超えたときに押し戻される力を仮定している。impedance_model(t, y)内で、偏差に対して指定した\(M_m, B_m, K_m\)の特性が出るように加速度accを決定している。
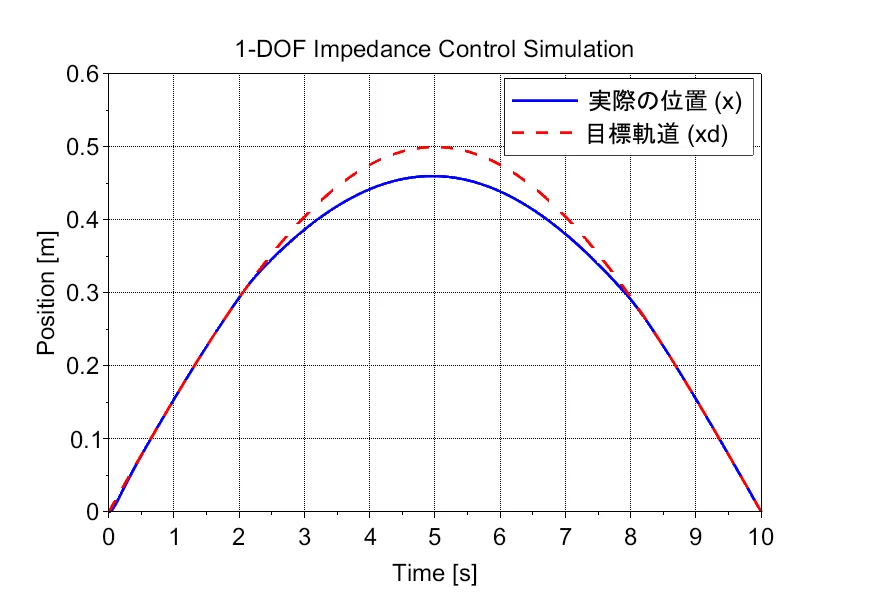
シミュレーション結果では、非接触時（\(x \le 0.3\) m の位置）においてロボットは目標軌道（赤の点線）に追従する。接触時（\(x > 0.3\) m）においては、 壁からの反力\(f_{ext}\)により、目標軌道から押し戻される。この際、剛性\(K_m\)を小さくするとより「柔らかく」なり押し戻される量が大きくなる。剛性\(K_m\)を大きくすると「硬く」なり押し込む様子が確認できる。
インピーダンス制御の本質は、この 「偏差を許容し、その際の力学的関係を設計する」 点にあるといえる。

// インピーダンス制御シミュレーション (1自由度)
clear; clc;
// パラメータ設定
M_m = 2.0; // 質量 [kg]
B_m = 40.0; // 粘性 [Ns/m]
K_m = 200.0; // 剛性 [N/m]
// 目標軌道と外力の設定
function xd = target_pos(t)
　xd = 0.5 * sin(2 * %pi * 0.05 * t); // 0.05Hzの正弦波
endfunction
function f_ext = external_force(t, x)
　if x > 0.3 then
　　f_ext = 50.0 * (x - 0.3); // 0.3m以上の地点に柔らかい壁がある想定
　else
　　f_ext = 0;
　end
endfunction
// 微分方程式の定義
// y(1): 位置 x, y(2): 速度 v
function dydt = impedance_model(t, y)
　x = y(1);
　v = y(2);
　xd = target_pos(t);
　vd = (target_pos(t+0.001) - target_pos(t)) / 0.001; // 近似微分
　ad = (target_pos(t+0.001) - 2*target_pos(t) + target_pos(t-0.001)) / 0.001^2;
　f_ext = external_force(t, x);
// インピーダンス則に基づく加速度の計算
// M_m*(ad - acc) + B_m*(vd - v) + K_m*(xd - x) = f_ext
　acc = ad + (B_m*(vd - v) + K_m*(xd - x) - f_ext) / M_m;
　dydt = [v; acc];
endfunction
// シミュレーションの実行
t = 0:0.01:10;
y0 = [0; 0]; // 初期位置0, 初期速度0
sol = ode(y0, 0, t, impedance_model);
// 結果のプロット
clf();
plot(t, sol(1, :), 'b-', "linewidth", 2);
plot(t, target_pos(t), 'r--', "linewidth", 1);
hl = legend(['実際の位置 (x)'; '目標軌道 (xd)']);
xlabel("Time [s]");
ylabel("Position [m]");
title("1-DOF Impedance Control Simulation");
xgrid();