29. 加速度制御
加速度制御(Acceleration Control)は、精密モーションコントロールの基盤となる技術で、その本質は、複雑な物理特性を持つモータやロボットアームを、「ニュートンの運動方程式(\(F=ma\))通りに動く、理想的な物体」に見なせるようにすることにある。
例えば、モータへの指令値(操作量)は「電流(=トルク)」だが、現実のモータでは摩擦、重力、慣性変動、外乱トルクが影響するため、電流を流しても期待通りの加速度が得られるわけではない。加速度制御の目的は、これらすべての「不要な要素」をリアルタイムで打ち消し、外部からの加速度指令 \(\alpha_r\)に対して、実際の加速度\(\ddot{x}\)が即座に一致する系を構築することである。$$\ddot{x} \approx \alpha_r$$
加速度制御の構成
加速度制御の本質は、実際のシステム(プラント)を近似的に「指令値通りの加速度で動く理想的な二重積分器」にすることである。図1は回転モータに対する加速度制御系の構成ブロック図例である。
角加速度指令値 (\(\ddot{\theta}_r\))は動かしたい目標の角加速度で、単位は\([rad/s^2]\)である。公称慣性 (\(J_n\))は 制御対象の慣性モーメントの公称で、角加速度指令にこれを掛けることで、必要なトルク指令 (\(\tau_r\)) を算出する。図1では、これを\(K_n\)(公称トルク定数)で割ることで、トルクに必要な電流値\(i_c\)を求めている。\(K_t\)は実トルク定数、\(J_t\)は実慣性モーメントである。
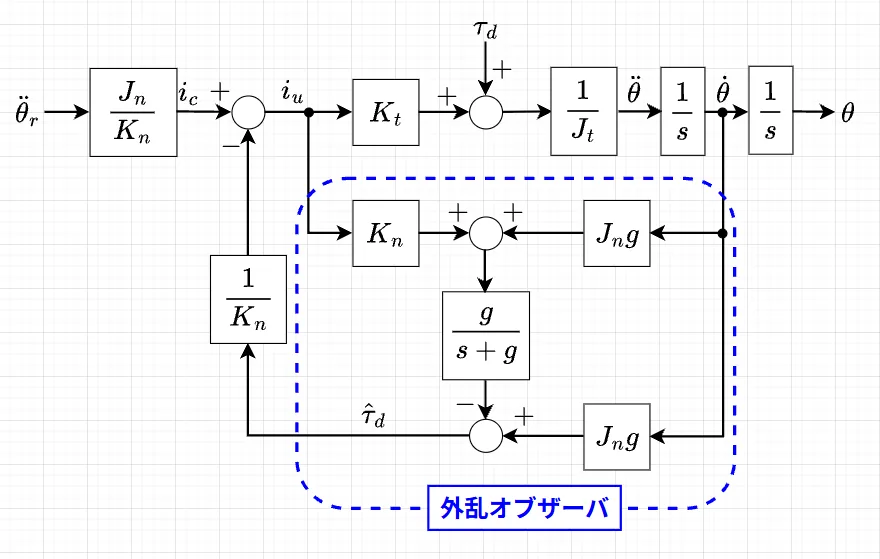
\(\tau_d\)が外乱トルクで、\(\hat{\tau}_d\)が外乱オブザーバにより生成される推定外乱トルクである。\(\hat{\tau}_d\)を\(K_n\)で割ることで、推定外乱トルクに対応した電流となり、これをフィードバックすることで、外乱トルク\(\tau_d\)を打ち消すことができる。これにより、制御対象ををあたかも「摩擦のない理想的な物体」として動作させることができる。
推定外乱トルク\(\hat{\tau}_d\)は式(1)で表せる。$$\hat{\tau}_d = \frac{g}{s+g}\left(J_n s \dot{\theta} - K_n i_u \right) \;\quad \cdots (1)$$ここで、\(\frac{g}{s+g}\)は\(s\dot{\theta}\)により角速度\(\dot{\theta}\)から角速度\(\ddot{\theta}\)を求める際の微分による雑音の影響を抑制するためのローパスフィルタ(Qフィルタ)である。\(g\)は外乱トルクの推定帯域を決めるカットオフ周波数である。
ここで、\(\frac{s}{s+g} = 1 - \frac{g}{s+g}\)の関係を使って、式(1)を変形すると、$$\hat{\tau}_d = \frac{g}{s+g}J_n s \dot{\theta} - \frac{g}{s+g}K_n i_ u \\=\frac{s}{s+g}J_n g \dot{\theta} - \frac{g}{s+g}K_n i_u \\= \left(1 - \frac{g}{s+g}\right) J_n g \dot{\theta} - \frac{g}{s+g} K_n i_u \\=J_n g \dot{\theta} - \left(\frac{g}{s+g} J_n g \dot{\theta} + \frac{g}{s+g}K_n i_u\right) \\ = J_n g \dot{\theta} - \frac{g}{s+g}\left(J_n g \dot{\theta} + K_n i_u\right)$$となる。この構成であれば、「角速度を微分して角加速度を出す」という処理が不要になり、雑音の元となる微分を必要としない形式にできる。この外乱オブザーバにより図1の加速度制御系が構成できる。これにより、上位の制御器(位置制御や速度制御)からは制御対象を、複雑な物理特性を気にせず「加速度\(\alpha_r= \ddot{x}_r\)( 上記の例では、\(\ddot{\theta}_r\))を入力すれば、その通りに動く物体(回転体)として扱うことができるようになる。
モータの加速度制御シミュレーション
図1に従って、モータの加速度制御シミュレーションを考える。
・モータ(プラント): 電流\(i_u\)に対してトルク\(T = K_t \cdot i_u\)を発生し、慣性\(J\)を回転させる。
・加速度制御: 目標加速度(角加速度)\(a_ref\) に公称慣性\(J_n\)を掛けて、トルク定数\(K_n\)で割ることで、電流指令値を生成する。
・DOB(外乱オブザーバ): 実際の速度\(v\)から外乱を推定し、電流指令に補正を加える。
Sclilabによるシミュレーションスクリプトを下記に示す。
// --- パラメータ設定 ---
dt = 0.001; // サンプリング時間 [s]
T_end = 1.0; // シミュレーション時間 [s]
t = 0:dt:T_end;
J = 0.02; // 実際の慣性 [kg・m^2]
Jn = 0.02;// 公称慣性 [kg・m^2]
Kt = 0.5; // トルク定数 [Nm/A]
g = 100; // DOB帯域(カットオフ周波数) [rad/s]
// --- 変数初期化 ---
v = 0; //実速度
a_ref = 10; //加速度指令値 [rad/s^2]
dist = 1.0; // 外乱トルク [Nm](0.5sで発生)
xi = 0; // DOB内部の状態変数(積分用)
v_history = zeros(t);
a_history = zeros(t);
d_hat_history = zeros(t);
tau_ref = 0; // ループ内で更新
for i = 1:length(t)
curr_t = t(i);
// 1. 目標加速度(0.2sからステップ状で加速)
ref_acc = (curr_t > 0.2) * a_ref;
// 2. 外乱オブザーバ
// 状態変数 xi を用いた微分器なしの実装
d_hat = xi + g * Jn * v;
// xi の微分値: d(xi)/dt = -g*xi - g^2*Jn*v - g*tau_ref
xi = xi + dt * (-g * xi - g * g * Jn * v - g * tau_ref);
// 3. トルク指令の生成
// 外乱 d_hat は「逆方向の力」として推定されるため、
// それを「差し引く(マイナスする)」ことで打ち消し(補正)を行う
tau_acc = ref_acc * Jn;
tau_ref = tau_acc - d_hat; // 補正:マイナスにする
// 4. プラント(実際のモータ)の挙動
d_actual = (curr_t > 0.5) * dist; // 0.5秒から外乱トルク発生
acc = (Kt * (tau_ref / Kt) - d_actual) / J;
v = v + dt * acc;
// 記録
v_history(i) = v;
a_history(i) = acc;
d_hat_history(i) = d_hat;
end
// --- グラフ描画 ---
clf();
subplot(2,1,1);
plot(t, a_history, "r");
hl=legend(["Actual Acceleration"]);
xtitle("Acceleration Response (Corrected)", "Time [s]", "Acc [rad/s^2]");
subplot(2,1,2);
plot(t, v_history, "b");
xtitle("Velocity Response", "Time [s]", "Vel [rad/s]");
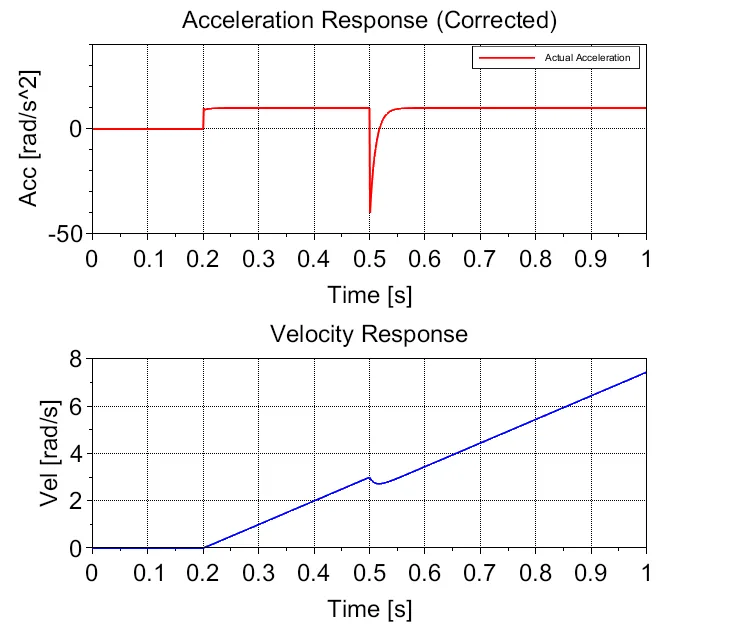
シミュレーション(Scilab)
図2がシミュレーション結果で、0.2 s の時点で目標加速度(角加速度)をステップ状に与えている。これにより、定加速度でモータ速度(角速度)が上昇している。0.5 s の時点で外乱トルク1.0 Nm(加速度:50 rad/s^2)が加わると加速度が大きく変化するが、DOBにより一瞬の乱れの後、すぐに元の定加速度に戻る。0.5 s 時点で速度も一瞬変化するが、その後の速度は直線的に増え続ける。


“29. 加速度制御” に対して1件のコメントがあります。
コメントは受け付けていません。