40. 実積分への応用（複素関数）

積分計算の手順

\(I=\int_C f(z) dz \)を計算する。
１）\(f(z)\)の極で\(C\)の内部にあるもの\(\alpha_1,\alpha_2,\cdots,\alpha_n\)を求める。
２）留数\(\text{Res}(f(z),\;\alpha_k)\)を計算する。
３）\(I = 2 \pi j \sum_{k=1}^n \text{Res}(f(z),\;\alpha_k)\)を計算する。

実積分への応用（三角関数の積分）

$$I = \int_0^{2\pi} \frac{1}{5 + 3 \cos \theta} d\theta$$を求める。
\(z = e^{j\theta}\)とおき、単位円\(|z|=1\)上の積分に変換する。\(dz = j e^{j\theta} d\theta = j z d\theta\) なので、\(d\theta = \frac{dz}{jz}\)となる。また、\(\cos \theta = \frac{e^{j\theta} + e^{-j\theta}}{2}\)なので、\(\cos \theta = \frac{z + z^{-1}}{2} = \frac{z^2 + 1}{2z}\)となる。これらを積分に代入し、積分路を \(C: |z|=1\) (単位円) とする。従って、$$I = \int_C \frac{1}{5 + 3 \left(\frac{z^2 + 1}{2z}\right)} \cdot \frac{dz}{jz} \\= \frac{2}{j} \int_C \frac{1}{3z^2 + 10z + 3} dz$$被積分関数を\(f(z)\)とすると、$$f(z) = \frac{1}{3z^2 + 10z + 3} = \frac{1}{3(z+1/3)(z+3)}$$なので、単位円内の極は、\(z=-1/3\)のみである。よって、留数定理より、$$I = \frac{2}{j}\cdot 2 \pi j \cdot \text{Res}\left(f(z),\;-\frac{1}{3}\right)$$となる。ここで、「留数の計算公式１」を使うと、\(f(z)\)の極\(z=-1/3\)の位数は\(k=1\)なので、$$\text{Res}\left(f(z),\; -\frac{1}{3} \right) = \left. \frac{1}{3(z+3)}\right|_{z=-\frac{1}{3}} = \frac{1}{8}$$以上より、$$I = \frac{2}{j}\cdot 2\pi j \cdot \frac{1}{8} = \frac{\pi}{2}$$となる。

実積分への応用（有理関数の積分：広義積分）

$$I = \int_{-\infty}^{\infty} \frac{1}{1 + x^4}dx$$を求める。

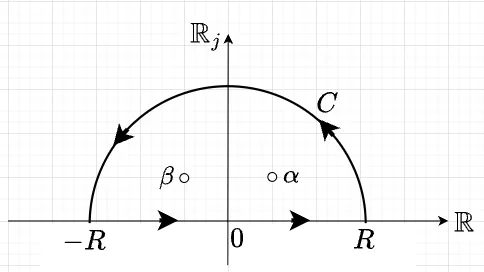
極は分母が\(0\)になるところなので、\(1 + z^4 = 0\)の解で、$$z^4 = -1 = e^{j(\pi + 2k\pi)}, \quad k \in \mathbb{Z}$$なので、極\(z_k\) は、\(-1\)の4乗根として得られる。$$z_k = e^{j\frac{\pi + 2k\pi}{4}}, \quad k = 0, 1, 2, 3$$上半平面（\(\mathrm{Im}(z) > 0\)）にある極は \(\alpha\) と\(\beta\)である。$$\alpha = e^{j \frac{\pi}{4}} = \frac{1}{\sqrt{2}} + j \frac{1}{\sqrt{2}}, \quad \beta =e^{j\frac{3 \pi}{4}}= -\frac{1}{\sqrt{2}} + j \frac{1}{\sqrt{2}}$$
\(C\)内の極は、\(\alpha, \; \beta\)なので、\(f(z) = \frac{1}{1 + z^4}\)にたいする線積分は、$$\int_C = \int_C \frac{1}{1 + z^4} = 2 \pi j \cdot \left\{\text{Res}\left(\frac{1}{1 + z^4},\; \alpha\right) + \text{Res}\left(\frac{1}{1 + z^4},\; \beta \right)\right\}$$となる。 ここで、「留数の計算公式２」を使うと、$$\text{Res}\left(\frac{1}{1 + z^4},\; \alpha \right) = \frac{1}{4 \alpha^3} = \frac{e^{-3\pi j/4}}{4} = \frac{-1-j}{4 \sqrt{2}} \\ \text{Res}\left(\frac{1}{1 + z^4},\; \beta \right) = \frac{1}{4 \beta^3} = \frac{e^{-9\pi j/4}}{4} = \frac{1-j}{4 \sqrt{2}}$$となるので、$$\int_C = 2 \pi j \left(\frac{-1-j}{4 \sqrt{2}} + \frac{1-j}{4 \sqrt{2}} \right) = \frac{\pi}{\sqrt{2}}$$である。
ここで、経路\(C\)を次のように分割する。$$J_R := \{z = x | -R \leq x \leq R\} , \quad C_R := \{z = Re^{j \theta} | 0 \leq \theta \leq \pi \} , \quad C = J_R + C_R$$このとき、$$\int_C = \int_{J_R} + \int_{C_R} = \frac{\pi}{\sqrt{2}}$$なので、$$\lim_{R \to \infty} \int_{C_R} f(z) dz = 0 \quad \text{　であれば、} I = \lim_{R \to \infty} \int_{J_R} = \frac{\pi}{\sqrt{2}}$$を得る。
$$\lim_{R \to \infty} \int_{C_R} f(z) dz = 0$$は、以下で証明される。
\(|z| = R>1\)のとき、$$|z^4 +1| \geq |z|^4 -1 =R^4 -1 >0$$であるから、\(C_R\)上\(|f(z)| \leq \frac{1}{R^4 -1}\)が成立する。よって、$$\left|\int_{C_R} f(z) dz \right| \leq \frac{l(C_R)}{R^4 -1} = \frac{\pi R}{R^4 -1} \to 0 \quad (R \to \infty)$$である。
以上より、$$I = \int_{-\infty}^{\infty} \frac{1}{1 + x^4}dx = \frac{\pi}{\sqrt{2}}$$である。

実積分への応用（複雑な関数の広義積分）

広義積分 $$I = \int_{-\infty}^{\infty} \frac{\cos x}{1+x^2} dx$$ を留数定理を用いて求める。

被積分関数を複素関数に拡張する際に、\(\cos x\)を\(e^{jx}\)の実部として扱う。$$I = \mathrm{Re} \left\{ \int_{-\infty}^{\infty} \frac{e^{jx}}{1+x^2} dx \right\}$$複素関数\(f(z)\)を次のように定義して、$$f(z) = \frac{e^{jz}}{1+z^2}$$線積分\(\int_C = \int_C f(z)dz\)を考える。ここで、積分経路\(C\)は、前問と同様に図１を使う。つまり、実軸上の区間 \([-R, R]\) と、上半平面の半円 \(C_R: |z|=R, \mathrm{Im}(z) \ge 0\)を合わせた閉じた積分路\(C\)を考え、\(R \to \infty\)の極限をとる。\(C\)内の極は\(z=j\)のみなので、$$\int_C = 2 \pi j \cdot \text{Res}(f(z),\; j)$$となる。いま、\(f(z) = \frac{1}{z-j}\cdot \frac{e^{jz}}{z+j}\)であり、\(\frac{e^{jz}}{z+j}\)は\(z=j\)において正則なので、「留数の計算公式１」を使い、$$\text{Res}(f(z),j) = \frac{e^{j \cdot j}}{j + j} = \frac{e^{-1}}{2j}$$となる。よって、$$\int_C = 2 \pi j \cdot \frac{e^{-1}}{2j} = \frac{\pi}{e}$$となる。ここで、\(\lim_{R \to \infty} \int_{C_R} f(z) dz = 0\)を考える。 \(|z| = R>1\)のとき、\(|z^2 +1| \geq |z|^2 -1 =R^2 -1>0\)が成り立つ。さらに、\(z = x +j y \in C_R\)とおくと、\(y \geq 0\)より、$$|e^{jz}| = |e^{j(x+jy)}| = |e^{jx}||e^{-y}|=1 \cdot e^{-y} \leq 1$$である。よって、\(C_R\)上で、$$|f(z)| = \left|\frac{e^{jz}}{1+z^2}\right| \leq \frac{1}{R^2 -1}$$が成り立つ。よって、$$\left|\int_{C_R} f(z) dz \right| \leq \frac{l(C_R)}{R^2 -1} = \frac{\pi R}{R^2 -1} \to 0 \quad (R \to \infty)$$となる。
$$\int_{J_R} = \int_{-R}^R\frac{e^{jx}}{1+x^2}dx = \int_{-R}^R \frac{\cos x}{1+x^2} dx + j \int_{-R}^R \frac{\sin x}{1+x^2} dx$$であるが、\(\frac{\sin x}{1+x^2}\)は奇関数なのでこの積分の虚部は０となる。以上より、$$I =\int_{-\infty}^{\infty} \frac{\cos x}{1+x^2} dx =\lim_{R \to \infty} \int_{J_R} = \int_C =\frac{\pi}{e}$$となる。