39. 留数定理(複素関数)
定理:ローラン展開
\(\alpha \in \mathbb{C}\)とし、円環領域\(D = \{z \in \mathbb{C}\;|\; R_1 <|z - \alpha| < R_2\} \)上で関数\(f : D \to \mathbb{C}\)は正則であるとする。また、\(n \in \mathbb{Z}\)および\(C = C(\alpha,R),\;(R_1 < R < R_2)\)にたいし、$$a_n := \frac{1}{2 \pi j}\int_C \frac{f(z)}{(z - \alpha)^{n+1}}dz$$と定める。このとき、任意の\(z \in D\)にたいして、以下の等式が成り立ち、これを\(f(z)\)の\(\alpha\)におけるローラン展開とよぶ。$$f(z) = \sum_{n=-\infty}^{\infty} a_n(z - \alpha)^n \\= \cdots + \frac{a_{-2}}{(z - \alpha)^2} + \frac{a_{-1}}{z - \alpha} + a_o + a_1(z - \alpha) + a_2(z - \alpha)^2 + \cdots $$
※ここで、\(f(z) = f(z)_1 + f(z)_2\)とし、$$f(z)_1 = \cdots + \frac{a_{-2}}{(z - \alpha)^2} + \frac{a_{-1}}{z - \alpha} \\f(z)_2 = a_o + a_1(z - \alpha) + a_2(z - \alpha)^2 + \cdots$$とする。
ローラン展開において、\(f(z)_1\)と\(f(z)_2\)の級数はそれぞれ収束し、その和が左辺\(f(z)\)に一致する。
また、\(f(z)\)が穴あき円板\(D = \{z \in \mathbb{C}\;|\; R_1 <|z - \alpha| < R_2\} \)で正則であり、さらにある自然数\(k\)と\(a_{-k} \neq 0\)が存在して、$$f(z) = \frac{a_{-k}}{(z - \alpha)^k} + \cdots + \frac{a_{-1}}{z - \alpha} + a_o + a_1(z - \alpha) + a_2(z - \alpha)^2 + \cdots $$とローラン展開であるとき、\(f(z)\)は\(z = \alpha\)において\(k\)位の極を持つという。
※ローラン展開において、\(a_{-k} \neq 0\)を満たす\(k\)が無限に存在するとき、\(\alpha\)は極とよばれず、真性特異点とよばれる。一般には極と真性特異点を合わせて特異点とよばれる。
【ローラン展開の証明】
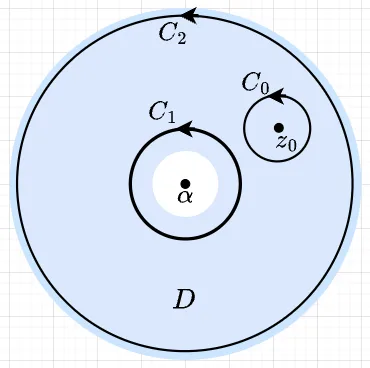
\(z_0 \in D\)を固定する。また、十分小さな\(\epsilon >0\)をとることで、\(C_0=C(z_0,\epsilon)\)は\(D\)の内部にあるとしてよい。さらに、\(r_1,\; r_2 > 0\)を\(R_1 < r_1 < r_2 < R_2\)となるように選んで、図1のように\(C_0,C_1 = C(\alpha,r_1),C_2=C(\alpha,r_2)\)が互いに交わらないようにできる。このときコーシーの積分定理より、$$\int_{C_0} \frac{f(z)}{z - z_0}dz = \int_{C_2} - \int_{C_1}$$が成り立つ。
積分公式より、\(f(z_0) = \frac{1}{2 \pi j}\int_{C_0}\)なので、以下を証明する。
1)\(f(z)_1\)部分:$$-\frac{1}{2 \pi j}\int_{C_1} = \sum_{m \geq 1} a_{-m}(z_0 - \alpha)^{-m}, \quad a_{-m} = \frac{1}{2 \pi j}\int_C \frac{f(z)}{(z - \alpha)^{-m+1}}dz$$\(z \in C_1\)のとき、\(|z - \alpha| < |z_0 - \alpha|\)なので$$-\frac{1}{2 \pi j}\int_{C_1} = \frac{1}{2 \pi j}\int_{C_1} \frac{z}{z_0 - \alpha} \cdot \frac{1}{1 - \frac{z - \alpha}{z_0 - \alpha}}dz = \frac{1}{2 \pi j} \int_{C_1} \frac{f(z)}{z_0 - \alpha} \sum_{n \geq 0} \left(\frac{z - \alpha}{z_0 - \alpha}\right)^n dz \\ = \frac{1}{2 \pi j}\int_{C_1} \sum_{n \geq 0}\left(\frac{f(z)}{(z - \alpha)^{-n}}\cdot \frac{1}{(z_0 - \alpha)^{n+1}}\right)dz \\ = \frac{1}{2 \pi j}\sum_{n \geq 0}\left(\int_{C_1} \frac{f(z)}{(z - \alpha)^{-n}}dz \right)\cdot \frac{1}{(z_0 - \alpha)^{n+1}} \\ = \sum_{n+1 = m \geq 1}\left(\frac{1}{2 \pi j}\int_{C_1} \frac{f(z)}{(z - \alpha)^{-m+1}}dz \right)\cdot (z_0 - \alpha)^{-m}$$ここで、積分路\(C_1\)は、積分定理により\(C\)に変えてよいので、\(f(z)_1\)部分が得られる。
2)\(f(z)_2\)部分:$$\frac{1}{2 \pi j}\int_{C_2} = \sum_{n \geq 0} a_n(z_0 - \alpha)^n, \quad a_n = \frac{1}{2 \pi j}\int_C \frac{f(z)}{(z - \alpha)^{n+1}}dz$$この計算は、テイラー展開と同様となり、正則部分(テイラー展開部分)とよばれる。
ローラン展開の具体例
1.関数\(\frac{e^z}{z^2}\)をローラン展開する。
\(D = \{0 < |z| < \infty\}\)で正則なので、ローラン展開できる。
関数\(e^z\)は\(z=0\)の周りで正則なので、次のマクローリン級数(テイラー級数)に展開できる。$$e^z = \sum_{n=0}^{\infty} \frac{1}{n!} z^n = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \frac{z^4}{4!} + \cdots$$この級数は、複素平面全体(\(|z| < \infty\))で収束する。
よって、$$\frac{e^z}{z^2} = \frac{1}{z^2}\left(1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \cdots\right) = \frac{1}{z^2} + \frac{1}{z} + \frac{1}{2!} + \frac{z}{3!} + \cdots \\ =\sum_{n=-2}^{\infty} \frac{1}{(n+2)!} z^n \quad (0 < |z| < \infty)$$\(z=0\)は2位の極である。
2.関数\(\frac{1}{z^2(z-2)}\)をローラン展開する。
\(D = \{0 < |z| < 2\}\)で正則なので、ローラン展開できる。
まず、\(\frac{1}{z-2}\)を\(z=0\)の周りでテイラー展開する。\(|z| < 2\) なので、\(\left|\frac{z}{2}\right| < 1\)なので、$$\frac{1}{z-2} = \frac{1}{-2(1 - \frac{z}{2})} = -\frac{1}{2} \cdot \frac{1}{1 - \frac{z}{2}}$$と変形できる。等比級数の公式を適用すると、$$\frac{1}{1 - \frac{z}{2}} = \sum_{n=0}^{\infty} \left(\frac{z}{2}\right)^n = 1 + \frac{z}{2} + \frac{z^2}{4} + \frac{z^3}{8} + \cdots$$となる。従って、$$\frac{1}{z^2(z-2)} = \frac{1}{z^2}\cdot \frac{1}{-2(1 - z/2)} = -\frac{1}{2z^2}\cdot \left(1+ \frac{z}{2} + \frac{z^2}{4} + \cdots \right) \\ = -\frac{1}{2z^2} - \frac{1}{4z} - \frac{1}{8} - \frac{z}{16}- \cdots = \sum_{n=-2}^{\infty} -\frac{1}{2^{n+3}} z^n$$\(z=0\)は2位の極である。
留数
基本公式
1.\(m \in \mathbb{Z}, \; C=C(\alpha,\;r)\)とするとき、\(r>0\)の値によらず、$$\int_C (z - \alpha)^m dz = \begin{cases} 0 & (m \neq -1) \\ 2 \pi j & (m=-1) \end{cases}$$が成り立つ。
2.任意の単純閉曲線\(C\)にたいして、$$\int_C \frac{1}{z - \alpha} dz = \begin{cases} 2 \pi j & (\alphaがCの内部にあるとき) \\ 0 & (\alphaがCの外部にあるとき) \end{cases}$$が成り立つ。
定理:積分と留数
\(D \subset \mathbb{C}\)を単連結領域、\(\alpha \in D \)とする。いま \(f : D - \{\alpha \} \to \mathbb{C}\)が正則であるとし、ローラン展開\(f(z) = \sum_{n \in \mathbb{Z}} a_n (z - \alpha)^n \)をもつとする。このとき、\(\alpha\)をその内部に含む\(D\)内の単純閉曲線\(C\)について、以下が成立する。$$\int_C f(z)dz = 2 \pi j \cdot a_{-1}$$または、$$\int_C f(z)dz = 2 \pi j \text{Res}(f(z),\; \alpha)$$
【証明】積分定理より、\(C = C(\alpha,\;r)\)(ただし、\(r\)は十分小さく、\(C \subset D\))としてよい。基本公式の2.により、\(n \neq -1\)のとき、\(\int_C (z - \alpha)^n = 0\)、\(n=-1\)のとき、\(\int_C (z - \alpha)^n = 2 \pi j\)である。よって、ローラン展開より、$$\int_C f(z) dz = \int_C \left(\sum_{n \in \mathbb{Z}} a_n(z - \alpha)^n \right)dz = \sum_{n \in \mathbb{Z}} \left(a_n \int_C (z - \alpha)^n dz \right) = 2\pi j \cdot a_{-1}$$となる。
この証明から分かるように、\(f(z)\)を極の周りでローラン展開してから積分すると、\(a_{-1}\)の項だけが残り(留まり)、それ以外の項は消えてしまう。この\(a_{-1}\)(\(z - \alpha)^{-1}\)の係数)を\(f\)の\(\alpha\)における留数とよび、\(\text{Res}(f(z),\;\alpha)\)と表す。
留数の具体例
1.\(\frac{e^z}{z^2}\)の\(z=0\)における留数を求める。
ローラン展開$$\frac{e^z}{z^2} = \frac{1}{z^2} + \frac{1}{z} + \frac{1}{2!} + \frac{z}{3!} + \cdots$$より、\(\text{Res}(e^z/z^2 , 0)=1\)となる。例えば、\(C = C(0,1)\)とすると、\(\int_C \frac{e^z}{z^2} dz = 2 \pi j \cdot 1 = 2 \pi j\)となる。
2.\(C = C(0,\;1)\)にたいし、\(\int_C \frac{1}{z^2(z-2)}dz\)を計算する。
\(D = \{|z|<2\}\)とすると被積分関数は\(D - \{0\}\)で正則であるから、$$\int_C \frac{1}{z^2(z-2)} dz = 2 \pi j \text{Res}\left(\frac{1}{z^2(z-2)},\;0\right)$$また、ローラン展開は$$\frac{1}{z^2(z-2)} = -\frac{1}{2z^2} - \frac{1}{4z} - \frac{1}{8} - \frac{z}{16}- \cdots$$なので$$\text{Res}\left(\frac{1}{z^2(z-2)},\;0\right) = -\frac{1}{4}$$である。よって、求める積分は、\(2\pi j \cdot \frac{-1}{4} = -\frac{\pi j}{2}\)である。
留数の計算公式
\(f(z) = \frac{g(z)}{(z - \alpha)^k}\)、\(g(z)\)は\(z=\alpha\)のまわりで正則なとき、$$\text{Res}(f(z),\;\alpha) =\frac{1}{2 \pi j}\int_C f(z)dz =\frac{1}{2 \pi j}\int_C \frac{g(z)}{(z - \alpha)^k}dz \\= \frac{1}{(k-1)!}g^{(k-1)}(\alpha)$$である。とくに\(k=1\)のとき、\(\text{Res}(f(z),\;\alpha) = g(\alpha)\)
留数定理
\(C\)を\(\mathbb{C}\)内の単純閉曲線、\(D\)をその内部とし、関数\(f\)は\(D - \{\alpha_1,\alpha_2,\cdots,\alpha_n\}\)において、正則であるとする。ただし、\(\{\alpha_1,\alpha_2,\cdots,\alpha_n\}\)は互いに異なる\(D\)内の点である。このとき、以下が成り立つ。$$\int_C f(z)dz = 2 \pi j\sum_{k=1}^n \text{Res}(f(z),\;\alpha_k)$$
【証明】
\(r>0\)を十分に小さくとり、\(C_k = C(\alpha_k,\;r)\)とすれば、\(C_1,C_2,\ldots,C_n\)はすべて\(D\)に含まれ、かつそれぞれ互いに交わらないとできる。コーシの積分定理より、$$\int_C = \int_{C_1}+\int_{C_2}+\cdots+\int_{C_n}$$なので、「定理:ローラン展開」より留数定理が成り立つ。
留数定理を使った積分計算
\(C=C(0,\;2)\)とし、\(I=\int_C \frac{e^{jz}}{z^2 +1}dz\)を計算する。
\(f(z) = \frac{e^{jz}}{z^2 +1}\)は、\(\mathbb{C}-\{\pm j\}\)で正則で、その極\(z=\pm j\)は、\(|z|=1\)で積分路\(C\)の半径\(R=2\)より小さいので、\(C\)の内部にある。留数定理より、積分\(I\)は積分路\(C\)の内部にあるすべての留数の和に\(2\pi j\)をかけたものに等しいので、$$I = \int_C f(z) dz = 2 \pi j \{\text{Res}(f(z),\; j) + \text{Res}(f(z) ,\; -j)\}$$である。特異点\(z_1=j, \;z_2=-j\)は、分母が\((z-j)(z+j)\)と因数分解できるため、いずれも1位の極(単純極)である。単純極における留数は、次の公式で計算できる。$$\text{Res}( f(z),\; z_k) = \lim_{z \to z_k} (z - z_k) f(z)$$・\(z_1 = j\)の留数は、$$\text{Res}(f(z), \; j) = \lim_{z \to j} (z - j) \frac{e^{jz}}{(z - j)(z + j)} = \lim_{z \to j} \frac{e^{jz}}{z + j}= \frac{e^{-1}}{2j}$$ である。
・\(z_2=-j\)の留数は、$$\text{Res}(f(z),\;-j) = \lim_{z \to -j} (z - (-j)) \frac{e^{jz}}{(z - j)(z + j)} = \lim_{z \to -j} \frac{e^{jz}}{z - j}= -\frac{e}{2j}$$である。よって、$$I = 2 \pi j \left(\frac{e^{-1}}{2j} - \frac{e}{2j}\right) = \pi(e^{-1} - e)$$

