37. コーシーの積分公式(複素関数)
コーシーの積分定理と同じ仮定の下で、コーシーの積分公式が成立する。
コーシーの積分公式
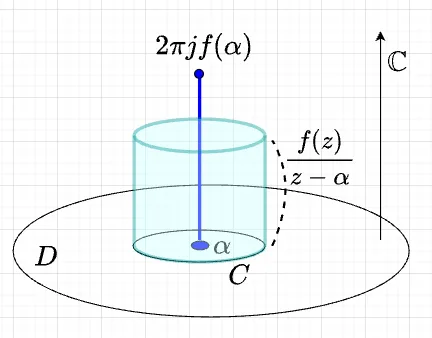
\(D\)を\(\mathbb{C}\)内の単連結領域とし、\(C\)を\(D\)内の単純閉曲線とする。関数\(f:D \to \mathbb{C}\)が正則であれば、任意の\(\alpha \in (Cの内部)\)にたいして、以下が成立する。$$f(\alpha) =\frac{1}{2 \pi j} \int_C \frac{f(z)}{z - \alpha} dz$$※ここで、\(C\)は反時計回りの向きを持つ閉曲線とする。
【証明(概要)】
証明したい積分を\(I\)とする。 $$I = \int_C \frac{f(z)}{z - \alpha} dz$$点\(\alpha\)は閉曲線\(C\)の内部にあり、被積分関数\(\frac{f(z)}{z - \alpha}\)は\(z = \alpha\)で特異点を持つため、コーシーの積分定理をそのまま適用することはできない。そこで、\(\alpha\)を中心とし、\(C\)の内部に含まれるように十分小さな半径 \(\rho\)の円周\(C_\rho\)を考える。\(C_\rho\)の向きも反時計回りとする。
ここで、関数\(g(z) = \frac{f(z)}{z - \alpha}\)は、領域\(R\)(\(C\)と \(C_\rho\)に囲まれた領域)において正則である。したがって、多重連結領域におけるコーシーの積分定理により、次の関係が成り立つ。$$\int_C \frac{f(z)}{z - \alpha} dz = \int_{C_\rho} \frac{f(z)}{z - \alpha} dz$$ここで、右辺の積分を\(I_\rho\)とおき、次の変形を行う。$$I_\rho = \int_{C_\rho} \frac{f(z)}{z - \alpha} dz = \int_{C_\rho} \frac{f(\alpha) + (f(z) - f(\alpha))}{z - \alpha} dz \\ = f(\alpha) \int_{C_\rho} \frac{1}{z - \alpha} dz + \int_{C_\rho} \frac{f(z) - f(\alpha)}{z - \alpha} dz = f(\alpha) J_1 + J_2$$
*\(J_1\):円 \(C_\rho\)は\(z = \alpha + \rho e^{j \theta}\) (\(0 \le \theta \le 2\pi\)) と媒介変数表示できる。$$z - \alpha = \rho e^{j\theta}, \quad dz = j \rho e^{i\theta} d\theta$$これを\(J_1\)に代入する。$$J_1 = \int_0^{2\pi} \frac{1}{\rho e^{j \theta}} (j \rho e^{j \theta} d\theta) = \int_0^{2\pi} j d\theta = 2\pi j$$
*\(J_2\):\(f(z)\)は\(\alpha\)で正則であるため、\(\alpha\)で連続である。従って、任意の\(\epsilon > 0\)に対して、\(|z - \alpha| < \delta\)ならば\(|f(z) - f(\alpha)| < \epsilon\)となる \(\delta\)が存在する。\(C_\rho\)の半径\(\rho\)をこの \(\delta\)より小さく \((\rho < \delta)\)選ぶと、曲線\(C_\rho\)上の任意の点\(z\)に対して\(|f(z) - f(\alpha)| < \epsilon\)が成り立つ。
ここで、\(J_2\)の絶対値を評価する。積分のML不等式(\(|\int_C g(z) dz| \le M L\)、\(M = \max|g(z)|\)、\(L = 曲線の長さ\))を使う。$$|J_2| = \left| \int_{C_\rho} \frac{f(z) - f(\alpha)}{z - \alpha} dz \right| \le \max_{z \in C_\rho} \left| \frac{f(z) - f(\alpha)}{z - \alpha} \right| \cdot (l(C_\rho))$$ \(C_\rho\)上では\(|z - \alpha| = \rho\) であり、\(|f(z) - f(\alpha)| < \epsilon\)である。また、円\(C_\rho\)の長さは\(2\pi\rho\)である。$$|J_2| \le \frac{\epsilon}{\rho} \cdot (2\pi\rho) = 2\pi\epsilon$$ \(\epsilon\)は任意の正の数であるため、\(\epsilon \to 0\)と極限をとることで、$$|J_2| = 0 \Rightarrow J_2 = 0$$となる。\(I_\rho = f(\alpha) J_1 + J_2\)に、求めた\(J_1 = 2\pi j\) と \(J_2 = 0\)を代入すると、$$I_\rho = f(\alpha) (2\pi j) + 0$$ $$\int_{C_\rho} \frac{f(z)}{z - \alpha} dz = 2\pi j f(\alpha)$$ \(\int_C \frac{f(z)}{z - \alpha} dz = \int_{C_\rho} \frac{f(z)}{z - \alpha} dz\) から、$$\int_C \frac{f(z)}{z - \alpha} dz = 2\pi j f(\alpha)$$よって、$$f(\alpha) = \frac{1}{2\pi j} \int_C \frac{f(z)}{z - \alpha} dz$$
コーシーの積分公式の応用
1)\(I_1 = \int_C \frac{z^2}{z - j} dz\)の積分値を求める。(\(C=C(0,2)\))
\(D = \mathbb{C}, \quad f(z) = z^2, \quad \alpha = j\)として、コーシーの積分公式を適用する。\(D\)は単連結領域であり、\(f\)は\(D\)上で正則。\(j \in (Cの内部)\)であるから、$$f(j) = \frac{1}{2 \pi j}\int_C \frac{z^2}{z - j} dz \Rightarrow I_1 = 2 \pi j f(j) = -2 \pi j$$となる。
2)\(I_2 = \int_C \frac{e^z}{z^2 -4 z +3} dz\)の積分値を求める。(\(C=C(0,2)\))
被積分関数は、\(\frac{e^z}{(z-1)(z-3)}\)と変形できる。特異点は\(z=1, \; 3\)となるが、\(C\)の内部にあるのは1だけである。そこで、\(f(z) = \frac{e^z}{z-3}, \quad \alpha=1\)としてコーシーの積分公式を適用する。\(D\)としては原点中心半径\(2.5\)の円板をとる。これは\(C\)をふくむ単連結領域であり、その上で\(f(z)\)は正則である。よって、$$f(1) = \frac{1}{2 \pi j}\int_C \frac{e^z}{(z-1)(z-3)} dz \Rightarrow I_2 = 2 \pi j f(1) = 2 \pi j \frac{e^1}{1 - 3} = - \pi e j$$となる。
微分可能性
コーシーの積分公式の拡張(高階導関数の公式)を考える。
高階導関数の公式
単連結領域\(D\)内で関数\(f(z)\)が正則であるとし、\(D\)内の単純閉曲線\(C\)と、その内部の任意の点\(\alpha\)を考える。このとき、\(f(z)\)は\(D\)上で何回でも微分可能であり、任意の非負整数 \(n\)に対して次の公式が成り立つ。$$f^{(n)}(\alpha) = \frac{n!}{2 \pi j} \int_C \frac{f(z)}{(z - \alpha)^{n+1}}dz$$
※この公式は、複素関数が一度正則であれば、それは無限回微分可能であるということを示している。実関数の場合には、一度微分可能であっても無限回微分可能であるとは限らない(例: \(f(x) = x|x|\)は \(x=0\)で1回微分可能だが2回微分可能ではない、\(f'(x)=2|x|\)だが、2回微分はできない)。この性質は、実解析にはない、複素解析特有の非常に強力な性質である。
【証明(概要)】(数学的帰納法による)
・\(n = 0\)の場合:$$f(\alpha) = \frac{1}{2 \pi j} \int_C \frac{f(z)}{z - \alpha}dz$$となり、コーシーの積分公式そのものとなる。
・\(n = k\)の場合:\(n = k\)のときに公式が成り立つと仮定する。$$f^{(k)}(\alpha) = \frac{k!}{2 \pi j} \int_C \frac{f(z)}{(z - \alpha)^{k+1}}dz \quad \cdots (1)$$
・\(n = k +1\)の場合:\(f^{(k+1)}(\alpha)\)は、導関数の定義により \(f^{(k)}(\alpha)\)を\(\alpha\)で微分した極限として表される。$$f^{(k+1)}(\alpha) = \lim_{h \to 0} \frac{f^{(k)}(\alpha + h) - f^{(k)}(\alpha)}{h}$$ここで、式(1)を用いて\(f^{(k)}(\alpha + h)\)を表すと、$$f^{(k)}(\alpha + h) = \frac{k!}{2 \pi j} \int_C \frac{f(z)}{(z - (\alpha + h))^{k+1}}dz$$となり、これらを\(f^{(k+1)}(\alpha)\) の定義式に代入する。$$f^{(k+1)}(\alpha) = \lim_{h \to 0} \frac{1}{h} \left[ \frac{k!}{2 \pi j} \int_C \frac{f(z)}{(z - \alpha - h)^{k+1}}dz - \frac{k!}{2 \pi j} \int_C \frac{f(z)}{(z - \alpha)^{k+1}}dz \right]$$積分の線形性により、項をまとめる。$$f^{(k+1)}(\alpha) = \frac{k!}{2 \pi j} \int_C f(z) \left[ \lim_{h \to 0} \frac{1}{h} \left( \frac{1}{(z - \alpha - h)^{k+1}} - \frac{1}{(z - \alpha)^{k+1}} \right) \right] dz \quad \cdots (2)$$【注】 \(\lim_{h \to 0}\)と \(\int_C\)の順序交換は、\(f(z)\)の正則性(有界性)と積分路\(C\)が閉曲線であることから許される。
角括弧内の極限部分は、関数\(g(\alpha) = \frac{1}{(z - \alpha)^{k+1}}\)の\(\alpha\)に関する導関数の定義そのものなので、$$\lim_{h \to 0} \frac{1}{h} \left( \frac{1}{(z - \alpha - h)^{k+1}} - \frac{1}{(z - \alpha)^{k+1}} \right) = \frac{d}{d\alpha} \left[ \frac{1}{(z - \alpha)^{k+1}} \right]$$なので、この微分を実行すると、$$\frac{d}{d\alpha} \left[ (z - \alpha)^{-(k+1)} \right] = -(k+1) (z - \alpha)^{-(k+1) - 1} \cdot (-1) \\ = (k+1) (z - \alpha)^{-(k+2)} = \frac{k+1}{(z - \alpha)^{k+2}}$$である。この結果を式(2)に代入すると、$$f^{(k+1)}(\alpha) = \frac{k!}{2 \pi j} \int_C f(z) \cdot \frac{k+1}{(z - \alpha)^{k+2}} dz \\ = \frac{(k+1)k!}{2 \pi j} \int_C \frac{f(z)}{(z - \alpha)^{k+2}} dz \\ =\frac{(k+1)!}{2 \pi j} \int_C \frac{f(z)}{(z - \alpha)^{(k+1)+1}} dz$$となり、これは\(n = k+1\)のときの公式に他ならない。従って、数学的帰納法により、任意の非負整数\(n\)に対して公式が成り立つことが証明された。
積分計算への応用
\(C = C(0,2)\)として、以下の積分値を求める。$$I = \int_C \frac{e^z}{(z - 1)^2} dz$$ \(D = \mathbb{C}, \quad f(z) = e^z, \quad \alpha =1, \quad n=1\)として、高階導関数の公式を適用する。\(1 \in (Cの内部)\)であるから、$$f'(1) = \frac{1}{2 \pi j} \int_C \frac{e^z}{(z-1)^2} \Rightarrow I = 2 \pi j f'(1) = 2 \pi j e$$となる。

