36. 積分定理の応用と証明(複素関数)
コーシーの積分定理
\(D\)を\(\mathbb{C}\)内の単連結領域とし、\(C\)を\(D\) 内の単純閉曲線とする。このとき、関数\(f : D \to \mathbb{C}\)が正則であれば、$$\int_C f(z) dz =0$$となる。
(積分路の変形)\(D\)を\(\mathbb{C}\)内の単連結領域とし、関数\(f : D \to \mathbb{C}\)は正則とする。このとき、任意の\(\alpha,\; \beta \in D\)および任意の\(\alpha\)から\(\beta\)への曲線\(C_1,\; C_2 \subset D\)にたいし、$$\int_{C_1} f(z) dz = \int_{C_2} f(z) dz $$が成立する。
基本公式
任意の単純閉曲線\(C\)にたいし、$$\int_C \frac{1}{z - \alpha} dz = \begin{cases} 2 \pi j & (\alpha が C の内部にあるとき)\\ 0 & (\alpha がCの外部にあるとき)\end{cases}$$が成り立つ。
※なお\(\alpha\)が\(C\)上にあるときは、積分自体が定義できない。
【証明(概要)】
・\(\alpha\)が\(C\)の外部にあるとき:関数\(f(z) = \frac{1}{z - \alpha}\)は、曲線\(C\)およびその内部を含む領域\(D\)で正則である。特異点\(\alpha\)が\(C\)の外部にあるため、領域\(D\)において\(f(z)\)は微分可能であり正則。コーシーの積分定理により、単純閉曲線\(C\)の内部全体で関数が正則であれば、その閉曲線に沿った線積分は\(0\)になる。$$\int_C f(z) dz = \int_C \frac{1}{z - \alpha} dz = 0 $$従って、\(\alpha\)が\(C\) の外部にあるとき、積分は\(0\)である。
・\(\alpha\)が\(C\)の内部にあるとき:特異点\(\alpha\)が\(C\)の内部にあるため、コーシーの積分定理を直接適用できないので、特異点\(\alpha\)を含む領域を積分路\(C\)から除外する手法(積分路の変形)を用いる。
\(\alpha\)を中心とし、かつ\(C\)の内部に完全に含まれるように十分に小さな円\(\Gamma\)を取る。このとき、曲線\(C\)と\(\Gamma\)で囲まれた領域\(D'\)において、関数\(f(z) = \frac{1}{z - \alpha}\)は正則となる。
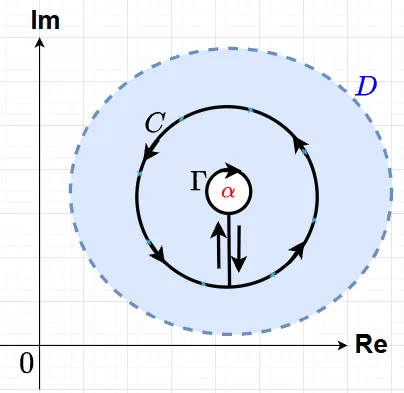
具体的には、\(C\)から\(\Gamma\)へと伸びる一本の直線(または曲線)\(L_1\)を引き、\(L_1\)に沿って戻る別の直線\(L_2\)を、逆方向に引く。この\(L_1\)と\(L_2\)を切断線と呼び、この切断線を設けることで、経路\(C \cup L_1 \cup (-\Gamma) \cup L_2\)は全体として一つの単純閉曲線となり、その内部全体で関数\(f(z)\)が正則になる。この正則な領域\(D'\)の境界に沿った積分(\(C\)を反時計回り、\(\Gamma\)を時計回りに一周した積分路 \(C' = C \cup (-\Gamma)\))は\(0\)になる。
$$\int_{C} \frac{1}{z - \alpha} dz + \int_{-\Gamma} \frac{1}{z - \alpha} dz = 0, \quad \int_{C} \frac{1}{z - \alpha} dz - \int_{\Gamma} \frac{1}{z - \alpha} dz = 0 \\ \int_{C} \frac{1}{z - \alpha} dz = \int_{\Gamma} \frac{1}{z - \alpha} dz$$また、切断線部分の積分は相殺される。これにより、元の積分は小さな円\(\Gamma\)上の積分に置き換えられる。
・円\(\Gamma\)上の積分の計算:円\(\Gamma\)のパラメータ表示を、中心\(\alpha\)、半径\(\rho\)、反時計回りとして、以下のように定義する\(z(t) = \alpha + \rho e^{jt} \quad (0 \le t \le 2\pi) \)
微分\(dz\)は、\(dz = j\rho e^{jt} dt\)なので、これらを積分に代入すると、$$\int_{\Gamma} \frac{1}{z - \alpha} dz = \int_0^{2\pi} \frac{1}{(\alpha + \rho e^{jt}) - \alpha} (j\rho e^{jt} dt) \\ = \int_0^{2\pi} \frac{1}{\rho e^{jt}} (j\rho e^{jt} dt) = \int_0^{2\pi} j dt = 2 \pi j$$となる。以上より、\(\alpha\)が\(C\)の内部にあるとき、積分は \(2\pi j\)となる。
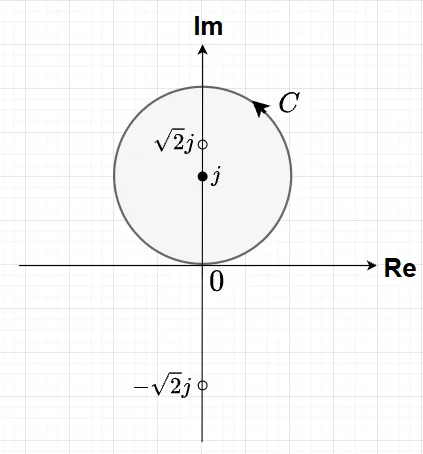
【基本公式の応用例】\(C = C(j,1)\)(左回り)として、\(\int_C \frac{1}{z^2 + 2} dz\)を求める。被積分関数を$$f(z) = \frac{1}{z^2+2} = \frac{1}{j 2\sqrt{2}}\left(\frac{1}{z - j \sqrt{2}} - \frac{1}{z + j \sqrt{2}}\right)$$と変形すると、$$\int_C \frac{1}{z^2 + 2} dz \\= \frac{1}{j 2 \sqrt{2}}\left(\int_C \frac{1}{z - j \sqrt{2}} dz - \int_C \frac{1}{z + j \sqrt{2}} dz \right)$$となる。ここで、\(j \sqrt{2}\)は\(C\)の内部、\( - j \sqrt{2}\)は\(C\)の外部にあるので、基本公式より求める積分は$$\frac{1}{j 2 \sqrt{2}}(2 \pi j - 0)= \frac{\pi}{\sqrt{2}}$$となる。
グリーンの定理
\(C\)を\(R^2\)内の単純閉曲線とし、その内部を\(R\)と表す。関数\(P(x,\; y)\)と\(Q(x, \; y)\) が\(C \cup R\)を含む開集合上で\(C^1\)級であるとき、$$\int_C (P dx + Q dy) = \iint_R \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right) dx dy$$が成り立つ。
すなわち、\(P(x,\; y)\)と\(Q(x, \; y)\) の\(C\)上の線積分が、その外微分の領域\(R\)上の重積分に一致する。
※グリーンの定理の証明は、グリーンの定理(高校数学の美しい物語)を参考にしてください。
コーシーの積分定理の証明
複素関数\(f(z)\)は、実部\(u(x, y)\)と虚部\(v(x, y)\)を用いて次のように表される。$$f(z) = u(x, y) + j v(x, y)$$ここで、\(z = x + j y\)であり、\(x , \;y\)は実数。また、線積分\(\int_C f(z) dz\)を実数の積分に分解する。\(dz = d(x + j y) = dx + j dy\)なので、$$\int_C f(z) dz = \int_C (u + j v)(dx + j dy) \\= \int_C (u dx - v dy) + j \int_C (v dx + u dy)$$分解した積分の実部と虚部にそれぞれグリーンの定理を適用する。
・実部:\(P = u, Q = -v\)としてグリーンの定理を適用する。$$\int_C (u dx - v dy) = \iint_R \left(\frac{\partial (-v)}{\partial x} - \frac{\partial u}{\partial y}\right) dx dy \\ = \iint_R \left(-\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right) dx dy \quad \cdots (1)$$ ・虚部:\(P = v, Q = u\)としてグリーンの定理を適用する。$$\int_C (v dx + u dy) = \iint_R \left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) dx dy \quad \cdots (2)$$ \(f(z)\)は領域\(D\)(したがって\(R\))で正則であると仮定している。関数\(f(z)\)が正則であるための必要十分条件は、実部\(u\)と虚部\(v\)がコーシー・リーマンの関係式を満たすことである。$$\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} , \quad \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$$この関係式を、グリーンの定理を適用した結果を式(1)と式(2)に代入する。
・式(1):$$\iint_R \left(-\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right) dx dy$$ここで、コーシー・リーマンの関係式\(\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}\)を用いると、$$= \iint_R \left(\frac{\partial u}{\partial y} - \frac{\partial u}{\partial y}\right) dx dy = 0$$
・式(2):$$\iint_R \left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) dx dy$$ここで、コーシー・リーマンの関係式\(\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}\)を用いると、$$= \iint_R \left(\frac{\partial u}{\partial x} - \frac{\partial u}{\partial x}\right) dx dy = 0$$従って、線積分 \(\int_C f(z) dz\)の実部と虚部はともに0となり、$$\int_C f(z) dz = 0 + j \cdot 0 = 0$$である。

