35. コーシーの積分定理(複素関数)
まず、複素線積分を計算可能な積分に置き換えることを考える。
複素線積分の計算公式
\(D \subset \mathbb{C}\)とし、\(f:D \to \mathbb{C}\)を連続関数とする。このとき、滑らかな曲線\(C: z=z(t)=x(t)+j y(t) \quad (a \leq t \leq b)\)に沿った複素線積分は、$$\int_C f(z)dz = \int_a^b f(z(t))\cdot z'(t) dt $$で与えられる。ただし、\(z'(t) = \frac{d}{dt}z(t)\)とする。
複素関数\(f(z)\)および曲線\(C\)上の微小変位\(dz\)を、実部と虚部に分解する。 ここで、\(z = x + j y\)とする。\(f(z) = u(x, y) + j v(x, y)\) (\(u,\;v\)は実数関数) また、 曲線 \(C\)上の微小変位\(dz\)は、\(dz = dx + j dy\)である。
複素線積分\(\int_C f(z) dz\)は、リーマン和の極限として、次のように定義される。
$$\int_C f(z) dz = \lim_{|\Delta z_k| \to 0} \sum_{k=1}^n f(\zeta_k) \Delta z_k $$ここで、 \(\Delta z_k = \Delta x_k + j \Delta y_k\) 。 被積分項 \(f(z) dz\)を展開すると、$$f(z) dz = (u + j v)(dx + j dy) \\ = (u dx + j u dy + j v dx + j^2 v dy) \\ = (u dx - v dy) + j (v dx + u dy) $$従って、複素線積分の定義は、2つの実数線積分の和として表される。$$\int_C f(z) dz = \int_C (u dx - v dy) + j \int_C (v dx + u dy) \quad \cdots (1)$$式 (1) の右辺にある2つの実数線積分を、曲線\(C\)のパラメータ表示\(z(t) = x(t) + j y(t)\)を使って\(t\)の積分に変換する。 曲線 \(C\)が\(z(t) = x(t) + j y(t) \quad (a \leq t \leq b)\) で与えられるとき、 \(dx = x'(t) dt \quad \text{および} \quad dy = y'(t) dt\)よって、$$\int_C (u dx - v dy) = \int_a^b \left[ u(x(t), y(t)) \frac{dx}{dt} - v(x(t), y(t)) \frac{dy}{dt} \right] dt \quad \cdots (2)$$また、$$\int_C (v dx + u dy) = \int_a^b \left[ v(x(t), y(t)) \frac{dx}{dt} + u(x(t), y(t)) \frac{dy}{dt} \right] dt \quad \cdots (3)$$となる。
式 (1) に式 (2) と (3) を代入し、結合する。$$\int_C f(z) dz = \int_a^b \left[ u \frac{dx}{dt} - v \frac{dy}{dt} \right] dt + j \int_a^b \left[ v \frac{dx}{dt} + u \frac{dy}{dt} \right] dt $$両者を一つの\(t\)の積分にまとめる。 $$\int_C f(z) dz = \int_a^b \left[ \left( u \frac{dx}{dt} - v \frac{dy}{dt} \right) + j \left( v \frac{dx}{dt} + u \frac{dy}{dt} \right) \right] dt $$ここで、被積分関数の中身を展開して整理する。 $$\left( u \frac{dx}{dt} + j u \frac{dy}{dt} \right) + \left( j v \frac{dx}{dt} + j^2 v \frac{dy}{dt} \right) \\ = u \left( \frac{dx}{dt} + j \frac{dy}{dt} \right) + j v \left( \frac{dx}{dt} + j \frac{dy}{dt} \right)$$ここで、曲線\(z(t)\)の微分\(z'(t)\)は、$$z'(t) = \frac{dz}{dt} = \frac{dx}{dt} + j \frac{dy}{dt}$$これを利用して、共通因子\(\left( \frac{dx}{dt} + j \frac{dy}{dt} \right)\)でくくると、$$= (u + j v) \left( \frac{dx}{dt} + j \frac{dy}{dt} \right) \\ = f(z(t)) \cdot z'(t) $$従って、求める複素線積分の定義式が得られる。 $$\int_C f(z) dz = \int_a^b f(z(t)) \cdot z'(t) dt $$
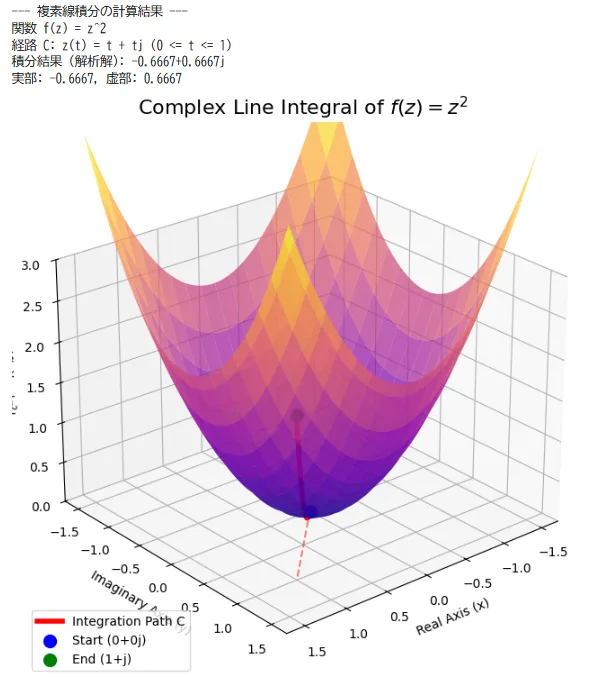
【具体例1】関数を\(f(z) = z^2\) として、曲線\(C : z = z(t) = t + j t \quad (0 \leq t \leq 1)\) に沿った複素線積分を計算する。
複素線積分は、次の式で計算される。$$\int_C f(z) dz = \int_a^b f(z(t)) z'(t) dt$$ 複素関数と経路は、\(f(z)=z^2,\quad z(t) = t + j t =t(1+j)\) $$z'(t) = \frac{dz}{dt} = 1 + j \\ f(z(t)) = (t + j t)^2 = (t(1+j))^2 = t^2 (1+j)^2 = t^2 (1 + 2j - 1) = 2j t^2 \\ \int_C f(z) dz = \int_0^1 (2j t^2) (1 + j) dt \\ = \int_0^1 (2j + 2j^2) t^2 dt = \int_0^1 (2j - 2) t^2 dt \\ = (2j - 2) \int_0^1 t^2 dt = (2j - 2) \left[ \frac{t^3}{3} \right]_0^1 \\ = (2j - 2) \left( \frac{1}{3} - 0 \right) = \frac{-2+2j}{3}$$
図1は、積分経路とその経路上の関数 \(|f(z)|\)の値を視覚化したものである。曲面は複素関数 \(f(z) = z^2\)の絶対値\(|f(z)| = |z|^2 = x^2 + y^2\)を示す。これは、原点から離れるほど大きくなる放物面の形状となる。底面(複素平面)は、 赤い破線が、原点 (0, 0) から (1, 1)までを結ぶ直線経路\(C: y=x\)を示している。曲面上の赤い太線は、この経路 \(C\)に沿った関数\(|f(z)|\)の高さを示す。この図は、積分が複素平面上の経路(底面)と、その経路上の関数の値(曲面上の線)を考慮しながら行われることを示している。積分の最終的な結果は、表示されている絶対値ではなく、関数の実部と虚部、および微小変位\(dz\)の方向をすべて含んだ複素数値 \((-2+2j)/3\) となる。
【具体例2】複素数\(\alpha\)を中心とする半径\(r > 0\)の円を$$C(\alpha, r) :=\left\{z(t) = \alpha + re^{j t} \quad | 0 \leq t \leq 2\pi \right\}$$によって定める。向きは反時計回り(左回り、\(t\)の増加方向)である。このとき、以下が成り立つ。
\(m \in \mathbb{Z}, \quad C=C(\alpha,\;r)\)とするとき、\(r > 0\)の値によらず$$\int_C (z - \alpha)^m dz =\begin{cases} 0 & (m \neq -1) \\ 2\pi j & (m = -1) \end{cases}$$
\(z(t) = \alpha + re^{jt}\)より、\(z'(t)=jre^{jt}\)よって、$$\int_C (z - \alpha)^m dz = \int_0^{2\pi} (re^{jt})^m \cdot (jre^{jt}) dt = jr^{m+1} \int_0^{2\pi} e^{j(m+1)t} dt \\ = \begin{cases} jr^{m+1} \left[\frac{1}{(m+1)j} e^{j(m+1)t}\right]_0^{2\pi} & = 0 & (m \neq -1) \\ j\int_0^{2\pi} 1 \cdot dt & =2\pi j & (m=-1) \end{cases}$$
複素積分の基本性質
積分経路の曲線について以下の記号を導入する。
・\(C_1,\quad C_2\)を滑らかな曲線とするとき、\(C_1\)に沿って進んだ後、さらに\(C_2\)に沿って進む経路を\(C_1 + C_2\)で表す。
・曲線\(C\)が区分的に滑らかであるとは、\(C\)が有限個の滑らかな曲線\(C_1,C_2,\ldots,C_N\)を順に繋ぎ合わせたものになっているときをいい、\(C=C_1 + C_2 + \cdots +C_N\)と表す。
・区分的に滑らかな曲線\(C\)にたいし、これを逆に進む曲線を\(-C\)と表す。
複素積分の性質
\(f,\;g\)が曲線\(C\)上で連続な複素関数であるとき、次が成り立つ。
(1) \(\alpha,\;\beta \in \mathbb{C}\)にたいし、$$\int_C (\alpha f(z) + \beta g(z))dz = \alpha \int_C f(z) dz + \beta \int_C g(z) dz$$
(2) \(C= C_1 + C_2\)のとき、$$\int_C f(z) dz = \int_{C_1} f(z) dz + \int_{C_2} f(z) dz$$
(3) $$\int_C f(z) dz = - \int_{-C} f(z) dz$$
(4) \(l(C)\)を\(C\)の長さ、\(C\)上で\(|f(z)| \leq M\)のとき、$$\left|\int_C f(z) dz \right| \leq Ml(C)$$
【(4)の証明(概略)】\(C\)の任意の分割\(\Delta =\{z_k\}\)とその中間の点\(\{\zeta_k\}\)にたいし、そのリーマン和の絶対値について$$\left|\sum(f,\; \Delta)\right| = \left|\sum_k f(\zeta_k)(z_k - z_{k-1})\right| \leq \sum_k |f(\zeta_k)||z_k - z_{k-1}| \\ \leq M \sum_k |z_k - z_{k-1}| \leq M l(C)$$が成り立つ。この評価式はすべての分割について成立するので、\(\delta(\Delta) \to 0\)とした極限をとることで(4) を得る。ここで、最初の不等号は三角不等式を用いており、また右端の不等号は分割により\(C\)を折れ線近似した長さと\(C\) の長さを比較したものとなっている。
※厳密な証明とはなっていないことに注意。
コーシーの積分定理
コーシーの積分定理
\(D\)を\(\mathbb{C}\)内の単連結領域とし、\(C\)を\(D\)内の単純閉曲線とする。このとき、関数\(f:\;D \to \mathbb{C}\)が正則であれば、$$\int_C f(z) dz = 0$$である。
・曲線\(C\)が閉曲線であるとは、始点と終点が一致することをいう。\(C: z=z(t)\;\;(a \leq t \leq b)\)のとき、\(z(a) = z(b)\)
・単純閉曲線とは、\(C\)が自己交差しない閉曲線で、\(C:z=z(t)\;\;(a \leq t \leq b)\)のとき、\(a < t_1 <t_2<b \Longrightarrow z(t_1) \neq z(t_2) \)が成り立つことをいう。
・\(\mathbb{C}\)内の部分集合\(D\)が領域であるとは、「ひとつながり」の開集合であることをいう。
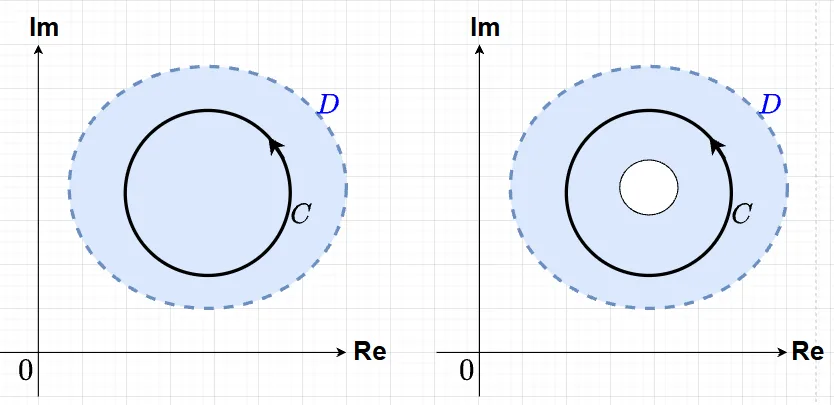
・\(\mathbb{C}\)上に単純閉曲線\(C\)が与えられたとき、\(\mathbb{C}-C\)はふたつの領域からなる(「Jordanの曲線定理」)。そのうち有界なほうを\(C\)の内部とよび、有界でないほうを\(C\)の外部とよぶ。
・領域\(D \subset \mathbb{C}\)が単連結であるとは、\(D\)内の任意の単純閉曲線\(C\)について、その内部が\(D\)に含まれることをいう。つまり、\(D\)に穴があいてないことをいう。
図2(左)は単連結の例で、領域\(D \subset \mathbb{C}\)において、\(D\) 内の任意の単純閉曲線\(C\)の内部が\(D\)に含まれている。一方、図2(右)では、単純閉曲線\(C\)の内部に穴があいているため、単連結ではない。
積分路の変形
\(D\)を\(C\)内の単連結領域とし、関数\(f : D \to \mathbb{C}\) は正則とする。このとき、任意の\(\alpha, \; \beta \in D\)および任意の\(\alpha\)から\(\beta\)への曲線\(C_1, \; C_2 \subset D\) にたいし、$$\int_{C_1} f(z) dz = \int_{C_2} f(z) dz$$である。
これは、「単連結領域上の正則関数の線積分は端点だけで値が決定される(経路独立性)」、もしくは「端点さえ固定していれば積分路は自由に変形してよい」ことを意味している。
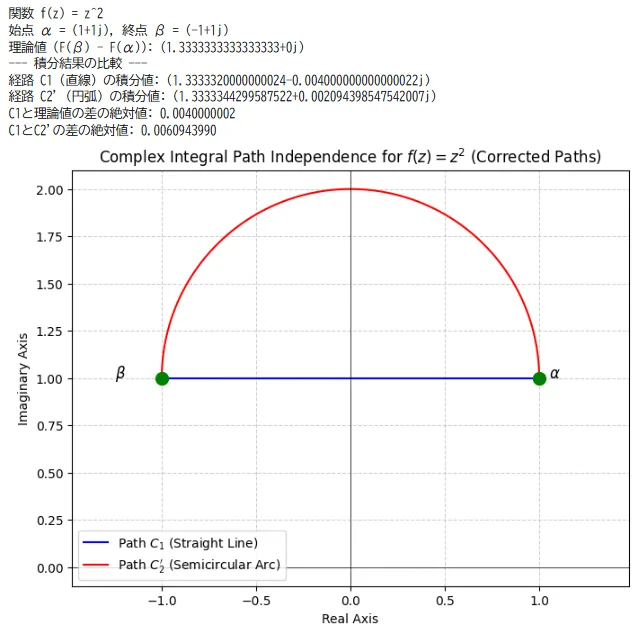
経路上での積分が等しくなるという性質を具体的に図3に示す。図3では、以下の設定で経路独立性を検証し、その経路例を図示する。
・正則関数\(f(z) = z^2\)(全複素平面で正則)
・始点\(\alpha=1 + j\)
・終点\(\beta=-1 + j\)
・経路\(C_1\)(直線経路)は、 \(\alpha\)から\(\beta\)への直線。
・経路\(C_2\)(放物線経路)は、実部が\(1\) から\(-1\)まで変化し、虚部は \(y(x) = \sqrt{1 - x^2} + 1\) となるような、上半円の経路。
理論的には、\(f(z) = z^2\)は、原始関数\(F(z) = \frac{1}{3}z^3\)を持つため、積分の値は経路によらず始点と終点の値のみで決まる。$$\int_{C} f(z) dz = F(\beta) - F(\alpha) = \frac{1}{3}\beta^3 - \frac{1}{3}\alpha^3=\frac{4}{3} \simeq 1.3333\ldots$$となる。
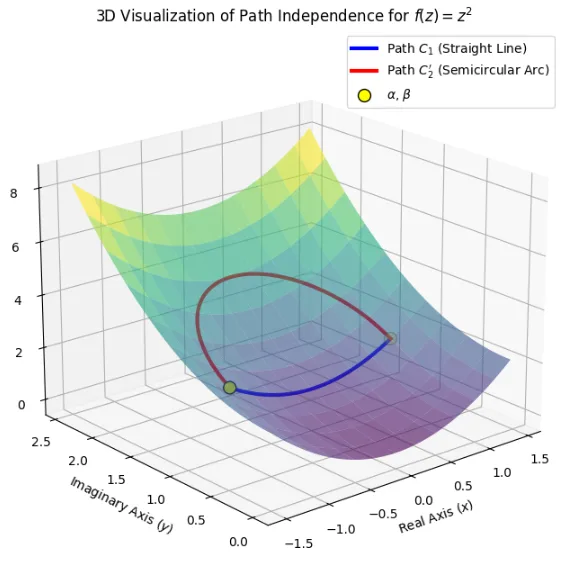
図4は、経路\(C_1\)(直線) と\(C_2\) (円弧) が通過する関数\(f(z) = z^2\)の絶対値\(|f(z)|\)の曲面上に、経路自体をプロットしている。
図3に示す積分値の数値計算結果でも、経路によらずほぼ同一の積分値が得られており、コーシーの積分定理の重要な性質を示している。

