34. 複素線積分(複素関数)
複素線積分においてコーシー・リーマンの定理が重要である。コーシー・リーマンの定理は、関数が正則(複素微分可能)であるための必要十分条件を与え、複素関数論の主要な成果は、この「正則性」という性質に大きく依存する。
コーシー・リーマン(CR)の定理と応用
領域\(D\)(\(D \subset \mathbb{C}\))上で定義された複素関数\(f(z) = u(x, y) + j v(x, y)\)が領域\(D\)上で正則(複素微分可能)であるための必要十分条件は、次の2つが満たされることである。
1)\(u(x, y)\) と\(v(x, y)\)が\(D\)上で偏微分可能であり、かつ偏導関数が連続である(\(f(z)\)が\(C^1\)級である)。
2)以下のコーシー・リーマンの方程式(CR方程式)が\(D\)上で成立する。$$\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \quad \text{and} \quad \frac{\partial v}{\partial x} = -\frac{\partial u}{\partial y}$$
【応用例】\(f(x+ j y) = u+j v\)が正則関数であり、かつ実部\(u = u(x, y)\) が\(u = y^3 - 3x^2 y\)をみたすとき,\(v = v(x,y)\) を定めることを考える。
CR方程式より、$$\frac{\partial u}{\partial x} = -6xy = \frac{\partial v}{\partial y} \cdots (1) \\ \frac{\partial u}{\partial y} = 3y^2 - 3x^2 = - \frac{\partial v}{\partial x} \cdots (2)$$が成り立つ。式(1)において\(v\)を\(y\)で積分すると、\(v = - 3xy^2 + g(x)\)(\(g(x)\)は\(x\)だけの関数)の形となる。これを\(x\)で偏微分すると、$$\frac{\partial v}{\partial x} = -3y^2 + \frac{d g(x)}{dx}$$となるので、式(2)と比較することで、\(\frac{d g(x)}{dx} = 3x^2\)を得る。よって\(g(x) = x^3 +C\)(\(C\)は実数の定数)。以上より、求める\(v\)は、$$v = -3xy^2 + x^3 + C \quad (C\in \mathbb{R})$$の形であることが必要となる。
十分性については、逆に\(v\)がこの形のとき、\(u,\;v\)は\(C^1\)関数であり、CR方程式も満たす。よって、\(f\)は正則である。
リーマン積分(実関数の積分)
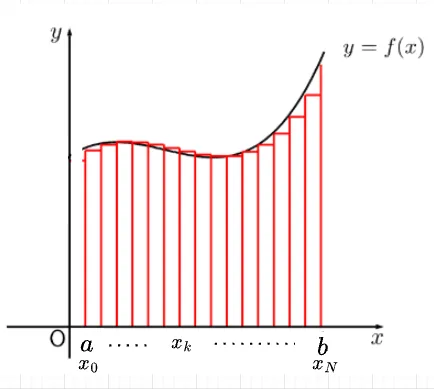
\(y = f(x)\) を区間\([a, \; b]\) で定義された連続関数とする。このとき、積分\(\int_a^b f(x) dx\)とは「\(y = f(x)\)と\(y = 0\)で囲まれる部分の(符号つき)面積」である。それは、図1のように「短冊」で近似した面積和の短冊を細くしていった極限値である。具体的には、区間\([a, \; b]\) に分割点\(a = x_0 < x_1 < \cdots < x_N = b\) をとるとき、有限和$$\sum_{k=0}^N f(x_k)(x_{k+1} - x_k)$$は短冊の面積の総和で、積分の近似値を与える。さらに\(N \to \infty\)として\(|x_{k+1} - x_k|\)の最大値を0に近づけると、それが積分値に収束する。
複素線積分
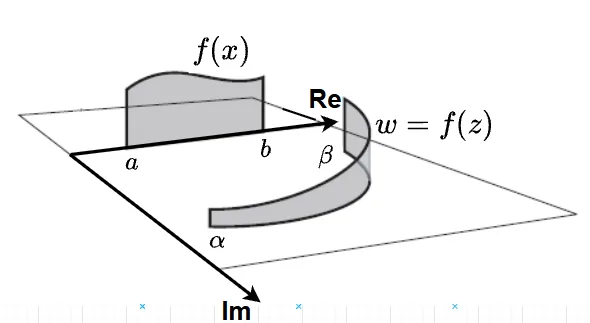
実関数のリーマン積分を複素数に拡張して考える。図2に示す概念図を基に考える。実数から複素数に世界が広がった分、積分の「経路」にもかなり自由度が生じる。例えば、図2に示す実関数\(f(x)\)の線積分の場合は、実数\(a\)から\(b\)へ進む経路は実軸上に制限されるので一意に定まる。
これに対して、複素関数\(f(z)\)の線積分の場合は、複素数\(\alpha \)から\(\beta \)を結ぶあらゆる曲線に沿った経路における積分を考えることになる。図2は、\(\alpha\)から\(\beta\)を結ぶ一つの曲線とそれに対応する\(w\)と線積分をイメージしている。
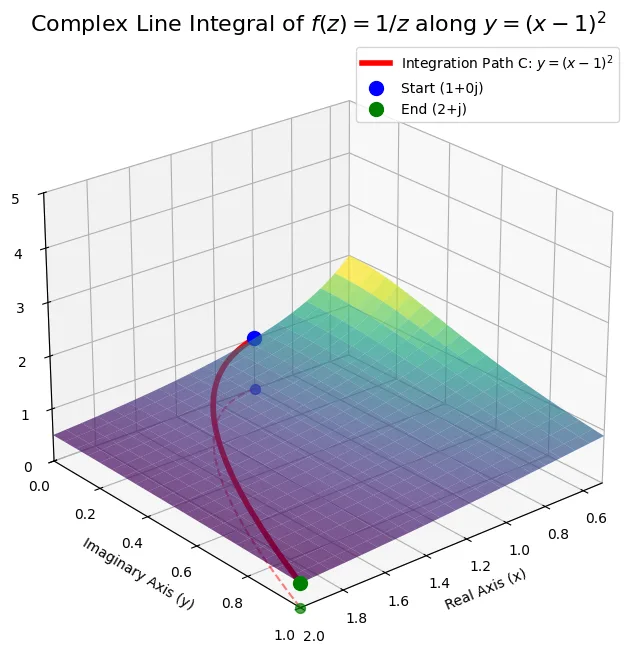
複素関数\(f(z)=1/z\)の線積分の具体的な例を図3に示す。底面(\(X-Y\) 平面)は複素平面で、赤い破線はその平面上にある一つの積分経路 \(y=(x-1)^2\)を示す。青い点は始点\(1+0j\)、緑の点は終点\(2+j\)である。曲面は、\(f(z) = 1/z\)の絶対値\(|f(z)| = 1/|z|\) を示す。原点\(z=0\)に近づくほど値が大きくなる(曲面が立ち上がる)様子が見られる。曲面上の赤い太線は、積分経路\(C\)に沿った関数\(|f(z)|\)の値を示している。積分は、この線の下にある「複雑な重み」をパスに沿って足し合わせるイメージとなる(結果は複素数である)。この図は、特定の二次曲線経路に沿った複素関数\(f(z)=1/z\)の振る舞いを示しており、積分経路の区間は原点\(z=0\)を含んでいないため、\(f(z)\)は経路上で正則である。
以下、複素線積分の概要をまとめる。\(D \subset \mathbb{C}\) とし、\(f : D \to \mathbb{C}\)を連続な関数とする。\(D\)内に曲線\(C\)とその分割\(\Delta := \left\{z_k = z(t_k)\right\}_{k=0}^N\)が与えられているとする。このとき、関数\(f\)の分割\(\Delta\)に関するリーマン和\(\sum (f,\; \Delta)\)を$$ \sum(f,\; \Delta) := \sum_{k=1}^N f(\zeta_k)\cdot (z_k - z_{k-1})$$によって定義する。ただし、\(\zeta_k\)は各\(k\)にたいし\(t_{k-1} \leq s_k \leq t_k\) となる\(s_k\)を自由に選び\(\zeta_k := z(s_k)\) として定まる\(C\)上の点とする。積\(f(\zeta_k)\cdot (z_k - z_{k-1})\)は実積分における「短冊の面積」に近い概念として対応する。
いま、ある複素数\(I\)が存在して、分割幅の最大値\(\max_{0 \leq k \leq N-1} |z_{k+1} - z_k|\)さえ十分に小さければ、「代表点」\(\left\{\zeta_1,\zeta_2,\ldots,\zeta_N\right\}\)の取り方によらず\(| I - \sum(f,\Delta)|\)がいくらでも0 に近い値となるとき、この複素数\(I\)を$$\int_C f(z) dz$$と表し、関数\(f\)の曲線\(C\)に沿った線積分という。
これは実関数の線積分の拡張になっている。これは、\(C\)が\(z(t)=t\;(t \in [a,b])\)と表され、\(f:[a,b] \to \mathbb{R}\)であれば、$$\int_C f(z)dz = \int_a^b f(t) dt \in \mathbb{R}$$となることからいえる。

