26．複素数と複素平面（複素関数）

注意：数学では虚数単位に\(i\)を用いることが多いが、ここでは、虚数単位として工学系で良く用いられる\(j\)を使う。

複素数

複素数 \(z=a+jb\)において、
・実部 (real part)：\(a\) のことを指し、\(Re(z)\) と表記される。
・虚部 (imaginary part)：\(b\) のことを指し、\(Im(z)\) と表記される。

\(\mathbb{C}\)の四則計算は以下のように定義する。
\(z = a + jb , \;\; w = c + jd \in \mathbb{C} \)とするとき、
１）\(a +j b = 0 \Longleftrightarrow 　a = b = 0 \Longleftrightarrow　(a^2 + b^2 = 0) \)
２）\(z \pm w = (a \pm c) + j(b \pm d)\)
３）\(zw = (ac - bd) + j(ad + bc)\)
４）\(w \neq 0\) のとき，$$ \frac{z}{w}= \frac{ac + bd}{c^2 + d^2} + j \frac{bc-ad}{c^2 + d^2}$$

\(z = a + jb\)にたいし、複素数\(a- jb\)を\(z\)の共役複素数（complex conjugate of z） とよび、\(\overline{z}\)で表す。これにより、以下の公式が成り立つ。

\(z = a + jb , \;\; w = c + jd \in \mathbb{C} \)とするとき、
１）\(\overline{(\overline{z})} = z \quad \quad\) ２） \(\overline{z + w} = \overline{z} + \overline{w} \quad \quad \) ３）\(\overline{z w} = \overline{z} \;\; \overline{w}\)
４）\(\overline{(\frac{z}{w})} = \frac{\overline{z}}{\overline{w}} \quad \quad \) ５）\(Re \{z\} = \frac{z + \overline{z}}{2} \quad \quad \) 　６） \(Im \{z\} = \frac{z - \overline{z}}{2j}\)
７）\(z \overline{z} = a^2 + b^2 (\geq 0)\)

複素平面（ガウス平面）

複素数\(z=a+jb\) を平面上の点\((a,b)\) に対応させて、複素数を幾何学的に表現するための座標平面のことを複素平面という。ガウス平面とも呼ばれる。複素平面を導入することで、複素数の計算が、点の移動や回転といった図形的な操作として解釈できるようになる。

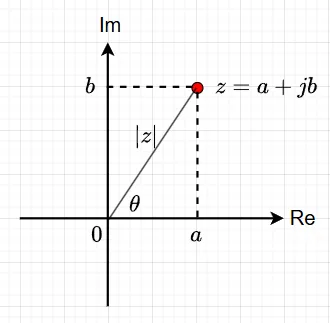
複素数の絶対値と偏角（極形式）

複素平面上の点は、直交座標 \((a,b)\) だけでなく、極座標\((r,θ)\) を用いて表すこともでき、この形式を極形式という。
1. 絶対値 (\(r\))
・原点 O から複素数\(z\)を表す点までの距離\(r\)のこと。複素数の絶対値\(∣z∣\) で表され、三平方の定理より\(∣z∣=r= \sqrt{a^2+b^2}= \sqrt{z \overline{z}}\)である。また、\(a = r \cos \theta ,\quad b = r \sin \theta\)である。
2. 偏角 (\(\theta\))
・実軸の正の向き（右側）から、原点 O と点\(z\)を結ぶ線分（動径）までに測った角度\(\theta\) のこと。\(\arg\; z\) と表記され、通常 \(0≤ \theta <2\pi\) または \(−\pi < \theta ≤ \pi\) の範囲で考える。

極形式

絶対値\(r\) と偏角\(\theta\)を用いて、複素数\(z\)は次のように表される。$$z = r(\cos \theta + j \sin \theta)$$さらに、オイラーの公式を使うと$$z = r e^{j \theta}$$ である。
この極形式を用いることで、複素数の乗算や除算が、回転と拡大・縮小という幾何学的な意味を持つことが明確になる。
・乗算：複素数どうしの積は、絶対値は掛け算され、偏角は足し算される（回転と拡大）。
・除算：複素数どうしの商は、絶対値は割り算され、偏角は引き算される（逆回転と縮小）。
\(z = r_1(\cos\theta_1 + j \sin \theta_1) , \;\; w = r_2(\cos\theta_2 + j \sin \theta_2) \in \mathbb{C} \)とするとき、$$z \; w = r_1 r_2 (\cos\theta_1 + j \sin \theta_1)(\cos\theta_2 + j \sin \theta_2) \\ = r_1 r_2 \{(\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2) + j(\sin \theta_1 \cos \theta_2 + \cos \theta_1 \sin \theta_2)\} \\= r_1 r_2 \{\cos(\theta_1 + \theta_2) + j \sin(\theta_1 + \theta_2)\} \\ = r_1 r_2 e^{j(\theta_1 + \theta_2)}$$となる。すなわち、複素数どうしの積は、絶対値は掛け算され、偏角は足し算される。まとめると、以下の公式となる。

複素数\(z,\; w \neq 0\)にたいして、
１）\(|z\; w|=|z|\;|w|\)かつ　\(\arg (z\;w) = \arg z + \arg w\)
２）\(|\frac{z}{w}| = \frac{|z|}{|w|}\)かつ　\(\arg (\frac{z}{w}) = \arg z - \arg w\)