9. 切換超平面の設計(3)
周波数整形による切換超平面の設計法
スライディングモード制御(SMC: Sliding Mode Control)は、システムのパラメータ変動や外乱に対して高いロバスト性(頑健性)を持つ非線形制御手法で、この制御法では、「切換超平面」と呼ばれる状態空間内の部分空間を設計し、システムの状態量をこの超平面上に拘束するように制御入力を切り換える。状態量が超平面上に拘束された状態が「スライディングモード」で、このモードではシステムの動的振る舞いは、切換超平面の設計のみに依存し、外乱やパラメータ変動の影響を受けにくくなる。しかし、通常、スライディングモード制御では、制御入力が不連続に切り替わるため、「チャタリング」と呼ばれる高周波振動が発生しやすいという問題がある。このチャタリングはアクチュエータの摩耗やシステムの高周波成分の励振を引き起こす可能性がある。切換超平面の周波数整形による設計法は、スライディングモード中のシステムの応答特性や、チャタリングの特性を周波数領域で考慮して切換超平面を設計するアプローチで、これによりシステムの安定性やロバスト性を維持しつつ、追従性能の向上、特定周波数帯の外乱抑制、チャタリングの低減などを目指す。
\(n\)次元の状態ベクトルを\(x \in R^n\) とするとき、切換超平面は一般に次のように定義される。\(\sigma(x,t) = 0\)ここで、\(\sigma\) はスカラー量である。スライディングモード制御の目的は、状態量\(x\)を有限時間内に\(\sigma (x,t)=0\)上に到達させ、その後、\(\sigma(x,t) = 0\)上に拘束し続けることである。状態量が\(\sigma(x,t)=0\)上に完全に拘束されている理想的なスライディングモードでは、\(\sigma(x,t)=0\)かつ
\(\dot \sigma(x,t)=0\)が成立する。この条件からシステムの動的振る舞いが導かれ、これが理想スライディングモードの動特性となる。この動特性は、元のシステムのパラメータや外乱に依存せず、切換超平面の設計パラメータのみによって決定される。
切換超平面の周波数整形では、この理想スライディングモードの動的振る舞いが望ましい周波数特性を持つように切換超平面を設計する。主な目的は以下となる。
・偏差の周波数特性の改善:指令値追従制御の場合、偏差 \(e\)(目標値と実測値の差)に関する動特性を設計する。例えば、低周波域での追従ゲインを高くして定常偏差を小さくしたり、特定の周波数帯域でのピークゲインを抑えて振動的な応答を抑制したりする。
・外乱抑制特性の向上:特定の周波数帯に存在する外乱の影響を低減するように、外乱から出力(または偏差)への伝達特性を整形する。
・チャタリングの低減:切換超平面の設計や、制御入力の連続化(境界層の導入など)と併せて、チャタリングの周波数成分を考慮することがある。
PID型切換超平面
一般的なアプローチの一つとして、偏差\(e(t)\)とその微分\(\dot e(t)\)、積分\(\int e(\tau) d \tau\)を用いて切換関数を設計する方法がある。これは、PID制御の考え方を切換超平面の設計に取り入れたものと解釈できる。 例えば、2階のシステムで偏差 \(e = y_d - y\)(\(y_d\): 指令値、 \(y\): 実測値)に対して、切換関数を次のように定義する。$$\sigma = c_1 e + c_2 \dot e + c_3 \int_0^t e(\tau) d\tau$$スライディングモード (\(\sigma = 0\)) が理想的に維持されると仮定すると、\(\dot \sigma =0\)でもあるため、 $$c_1 \dot e + c_2 \ddot e + c_3 e = 0$$整理すると、$$c_2 \ddot e + c_1 \dot e + c_3 e = 0$$ この2階の線形微分方程式が、スライディングモード中の偏差の動特性を表す。この特性方程式は、$$c_2 s^2 + c_1 s + c_3 = 0$$(\(s\) は微分演算子)であるので、この根(極)を適切に配置することで、偏差の収束特性(速応性、減衰性など)を調整できる。これは、周波数領域で偏差の動特性のボード線図などを所望の形に近づけること(周波数整形)に相当する。
・\(c_3\) (積分項の係数): これを導入することで、偏差の動特性に積分要素が入り、低周波ゲインが上昇します。これにより、ステップ状の外乱や指令値に対する定常偏差をゼロに近づける効果がある。
・\(c_1,\;c_2\) (比例項、微分項の係数):これらの係数を調整することで、偏差の動特性の固有振動数や減衰比を調整し、応答の速さやオーバーシュートの大きさを制御する。例えば、減衰比を上げることで振動を抑制し、固有振動数を上げることで応答を速くすることができる。
2次系の位置決め制御への適用
2次系の制御対象を式(1)とする。$$ \ddot y + a_1 \dot y + a_0 y = b_0 u + d(t) \;\;\; \cdots (1)$$ここで、\(y\)は出力(位置)、\(u\)は制御入力、\(d(t)\) は外乱である。\(a_1,\;a_0,\;b_0\)はシステムパラメータで既知とする。 状態変数として\( x_1=y,\; x_2= \dot y \)を選ぶと、状態方程式は、式(2)となる。$$ \dot x_1 = x_2 \\ \dot x_2 =−a_0 x_1 − a_1 x_2 + b_0 u + d(t) \;\;\; \cdots (2)$$出力\(y\)を指令値\(y_d(t)\)に追従させることを目的とする。偏差を\(e(t)=y_d(t)−y(t)\) と定義する。従って、$$ \dot e= \dot y_d − \dot y = \dot y_d − x_2, \quad \ddot e = \ddot y_d − \ddot y = \ddot y_d − \dot x_2$$となる。
偏差の動特性が望ましい特性を持つように、PID型の切換関数を次のように設計する。$$\sigma = c_1(\dot y_d - x_2) + c_0(y_d - x_1) + c_I \int_0^t (y_d(\tau) -x_1(\tau))d \tau$$ ただし、実用上は \(\sigma = \dot e + \alpha e + \beta z\) (ここで \(\dot z = e\))と定義することが多い。スライディングモード (\(\sigma = 0\)) では、$$\dot e + \alpha e + \beta \int_0^t e(\tau) d \tau =0 $$両辺を時間で微分すると(\(\sigma =\)を維持するためには \(\dot \sigma =0\) も必要)、\(\ddot e + \alpha \dot e + \beta e =0\)これがスライディングモードにおける偏差の動特性となる。この特性方程式は、\(s^2+\alpha s + \beta = 0\)なので、この根が、望ましい減衰比 \(\zeta_d\)と固有角周波数\(\omega_{nd}\) を持つように、\(\alpha=2 \zeta_{d} \omega_{nd} \)および \(\beta = \omega_{nd}^2 \)と選ぶことができる。これにより、偏差の収束応答が調整でき、周波数特性が整形される。
制御入力\(u\)は、等価制御入力\(u_{eq}\) とスイッチング入力\(u_{sw}\) の和として設計する。\(u = u_{eq} + u_{sw}\) まず、\(\dot \sigma = 0\)の条件から等価制御入力\(u_{eq}\)を求める。$$ \sigma = (\dot y_d − x_2 ) + \alpha (y_d − x_1)+\ \beta z \\ \dot \sigma = (\ddot y_d − \dot x_2) + \alpha(\dot y_d − x_2) + \beta(y_d − x_1) \\ \dot \sigma = \ddot y_d− (−a_0 x_1 − a_1 x_2 + b_0 u + d(t)) + \alpha(\dot y_d − x_2) + \beta(y_d−x_1)\\ \dot \sigma = \ddot y_d + a_0 x_1 + a_1 x_2 − b_0 u − d(t) + \alpha(\dot y_d − x_2) + \beta(y_d − x_1)$$ \(\dot \sigma = 0\) とおき、\(u = u_{eq}\) とすると(ただし、外乱 \(d(t)=0\) として設計する)、$$b_0 u_{eq} = \ddot y_d + a_0 x_1 + a_1 x_2 + \alpha(\dot y_d − x_2) + \beta(y_d − x_1) \\ u_{eq} = \frac{1}{b_0} (\ddot y_d + a_0 x_1 + a_1 x_2 + \alpha(\dot y_d − x_2) + \beta(y_d − x_1))$$
スイッチング入力 \(u_{sw}\) は、状態量を切換超平面に引き込み、拘束するために用いられる。チャタリングを抑制するために、符号関数の代わりに飽和関数 \(\text{sat}(\sigma/\Phi)\) を用いることが一般的である。$$u_{sw} = K\text{sat}(\sigma/\Phi) = K \begin{cases} \text{sgn}(\sigma) & if ∣\sigma∣> \Phi \\ \sigma/\Phi & if ∣\sigma∣≤ \Phi \end{cases}$$ ここで、\(K\)はスイッチングゲイン、\(\Phi\)は境界層の厚さである。\(K\)は外乱やモデル化誤差の上界よりも大きく選ぶ必要がある。
Pythonによるシミュレーション
2次システムのスライディングモード制御をPythonでシミュレーションする。
*シミュレーション設定
・システムパラメータ:\(a_1=1.0,\; a_0=1.0,\; b_0=1.0\)
・制御パラメータ : 望ましい偏差の動特性を \(s^2+2s+1=0\) (臨界制動、\(\omega_{nd}=1, \; \zeta_d=1\)) とすると、\(\alpha=2,\; \beta=1\)。
・スイッチング制御パラメータ:\(K=2.0,\; \Phi=0.05\)
・指令値:\(y_d(t)=1.0\) (ステップ入力) for \(t \ge 0\)
・外乱:\(d(t)=0.5\) for \(t \ge t_d\) (ステップ状外乱、 \(t_d=5 s\))
・初期状態:\(x_1(0)=y(0)=0,\; x_2(0)=\dot y(0)=0,\; z(0)=\int e d \tau∣_{t=0} =0\)
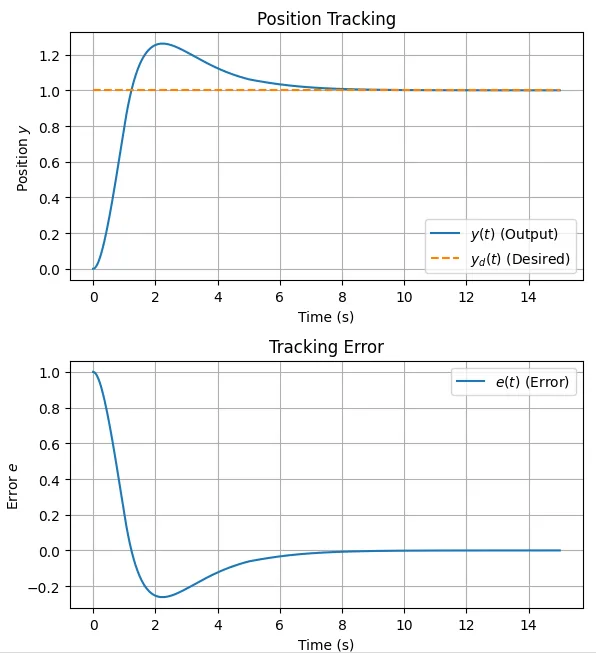
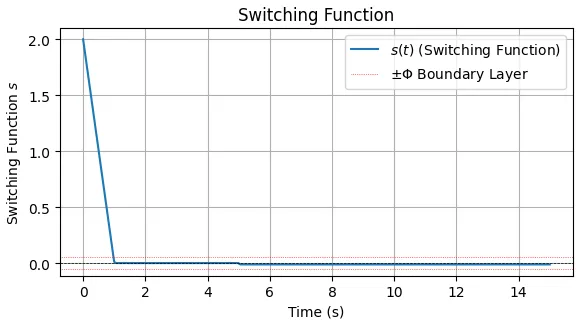
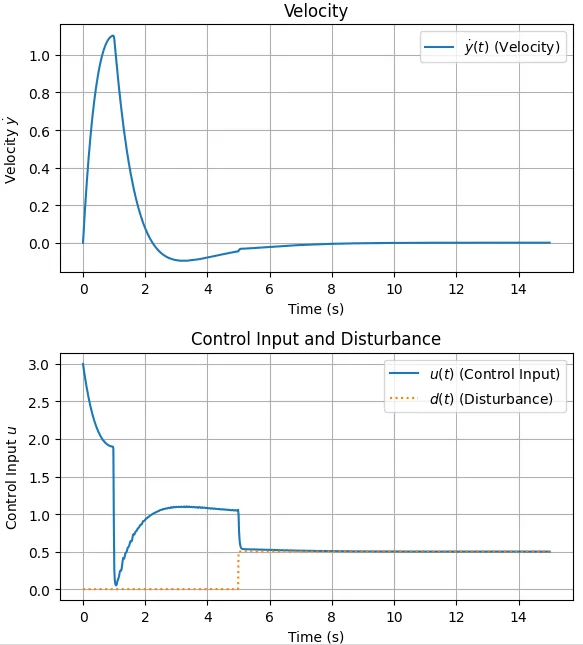
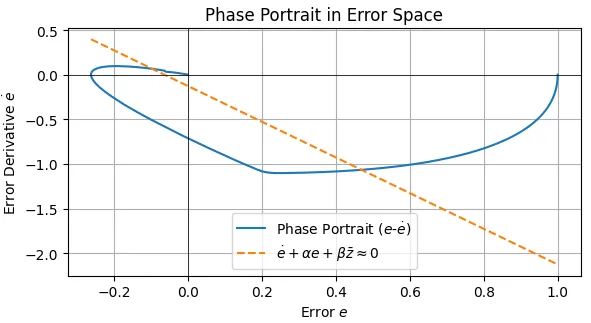
図1に位置と位置偏差の時間応答(ステップ応答)を示す。出力\(y(t)\)が目標値\(y_d(t) = 1.0\) に速やかに追従している。また、\(5\;s\)後に外乱\(d(t)\)が加わった後も目標値近傍に留まっている。偏差\(e(t)\)は速やかに0に収束し、外乱印加時にもその影響が抑制されている。特に、積分項(\(\beta\))の存在により、ステップ状の外乱や目標値に対する定常偏差が0に近づく。これが低周波ゲインを上げる周波数整形の一つの効果である。図2は、速度と制御入力の時間応答である。制御入力\(u(t)\)は、等価制御入力\(u_{eq}\)を中心に、スイッチング入力\(u_{sw}\)が重畳された形になる。飽和関数\(\text{sat}(s/\Phi)\)(記号\(\sigma\)の代わりに\(s\)を用いている)により、チャタリングは理想的な符号関数よりは抑制されている。また、外乱が加わったとき、それを打ち消すように制御入力が変化していることが分かる。図3より、切換関数\(s(t)\) は速やかに0近傍(境界層\(\pm \Phi\) 内)に到達し、その後もその中に留まることが期待される。これにより、システムがスライディングモードで動作していることが確認できる。図4は、偏差と偏差微分の位相平面図で、偏差\(e\)とその微分\(\dot e\)の軌跡が原点 \((0,\;0)\) に収束する様子が確認できる。また、\(s \approx 0\)の直線(実際には\(z\)も変動するため曲面)に沿って状態が収束していく様子が見られる。
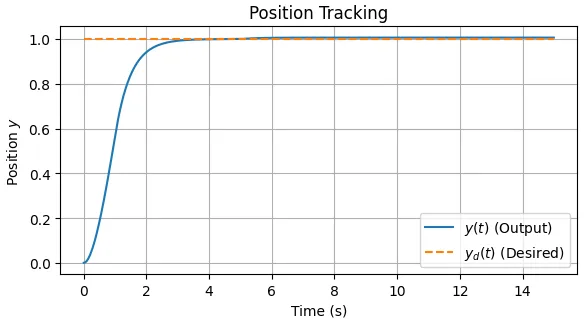
図5、図6は、積分項\(\beta = 0\)としたときのシミュレーション結果である。図5の位置の時間応答(ステップ応答)ではオーバーシュートは見られないが、ステップ状の外乱による定常偏差が見られる。位相平面図では、切換超平面(この場合は切換直線)に達してからは、切換超平面に拘束されて原点に向かっている様子が見られるが、原点からずれており、外乱により定常偏差が僅かに生じることが分かる。
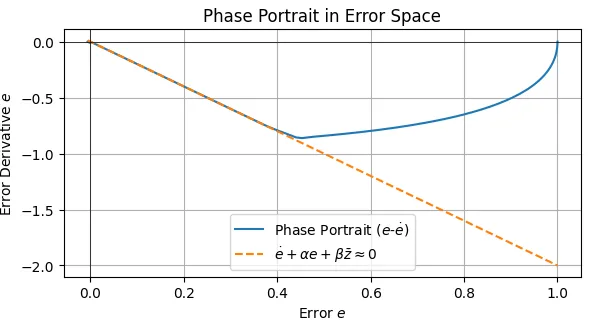
(\(\beta=0\))
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
# システムパラメータ
a1 = 1.0
a0 = 1.0
b0 = 1.0
# 制御パラメータ (エラーダイナミクス)
alpha = 2.0 # 2*zeta_d*omega_nd
beta = 1.0 # omega_nd^2
#beta = 0
# スイッチング制御パラメータ
K = 2.0 # スイッチングゲイン
Phi = 0.05 # 境界層の厚さ
# 目標値
def y_d_func(t):
return 1.0 if t >= 0 else 0.0
def y_d_dot_func(t): # 目標値の微分
return 0.0
def y_d_ddot_func(t): # 目標値の2階微分
return 0.0
# 外乱
def disturbance_func(t, t_d=5.0, d_mag=0.5):
return d_mag if t >= t_d else 0.0
# 飽和関数
def sat(s_val, phi_val):
if np.abs(s_val) > phi_val:
return np.sign(s_val)
else:
return s_val / phi_val
# システムの微分方程式
def system_dynamics(t, X):
x1, x2, z = X # y, y_dot, integral_of_e
# 目標値とその微分
y_d_val = y_d_func(t)
y_d_dot_val = y_d_dot_func(t)
y_d_ddot_val = y_d_ddot_func(t)
# 偏差とその微分
e_val = y_d_val - x1
e_dot_val = y_d_dot_val - x2
# 切換関数 s
s_val = e_dot_val + alpha * e_val + beta * z
# 等価制御入力 u_eq (外乱 d(t) は未知として設計)
u_eq = (1/b0) * (y_d_ddot_val + a0*x1 + a1*x2 + alpha*(y_d_dot_val - x2)
+ beta*(y_d_val - x1))
# スイッチング入力 u_sw
u_sw = K * sat(s_val, Phi)
# 全体制御入力
u_val = u_eq + u_sw
# 外乱
d_val = disturbance_func(t)
# 状態の微分
dx1_dt = x2
dx2_dt = -a0*x1 - a1*x2 + b0*u_val + d_val
dz_dt = e_val # de/dt ではなく e を積分
return [dx1_dt, dx2_dt, dz_dt]
# シミュレーション時間
t_start = 0
t_end = 15
t_span = [t_start, t_end]
t_eval = np.linspace(t_start, t_end, 1000)
# 初期状態 [y(0), y_dot(0), z(0)]
X0 = [0.0, 0.0, 0.0]
# シミュレーション実行
sol = solve_ivp(system_dynamics, t_span, X0, t_eval=t_eval, method='RK45')
# 結果の抽出
t = sol.t
x1_res = sol.y[0,:]
x2_res = sol.y[1,:]
z_res = sol.y[2,:]
# 目標値、偏差、制御入力、切換関数の再計算 (プロット用)
y_d_res = np.array([y_d_func(ti) for ti in t])
y_d_dot_res = np.array([y_d_dot_func(ti) for ti in t])
y_d_ddot_res = np.array([y_d_ddot_func(ti) for ti in t])
e_res = y_d_res - x1_res
e_dot_res = y_d_dot_res - x2_res
s_res = e_dot_res + alpha * e_res + beta * z_res
u_eq_res = (1/b0) * (y_d_ddot_res + a0*x1_res + a1*x2_res + alpha*
(y_d_dot_res - x2_res) + beta*(y_d_res - x1_res))
u_sw_res = np.array([K * sat(si, Phi) for si in s_res])
u_res = u_eq_res + u_sw_res
d_res = np.array([disturbance_func(ti) for ti in t])
# 結果のプロット
plt.figure(figsize=(12, 10))
plt.subplot(3, 2, 1)
plt.plot(t, x1_res, label='$y(t)$ (Output)')
plt.plot(t, y_d_res, label='$y_d(t)$ (Desired)', linestyle='--')
plt.xlabel('Time (s)')
plt.ylabel('Position $y$')
plt.title('Position Tracking')
plt.legend()
plt.grid(True)
plt.subplot(3, 2, 2)
plt.plot(t, x2_res, label='$\dot{y}(t)$ (Velocity)')
plt.xlabel('Time (s)')
plt.ylabel('Velocity $\dot{y}$')
plt.title('Velocity')
plt.legend()
plt.grid(True)
plt.subplot(3, 2, 3)
plt.plot(t, e_res, label='$e(t)$ (Error)')
plt.xlabel('Time (s)')
plt.ylabel('Error $e$')
plt.title('Tracking Error')
plt.legend()
plt.grid(True)
plt.subplot(3, 2, 4)
plt.plot(t, u_res, label='$u(t)$ (Control Input)')
plt.plot(t, d_res, label='$d(t)$ (Disturbance)', linestyle=':')
plt.xlabel('Time (s)')
plt.ylabel('Control Input $u$')
plt.title('Control Input and Disturbance')
plt.legend()
plt.grid(True)
plt.subplot(3, 2, 5)
plt.plot(t, s_res, label='$s(t)$ (Switching Function)')
plt.axhline(0, color='black', lw=0.5, linestyle='--')
plt.axhline(Phi, color='red', lw=0.5, linestyle=':', label=f'$\pm\Phi$ Boundary
Layer')
plt.axhline(-Phi, color='red', lw=0.5, linestyle=':')
plt.xlabel('Time (s)')
plt.ylabel('Switching Function $s$')
plt.title('Switching Function')
plt.legend()
plt.grid(True)
plt.subplot(3, 2, 6)
plt.plot(e_res, e_dot_res, label='Phase Portrait ($e$-$\dot{e}$)')
plt.xlabel('Error $e$')
plt.ylabel('Error Derivative $\dot{e}$')
plt.title('Phase Portrait in Error Space')
# Plot s=0 line for z=0 (approximation as z changes slowly initially)
# e_dot + alpha*e = 0 => e_dot = -alpha*e
e_for_s_line = np.linspace(np.min(e_res), np.max(e_res), 100)
# This is an approximation, as z is not always 0
# For better visualization, one might plot s=0 surface in 3D (e, e_dot, z)
# or project it. For simplicity, we show the e-e_dot plane.
plt.plot(e_for_s_line, -alpha*e_for_s_line -beta*np.mean(z_res), # mean(z) is a
rough approx.
label=r'$\dot{e} + \alpha e + \beta \bar{z} \approx 0$', linestyle='--')
plt.legend()
plt.axhline(0, color='black', lw=0.5)
plt.axvline(0, color='black', lw=0.5)
plt.grid(True)
plt.tight_layout()
plt.show()


