4. 種々の切換方式

スライディングモード制御において、実際にスライディング面上で使用される各種の切換方式（スイッチング方式）について、それぞれの特徴を整理する。

理想リレー切換方式

完全なON/OFF切換を行うリレー動作で、これまでの項目１．２．３．のシミュレーションで使用してきた切換方式である。
式で表すと、$$u(t) = \begin{cases} +K, & \sigma(x) > 0 \\ -K, & \sigma(x) < 0 \end{cases}$$ となる。
特徴をまとめると以下となる。
・鋭い切換により、理想的なスライディングモードが成立。
・状態はスライディング面に強制的に貼り付けられる。
・チャタリング（高周波振動）が発生しやすい。
・理論解析がしやすく、制御設計がシンプル。
このため、用途としては理論研究、理想的なシミュレーション、摩擦や遅れが小さい系への適用、となる。

理想的な飽和切換方式

状態がスライディング面近傍にあるとき、滑らかに出力を制限する切換方式である。
式で表すと、$$u(t) = \begin{cases} +K, & \sigma(x) > L \\ \frac{K}{L} \sigma(x), & |\sigma(x)| \leq L \\ -K, & \sigma(x) < -L \end{cases}$$となる。ここで \(L \gt 0\)は閾値である。
\(L \gt 0, \quad \pm L\)では、境界層に入るための境界を与える。境界層の外では、理想的なリレー切換特性に一致する。境界層内では、ハイゲインの線形制御となる。
特徴をまとめると以下となる。
・チャタリングが大幅に低減。
・スライディング面上では厳密な理想的スライディングモードではなく、近似スライディングモードになる。
・小さな閾値\(L\)を選べば高精度に近づけることも可能である。
・実システムにやさしい制御である。
用途としては、アクチュエータ制御、実機実装、電力エレクトロニクス系、などである。

ヒステリシス特性を持つリレー切換方式

リレー切換方式にヒステリシス（履歴）特性を加えたもので、実際のリレー動作に近い。
式で表すと、$$u(t) = \begin{cases} +K, & \sigma(x) > h \\ -K, & \sigma(x) < -h \\ \text{保持} & |\sigma(x)| \leq h \end{cases}$$である。ここで\(h \gt 0\)はヒステリシス幅である。\(2h \gt 0\)は\(\sigma\)に関するヒステリシスの量で、このヒステリシス特性は、スライディング面\(\sigma =0\)上で制御入力を切り換えることはない。このため、システムは定常状態でリミットサイクル（閉軌道）挙動となる。
特徴をまとめると以下となる。
・スイッチングの回数を減らすことで、チャタリングを防止する。
・スライディング面近傍で状態が小さく揺れるが、切換回数が制限される。
・厳密なスライディングモードではない。
この方式の用途は、スイッチング素子の寿命延長、摩耗抑制、機械系・パワーエレ系での利用が挙げられる。

切換方式の違いによる位相平面軌跡

切換方式の違いによる位相平面軌跡の特徴をシミュレーションにより図示する。対象となるシステムは、以下とする。$$\dot x = y, \quad \dot y = 2y -x +u, \quad u = -K x$$また、切換関数は、$$\sigma(x, y) = xS, \quad S = 0.5x + y$$とする。

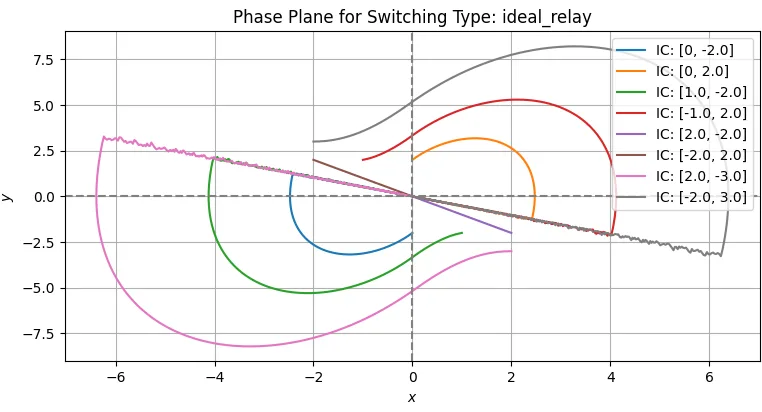
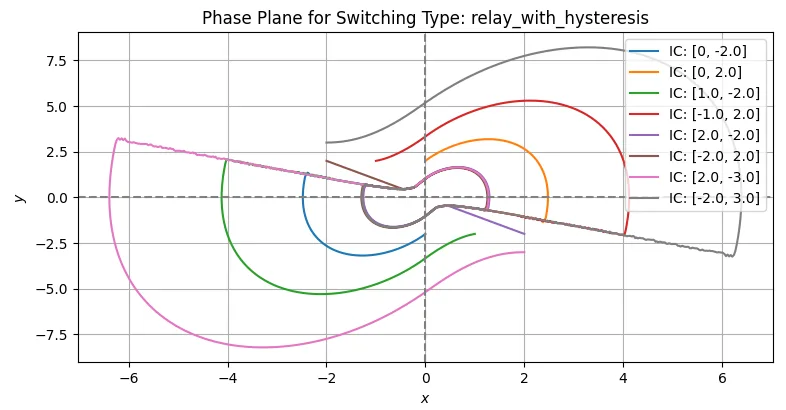
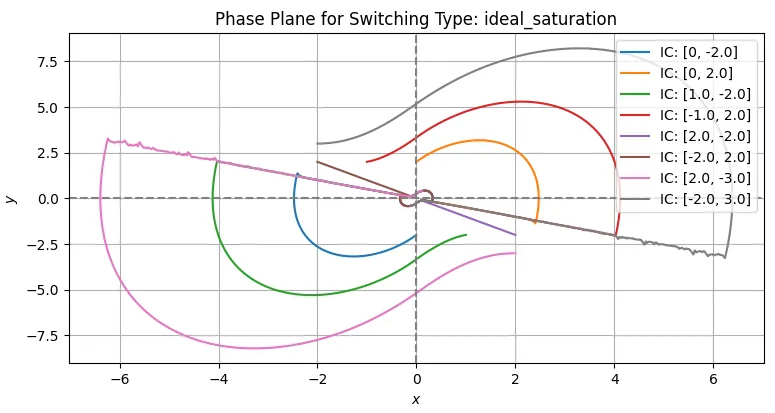
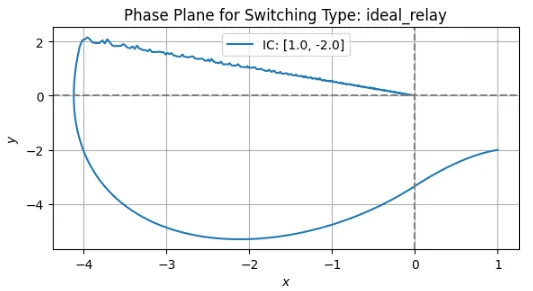
図１の理想リレー切換方式の場合、スライディングモードが理論通りに実現でき、初期値（IC）の\(x,y\)からスライディング面に到達して、スライディングモードで原点に達している。この切換方式を実装するには、制御対象の時定数より十分に短い時間での高速スイッチングが必要となる。制御対象が周波数帯域の低い機械システムや化学プラントであれば、現行のマイクロプロセッサで実装できる可能性が高い。ただし、スライディング面でのチャタリング（高周波振動）への対策が必要である。
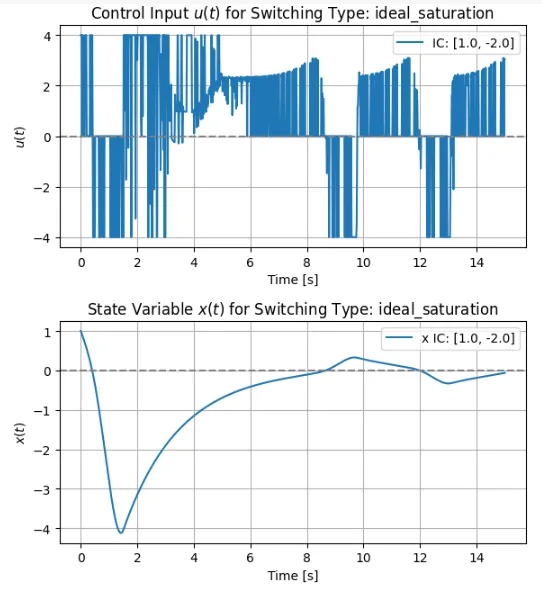
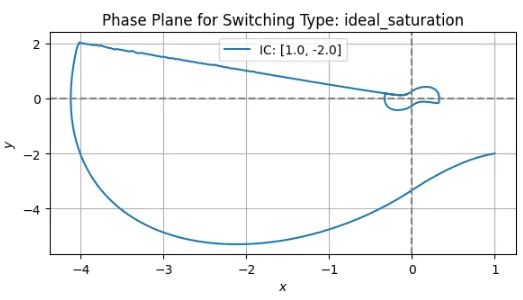
図２の飽和切換方式では、チャタリングを低減できるが、スライディング面上では厳密な理想的スライディングモードではなく、近似スライディングモードになる。図２では原点近傍でリミットサイクル（閉軌道）を生じているが、小さな閾値\(L\)を選べば精度良く原点に維持できる。
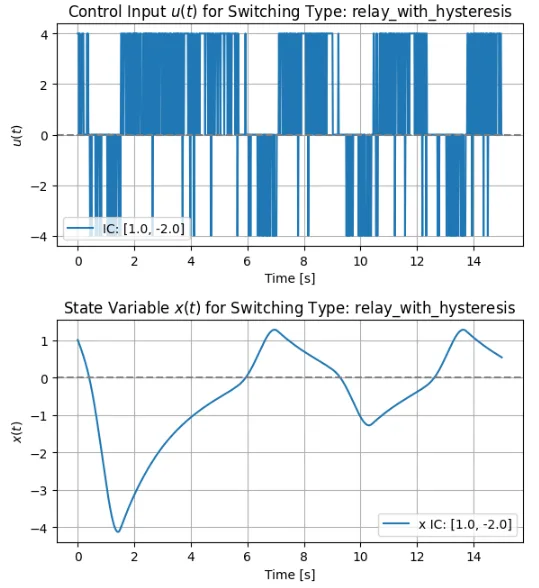
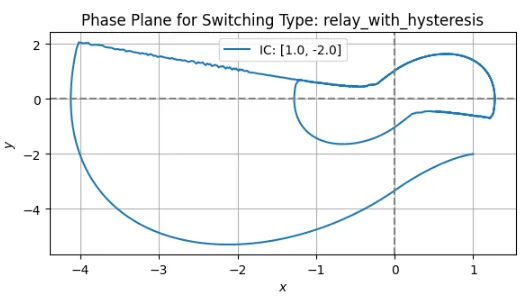
図３のヒステリシス特性を持つリレー切換方式では、スイッチングの回数を減らすことで、チャタリングを防止することができる。しかし、図３に示すように原点近傍でリミットサイクルに陥る可能性が高くなる。この場合、ヒステリシス特性のヒステリシス幅\(h\)を小さくすれば、リミットサイクルを描く軌道は小さくなるので、用途に応じて設定すればよい。

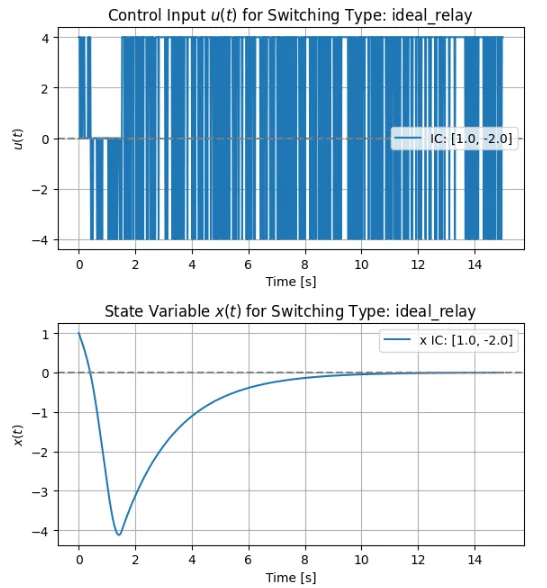
それぞれの切換方式での\(x\)及び\(u\)の時間応答特性と位相平面軌跡を示す。
初期値は、\([x,y] = [1.0, -2.0]\)としている。図６に示す飽和切換方式の場合、\(x\)は完全には０に収束していない。これは、閾値\(L\)を小さくすれば、問題ない範囲に収束させることが可能である。また、図８に示すヒステリシス特性を持つリレー切換方式の場合は、\(x\)は０に収束せず振動（リミットサイクル）していることがわかる。ヒステリシス幅\(h\)を小さくすれば、理想リレー切換方式に近づいて\(x\)は０に収束するが、当然ながら、実装可能性は低くなる。

※以下にPythonのスクリプトを示す。（＊図１のような位相面軌跡を表示する場合はIC（initial_conditions ）を変更すればよい。）

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# System parameters
K = 4.0  # Control gain
# Define the switching surface function
def sigma(x, y):
    S = 0.5 * x + y
    return x * S
# Define the equivalent control function (for each switching law)
def control_input(x, y, switching_type):
    sigma_val = sigma(x, y)
    if switching_type == "ideal_relay":
        return -K * np.sign(sigma_val)  # Ideal relay control
    elif switching_type == "ideal_saturation":
        L = 0.01
        if sigma_val > L:
          return -K
        elif sigma_val < -L:
          return K
        else:
          return  -K * sigma_val / L   # Ideal saturation control
    elif switching_type == "relay_with_hysteresis":
        h = 0.1  # Hysteresis width
        if sigma_val > h:
            return -K
        elif sigma_val < -h:
            return K
        else:
            return 0  # No control inside hysteresis range
# Define the system dynamics
def system_dynamics(t, state, switching_type):
    x, y = state
    u = control_input(x, y, switching_type)
    dxdt = y
    dydt = 2 * y - x + u * x
    return [dxdt, dydt], u
# Initial conditions
initial_conditions = [[1.0, -2.0]]
#initial_conditions = [[0, -2.0], [0, 2.0], [1.0, -2.0], [-1.0, 2.0],
#                      [2.0, -2.0], [-2.0, 2.0], [2.0, -3.0], [-2.0, 3.0]]
#
# Plot function for each switching type
def plot_sliding_surface_and_control(switching_type, initial_conditions):
    fig, axs = plt.subplots(3, 1, figsize=(6, 10))
    for initial_condition in initial_conditions:
        x0, y0 = initial_condition
        t_span = [0, 15]
        t_eval = np.linspace(0, 15, 1000)
        # Initialize u_list as an array with the same size as t_eval
        u_list = np.zeros_like(t_eval)
        def wrapped_dynamics(t, state):
            derivatives, u = system_dynamics(t, state, switching_type)
            # Find the closest index in t_eval to the current time t
            idx = np.abs(t_eval - t).argmin()
            u_list[idx] = u # Store u at the corresponding index in u_list
            return derivatives
        sol = solve_ivp(wrapped_dynamics, t_span, [x0, y0], t_eval=t_eval)
        x_vals = sol.y[0]
        y_vals = sol.y[1]
        # Phase plane plot
        axs[0].plot(x_vals, y_vals, label=f'IC: {initial_condition}')
        # Control input plot
        axs[1].plot(t_eval, u_list, label=f'IC: {initial_condition}')
        # x time response
        axs[2].plot(t_eval, x_vals, label=f'x IC: {initial_condition}')
    axs[0].set_xlabel(r'$x$')
    axs[0].set_ylabel(r'$y$')
    axs[0].set_title(f'Phase Plane for Switching Type: {switching_type}')
    axs[0].axhline(0, color='gray', linestyle='--')
    axs[0].axvline(0, color='gray', linestyle='--')
    axs[0].grid(True)
    axs[0].legend()
    axs[1].set_xlabel('Time [s]')
    axs[1].set_ylabel(r'$u(t)$')
    axs[1].set_title(f'Control Input $u(t)$ for Switching Type: {switching_type}')
    axs[1].axhline(0, color='gray', linestyle='--')
    axs[1].grid(True)
    axs[1].legend()
    axs[2].set_xlabel('Time [s]')
    axs[2].set_ylabel(r'$x(t)$')
    axs[2].set_title(f'State Variable $x(t)$ for Switching Type:
{switching_type}')
    axs[2].axhline(0, color='gray', linestyle='--')
    axs[2].grid(True)
    axs[2].legend()
    plt.tight_layout()
    plt.show()
# Now plot for each switching type
switching_types = ["ideal_relay", "ideal_saturation", "relay_with_hysteresis"]
for switching_type in switching_types:
    plot_sliding_surface_and_control(switching_type, initial_conditions)