1. ブール代数
ブール代数は、真理値「真」(1)と「偽」(0)の2つの値のみを扱う代数系である。論理を数学的に表現するために開発されたもので、ディジタル回路の設計や計算機の論理処理などに広く用いられている。
ディジタル回路:ディジタル回路は、0と1の2つの状態しか取り扱わない回路で、論理演算を行う回路であり、AND,OR,NOTの3つの基本要素だけで、様々な機能を実現する。
計算機:コンピュータは、論理演算によって計算を行うことができる。AND,OR,NOTなどの基本的な論理演算を組み合わせることで、複雑な計算を行う。
論理学:ブール代数は、論理学においても重要な役割を果たしている。論理学では、真理値の組み合わせによる論理演算を研究する。ブール代数は、論理学における論理演算を数学的に表現するために用いる。
以下、ブール代数のディジタル回路に関係する部分についてまとめる。
ブール代数の定義
集合\(L\)から与えられ、その任意の元\(A,\;B\)に対して2つの演算\(\cdot\)(AND:乗法)と\(+\)(OR:加法)が定義されるとき、\(A \cdot B\)、\(A+B\)は\(L\)の元であり、次の公理が成立する。
・交換則:\(A \cdot B = B \cdot A\)、 \(A+B=B+A\)
・結合則:\(A \cdot (B \cdot C) = (A \cdot B ) \cdot C\)、 \(A+(B+C)=(A+B)+C\)
・分配則:\(A \cdot (B+C) = (A \cdot B) +( A \cdot C)\)、 \(A + (B \cdot C) = (A + B) \cdot (A + C)\)
・吸収則:\(A + (A \cdot B) = A\)、 \(A \cdot (A + B) = A\)
・相補則:\(A \cdot \bar{A} = \emptyset\)、 \(A + \bar{A} = 1\)
典型的な例は、二つの元\(0,\;1\)のみの2点集合\(\{0 , \;1\}\)から成る場合である。これが現在のディジタルコンピュータの動作原理となっている。この場合、
乗法(AND):\(0 \cdot 0 = 0, \;\;\;\; 0 \cdot 1 = 0, \;\;\;\; 1 \cdot 0 = 0,\;\;\;\; 1 \cdot 1 =1\)
加法(OR):\(0 + 0 =0 , \;\;\;\; 0 + 1 = 1,\;\;\;\; 1 + 0 =1,\;\;\;\; 1 +1 =1\)
また、\(A=\{1,\;0\}\)とすると、$$A \cdot 0 = 0 \;\;\;\;\;\; A + 0=A \;\;\;\;\; A + 1 =1 \\ A \cdot \bar{A} = 0 \;\;\;\;\; A \cdot A = A \;\;\;\;\; A + \bar{A} = 1 \;\;\;\;\; A + A = A$$と表せる。ただし、\(\bar{A}\)は\(A\)の補元とする。(\(\bar{0}=1, \;\;\;\; \bar{1} =0\))
AND回路、OR回路
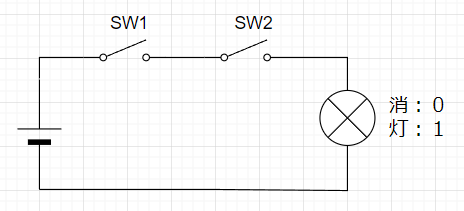
図1は「ON/OFF 基本回路」例である。スイッチ(SW)の閉をON、開をOFFとし、ON状態を1、OFF状態を0に対応させる。この時、ONでライトが点灯し、OFFでライトが消灯するので、点灯を1、消灯を0に対応させる。
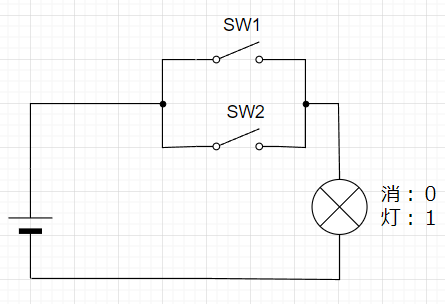
図1の基本回路を基にして、図2のようにSWを直列に接続すると、表1の動作、ANDとなる。
| SW1 | SW2 | Light |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
(AND回路の動作)
図1の基本回路を基にして、図3のようにSWを並列に接続すると、表2の動作、ORとなる。
| SW1 | SW2 | Light |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
(OR回路の動作)

命題、論理変数
真(true:1)、偽(false:0)が明確な文章を命題という。
命題を記号\(A,B,C,D,\cdots\)という変数(論理変数)で表し、命題が真のとき1,偽のとき0という記号で表す。論理変数を含んだ式を論理式(論理関数)という。
論理変数とは、真理値(真または偽)をとる変数で、論理変数は、論理回路やプログラミング言語でよく使用される。論理変数は、通常、大文字のアルファベットで表す。論理変数の真理値は、通常、1 または 0 で表されます。1 は真を表し、0 は偽を表す。
論理変数は、論理演算によって他の論理変数の真理値を計算することができる。論理演算には、AND、OR、NOT などがある。AND 演算は、2 つの論理変数の真理値がどちらも真である場合にのみ、真の値を返し、OR 演算は、2 つの論理変数の真理値のうちどちらか一方が真である場合に、真の値を返す。NOT 演算は、論理変数の真理値を反転する。
論理演算の例
$$(A + \bar{B} + C + \bar{D})\cdot C = A \cdot C + \bar{B} \cdot C + C \cdot C + \bar{D} \cdot C \\= C \cdot A + C \cdot \bar{B} + C + C \cdot \bar{D} \\ = C \cdot A + C \cdot \bar{B} + C \cdot(1 + \bar{D}) \\= C \cdot A + C \cdot \bar{B} + C \\= C \cdot A + C \cdot( \bar{B} + 1) \\= C \cdot A + C\\= C \cdot(A + 1)=C$$
$$(A + B)\cdot (A + C ) = A \cdot A + A \cdot C + B \cdot A + B \cdot C \\= A + A \cdot C + B \cdot A + B \cdot C \\=A \cdot(1 +C ) + B \cdot A + B \cdot C \\= A + B \cdot A + B \cdot C \\= A \cdot (1 + B) + B \cdot C \\= A + B \cdot C$$

