7. トランジスタの静特性

BJTの静特性

BJT（バイポーラトランジスタ）の静特性とは、トランジスタ単体の端子間に所定の電圧を加えた状態での電流の流れ方を示す特性である。BJTは非線形素子であるため、BJTの端子間に電圧を加えたときに流れる電流は、必ずしも電圧に比例しない。この電圧と電流の関係をグラフにしたものをBJTの静特性曲線という。
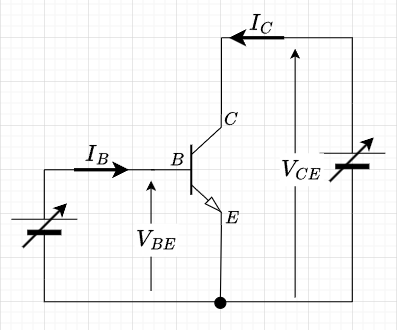
図１はBJTの静特性測定回路例である。例えば、$V_{CE} - I_C$特性の測定では、ベース電流$I_B$を一定として、$V_{CE}$を変化させたときのコレクタ電流$I_C$を測定する。
図２はBJTの静特性例（2SC1815）である。2SC1815は最大コレクタ電流（$I_C\;{max}$）150mAの小信号用トランジスタである。図２の各特性は以下となる。

・$I_B-V_{BE}$特性（入力特性：図2の第3象限）：入力特性は、コレクタ-エミッタ間電圧$V_{CE}$を一定とした時に、ベース-エミッタ間電圧$V_{BE}$とベース電流$I_B$の関係を表した特性である。
この特性の傾きは、入力インピーダンス$h_{ie} \;[\Omega]$を表している。 $$h_{ie}=\frac{\Delta V_{BE}}{\Delta I_B}=\frac{v_{be}}{i_b} \; [\Omega]$$ 入力特性は、BJTの動作領域を示すために用いる。

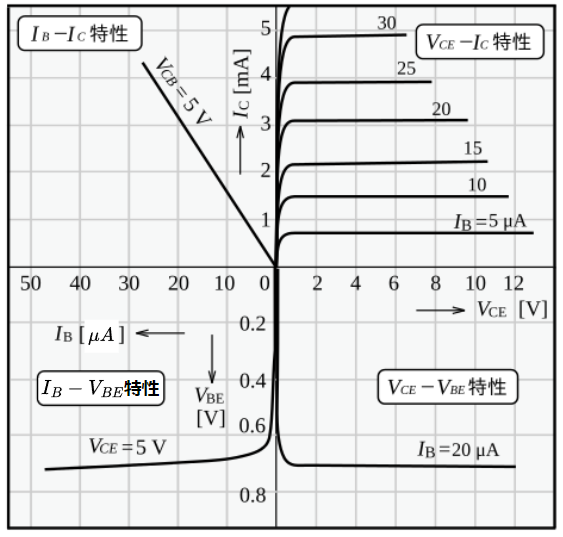
・$V_{CE}-I_C$特性（出力特性：図2の第1象限）：出力特性は、ベース電流$I_B$を一定とした時に、コレクタ-エミッタ間電圧$V_{CE}$とコレクタ電流$I_C$の関係を表した特性である。$V_{CE}$ が０から少し大きくなると$I_C$が急激に大きくなるが、$V_{CE}$が１V以上になると、$V_{CE}$を変化させても$I_C$はほとんど変化しない。
この特性の傾きは、出力アドミタンス$h_{oe} \;[S]$を表している。 $$h_{oe} = \frac{\Delta I_C}{\Delta V_{CE}} = \frac{i_c}{v_{ce}} \; [S]$$ アドミタンスは、電流の流れやすさを表しており、インピーダンスの逆数である。従って、出力インピーダンス$Z_o$は、 $$Z_o =\frac{1}{h_{oe}} \; [\Omega]$$ である。
出力特性は、バイポーラトランジスタの増幅特性を示すために用いられる。

・$I_B-I_C$特性（電流伝達特性：図2の第2象限）：電流伝達特性は、$V_{CE}$を一定に保ち、ベース電流$I_B$の変化に対するコレクタ電流$I_C$の変化を測定したもので、これはほぼ比例関係にあり直線で表せる。
この特性の傾きは、電流増幅率$h_{fe} (=\beta)$を表している。 $$h_{fe}=\frac{\Delta I_C}{\Delta I_B}=\frac{i_c}{i_b}=\beta$$ 図2第2象限の単位を見てわかるように、ベース電流$I_B$は$[\mu A]$、コレクタ電流$I_C$は$[mA]$となっており、小さな入力電流$I_B$に対して、大きな出力電流$I_C$となり、電流の増幅作用があることがわかる。

・$V_{CE}-V_{BE}$特性（電圧帰還率：図2の第4象限）：ベース電流$I_B$を一定にして、コレクタ・エミッタ間電圧$V_{CE}$の変化に対するベース・エミッタ間電圧$V_{BE}$を測定した特性である。
この特性の傾きは、電圧帰還率$h_{re}$を表している。 $$h_{re}=\frac{\Delta V_{BE}}{\Delta V_{CE}}=\frac{v_{be}}{v_{ce}}$$ この値は非常に小さい。

BJTの静特性は、以下の3つの領域に分けられる。
１）遮断領域：コレクタ-エミッタ間電圧$V_{CE}$が十分に大きい場合、ベース電流$I_B$がいくら大きくてもコレクタ電流$I_C$は流れない。この領域を遮断領域と呼ぶ。
２）活性領域：コレクタ-エミッタ間電圧$V_{CE}$が小さい場合、ベース電流$I_B$の増加に伴ってコレクタ電流$I_C$も増加する。この領域を活性領域と呼ぶ。BJTの増幅特性は、この領域で利用する。
３）飽和領域：コレクタ-エミッタ間電圧$V_{CE}$が十分に小さい場合、コレクタ電流$I_C$はベース電流$I_B$の増加に比例しなくなる。この領域を飽和領域と呼ぶ。BJTをスイッチとして用いるときは、この領域を利用する。