11. コンデンサの構造と性質
電荷の性質
電荷は物質が持つ最も基本的な性質の一つであり、正か負の値をとる。電荷が正の場合はプラス(\(+\))の符号で表され、電荷が負の場合はマイナス(\(-\))の符号で表される。
電荷は、同じ符号の電荷は反発し、異なる符号の電荷は引き合う。また、電荷は量子化された量であり、物理学の基本定数である素電荷を持つ電子が最小単位となる。
物質中には、電子や陽子といった荷電粒子が存在し、これらの荷電粒子が相互作用することによって物質の性質が決まる。電荷は、物質中の粒子同士の相互作用や、電場や磁場の影響を受けることで、物理現象の多くを説明するために重要な役割を果たす。
電荷の正負
正電荷(+)と負電荷(-)があり、それぞれ単独に存在することができる。
静電力は、
同種の電荷間(+と+,-と-)には反発力、
異種の電荷間(+と-)には吸引力が働く。
+電荷と-電荷が一緒になると、電気を帯びていない状態(電気的中性)となる。
金属の構造(原子模型)
金属中に存在する自由電子は、金属イオンが共有する電子の中で、外側の電子であり、原子核に強く束縛されていない電子のことを指す。
金属の原子は、一般的に、外側の電子(最外殻電子)を共有することで化学結合を形成する。しかし、金属中では、金属イオン同士が共有する電子が存在し、それが自由電子として金属内部を自由に移動できる。自由電子は、金属中の陽イオンの間を自由に移動できるため、金属イオン間に働く電気力によって金属結合を形成する。
自由電子は、金属中の性質に大きく影響を与える。例えば、自由電子は金属中を自由に移動できるため、金属は電気を通すことができる。
自由電子の量は金属の種類や状態によって異なり、自由電子の数が多い金属ほど導電性や熱伝導性が高くなる傾向がある。
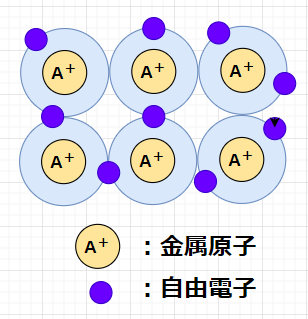
金属の原子模型
金属の原子模型は、原子核(+電荷)と原子核に束縛された電子(-電荷) と 自由電子(-電荷)からなる。
コンデンサ(キャパシタ)
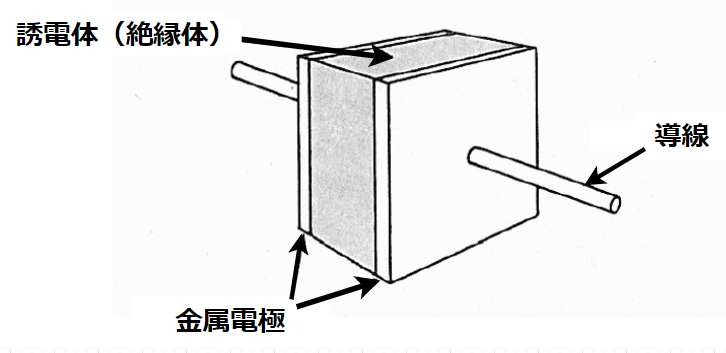
コンデンサは、2つの導体間に誘電体(絶縁体)を挟んだ電気素子である。一般的に、コンデンサは平板状の電極をもつ構造である。
コンデンサは、2つの平板状の導体で構成され、これらの導体は互いに平行に配置され、固定された距離で保持される。この2つの導体の間には、通常、空気、紙、プラスチックなどの誘電体が挿入される。
キャパシタの導体は、一般的に金属箔、金属メッシュ、または導電性塗料で作られており、誘電体は、紙、プラスチック、ガラス、セラミックなど、様々な素材で作られている。誘電体の選択は、コンデンサの容量、使用条件、および電気的特性に応じて選択される。
コンデンサは、2つの導体間に蓄積された電荷を保持するために使用される。電気エネルギーを蓄積し、放電することができるため、電源フィルタリング、信号処理、電源回路、電気モータ制御など、多くのアプリケーションで使用される。
コンデンサ、キャパシタ
「コンデンサ」の語源は、ラテン語の「condēnsāre」に由来する。物質をより密度の高い状態に変えるプロセス、濃縮することを指す。コンデンサは、電気エネルギーを蓄積することでエネルギーを密度の高い状態に保持する素子であることから、この名前が付けられた。なお、コンデンサは、英語圏ではキャパシタ「Capacitor」とも呼ばれる。これは、この素子が「電気容量」(英語で「capacity(容量)」)を持っていることを示す言葉から来ている。
コンデンサの動作
電圧を加えていないときは、両極板共に、 +電荷と-電荷が同数あるので 、電気的中性 の状態である。
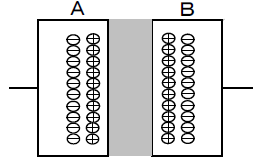
極板Aに+、 極板Bに-となる ように電源電圧を印加したとき極板Aの電子が電源の+の方に吸いつけられ、 電源の-から極板Bに電子が移動する。(回路に電流が流れるこれにより、 極板Aでは電子が少なくなるので正に帯電し、極板Bでは電子が多くなるので負に帯電 することになる。この結果、 A-B間に電位差\(V_{AB}\) を生じる。
【極板A(正に帯電)の方が電位が高い】
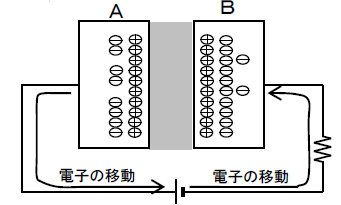
「A-B間の電位差=電源の起電力」となると、電子の移動は停止する。(回路の電流= 0 となる。)
コンデンサは、 極板Aに+電荷,極板Bに-電 荷を蓄えていると解釈してもよい。(コンデンサは充電された という)極板Aの電荷を\(+Q\) とすると、極板Bの電荷は\(-Q\) となる。(両電極の電荷量の絶対値は等しい)このとき、【コンデンサは電荷 \(Q\) を蓄えている】 という。
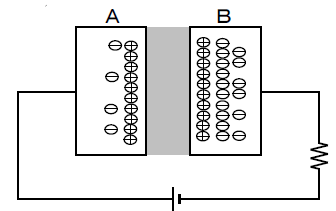
充電された状態で電源を切り離すと、 コンデンは充電されたままとなる。の状態は長時間保存される。 一時的な電池となる。
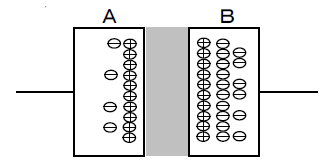
充電されたコンデンサを短絡すると、 極板Bに過剰にある電子が 、抵抗を通って極板Aに移動するので 、極板Bの電子は徐々に減少する。 これを 放電 という。電子が移動するので電流が流れる。放電が始まると 、A-B間の電位差は減少する。極板Bの電子が減少して図2の状態になると電子の移動は停止する。このとき 、A-B間の電位差= 0V となる。(完全放電充電されたコンデンサは一時的な電池と同じ働きをする。
(負荷に電流を流そうとする能力がある)
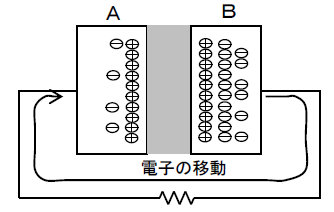
静電容量(キャパシタンス)
静電容量とは、2つの導体の間に存在する電気的なポテンシャル差に対して、その導体間に蓄えられる電荷量の比を表す物理量である。すなわち、静電容量は、電荷を蓄える性質を示す指標である。
静電容量は、導体の形状や大きさ、導体間の距離、媒質の誘電率によって決まる。一般的に、導体間の距離が狭く、導体の面積が広いほど、静電容量は大きくなる。また、媒質の誘電率が高い場合にも、静電容量は大きくなる。
静電容量(キャパシタンス: Capacitance)は、\(V\; [V]\)印加したときに蓄積される電荷量を\(Q \; [C] \) (クーロン)とすると、このコンデンサの静電容量C は、$$C = \frac{Q}{V}$$ と表される。Cの単位:\(F\)(ファラッド)
【例】 \(1 \; \mu F = 1 \times 10^{-6} \; F\) \(1 \; pF = 1 \times 10^{-6} \; \mu F = 1 \times 10^{-12} \; F\)
コンデンサの直列接続
2個のコンデンサ(\(C_1\),\(C_2\))を直列接続したものに抵抗を介して電源を接続する。
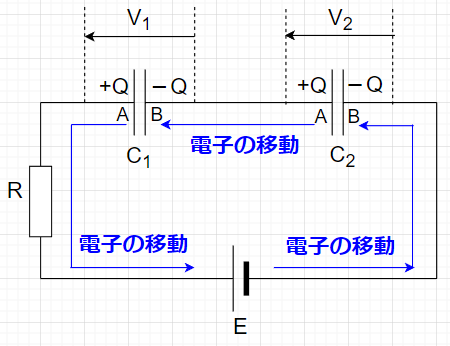
1)コンデンサ\(C_1\) の極板Aの電子が電源を通ってコンデンサ\(C_2\) の極板Bに移動する。この結果、コンデンサ\(C_1\) の極板Aは正に帯電し、コンデンサ\(C_2\)の極板Bは負に帯電する。
2)コンデンサ\(C_2\) の極板Aの電子は、コンデンサ\(C_1\) の極板Aの正電荷に引き寄せられて、コンデンサ\(C_1\) の極板Bに移動する。
この結果、コンデンサ\(C_2\) の極板Aは正に帯電し、コンデンサ\(C_1\) の極板Bは負に帯電する。
3)それぞれのコンデンサに電位差を生じる。\(V_1 + V_2 =E\)となると、電子の移動は停止する。(充電終了)
4)コンデンサ\(C_1\) に蓄えられた電荷量\(=Q\)、コンデンサ\(C_2\) に蓄えられた電荷量\(=Q\)
電源がコンデンサ群に充電した電荷量\(=Q\)となる。
注意)直列接続されたコンデンサ\(C_1\),\(C_2\) の電荷は常に同一である。
充電が終了したときの状態(回路には電流が流れていない)において、電源\(E\)から見た直列接続されたコンデンサ群の静電容量を\(C_s\)とすると、$$E = V_1 + V_2 \\ E = \frac{Q}{C_s} \\ V_1 = \frac{Q}{C_1} \\ V_2 = \frac{Q}{C_2}$$これより、$$\frac{Q}{C_s} = \frac{Q}{C_1} + \frac{Q}{C_2}$$となるので、$$\frac{1}{C_s} =\frac{1}{C_1} +\frac{1}{C_2}$$を得る。以上より、コンデンサ\(C_1\)、\(C_2\)の直列接続の合成静電容量\(C_s\)は、$$C_s= \frac{1}{\frac{1}{C_1} +\frac{1}{C_2}}$$と表せる。
コンデンサの並列接続
2個のコンデンサ(\(C_ 1\), \(C_ 2\) )を並列接続したものに 抵抗を介して電源を接続する。
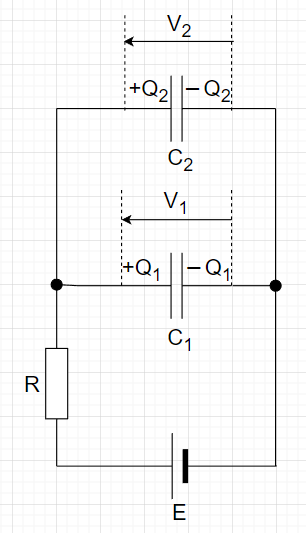
1)電源\(E\)によって\(C_1\),\(C_2\) の極板の電子が移動して、 \(C_1\),\(C_2\) に電荷が蓄積される。
2)\(C_1\)と\(C_2\) には常に同一の電圧が加わる。$$V_1=V_2=E \cdots (1)$$
となると、電荷の移動が停止する(充電終了)。
3)電源から供給された電荷量を\(Q_p\) ,コンデンサ\(C_1\),\(C_2\) に蓄えられた電荷量を\(Q_1\),\(Q_2\)とすると、$$Q_p = Q_1 + Q_2 \cdots (2)$$
4)電源からみた並列接続されたコンデンサ群の静電容量を\(C_p\)とすると、$$Q_p = C_p \cdot E$$である。また、$$Q_1 = C_1\cdot E \\ Q_2 = C_2 \cdot E$$である。これらを(2)式に代入すると、$$C_p \cdot E = C_1 \cdot E + C_2 \cdot E \\ (C_1 + C_2) \cdot E$$これより、コンデンサ\(C_1\),\(C_2\)の並列合成静電容量\(C_p\)は、$$C_p = C_1 + C_2$$と表される。


“11. コンデンサの構造と性質” に対して2件のコメントがあります。
コメントは受け付けていません。