14. 二次遅れ要素（２次遅れ系）の時間応答

二次遅れ要素（2次遅れ系）の伝達関数は分母が\(s\)に関して二次式となる。\(K\)はゲイン定数、\(\zeta\)は減衰係数、\(\omega_{n}\)は固有振動数（固有角周波数）と呼ばれ、伝達関数の特徴を決める定数である。二次遅れ要素は入力の周波数が高くなるほど出力の位相を遅れさせる特性を持っている。なお、位相の変化は、0°～-180°の範囲である。

＊二次遅れ要素（2次遅れ系）
$$G(s)=\frac{K{\omega_n}^2}{s^2+2\zeta\omega_ns+{\omega_n}^2}$$ (以降、\(K=1\)としたときの標準形で考える。）
$$G(s)=\frac{{\omega_n}^2}{s^2+2\zeta\omega_ns+{\omega_n}^2}$$
・単位インパルス応答
\(g(t)=\mathcal{L}^{-1}\{G(s)\}\)
ここで、特性方程式\(s^2+2\zeta\omega_ns+{\omega_n}^2=0\)の根（伝達関数の極）によって、逆ラプラス変換は３通りに分かれる。
つまり、特性方程式の2根は、$$p_1,p_2=-\omega_n\zeta\pm\omega_n\sqrt{\zeta^2-1}$$ なので、以下のようになる。
１）\(\zeta>1\)のとき負の実数根
2根は、$$p_1=-\omega_n(\zeta-\sqrt{\zeta^2-1}),$$ $$p_2=-\omega_n(\zeta+\sqrt{\zeta^2-1})$$と相異なる負の実数根となる。従って、インパルス応答\(g(t)\)は次のようになる。
$$g(t)=\mathcal{L}^{-1}\left\{ \frac{{\omega_n}^2}{(s-p_1)(s-p_2)}\right\}$$ $$=\mathcal{L}^{-1}\left\{\frac{A_1}{s-p_1}+\frac{A_2}{s-p_2}\right\}$$ $$=A_1e^{p_1t}+A_2e^{p_2t}$$ \(A_1,A_2\)は、部分分数展開したときの係数で正の実数となる。\(p_1,p_2\)は負の実数なので、\(g(t)\)は非振動的に減衰し０に収束する。このとき\(\left|p_1\right|,\left|p_2\right|\)が大きいほど速く０に収束することが分かる。

２）\(\zeta=1\)のとき負の実数重根
重根は、\(p_1=p_2=-\omega_n\)となる。このときインパルス応答\(g(t)\)は次のようになる。
$$g(t)=\mathcal{L}^{-1}\left\{\frac{{\omega_n}^2}{(s+\omega_n)^2}\right\}$$ $$={\omega_n}^2te^{-\omega_nt}$$ \(\omega_n\)は正の実数なので\(g(t)\)は非振動的に減衰し０に収束する。

３）\(0\le\zeta<1\)のとき複素共役根（実部は負）
\(\zeta^2-1<0\)となるので、2根は複素共役根$$p_1=-\omega_n(\zeta-j\sqrt{1-\zeta^2}),$$ $$p_2=-\omega_n(\zeta+j\sqrt{1-\zeta^2}) $$となる。このときインパルス応答\(g(t)\)は次のようになる。
$$g(t)=\mathcal{L}^{-1}\left\{\frac{{\omega_n}^2}{(s-p_1)(s-p_2)}\right\}$$ $$=\frac{\omega_n}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_nt}\sin{\sqrt{1-\zeta^2}\omega_nt}$$ \(\zeta=0\)のときは、単振動（\(\omega_n\sin{\omega_n}t\)）となる。
※詳細な誘導は参考文献やこちらのサイトを参考にして欲しい。

・単位ステップ応答
\(y(t)=\mathcal{L}^{-1}\{G(s)U(s)\}\)ここで、\(U(s)\)は単位ステップ関数のラプラス変換なので、\(U(s)=1/s\)である。
単位インパルス応答と同様に、二次遅れ要素\(G(s)\)の特性方程式\(s^2+2\zeta\omega_ns+{\omega_n}^2=0\)の根（伝達関数の極）によって、逆ラプラス変換は３通りに分かれる。導出の詳細は参考文献を参照してほしい。ここでは結果のみ示す。
１）\(\zeta>1\)のとき負の実数根
2根は、$$p_1=-\omega_n(\zeta-\sqrt{\zeta^2-1}),$$ $$p_2=-\omega_n(\zeta+\sqrt{\zeta^2-1})$$と相異なる負の実数根となる。従って、単位ステップ応答\(y(t)\)は次のようになる。
$$y(t)=\mathcal{L}^{-1}\left\{ \frac{{\omega_n}^2}{(s-p_1)(s-p_2)}\cdot\frac{1}{s}\right\}$$ $$=\mathcal{L}^{-1}\left\{\frac{B_1}{s}+\frac{B_2}{s-p_1}+\frac{B_3}{s-p_2}\right\}$$ $$=B_1+B_2e^{p_1t}+B_3e^{p_2t}$$ $$=1-\frac{\sqrt{\zeta^2-1}+\zeta}{2\sqrt{\zeta^2-1}}e^{p_1t}-\frac{\sqrt{\zeta^2-1}-\zeta}{2\sqrt{\zeta^2-1}}e^{p_2t}$$となり、\(p_1,p_2\)は負の実数なので非振動的に１（ステップ入力の１）に収束する。

２）\(\zeta=1\)のとき負の実数重根
重根は、\(p_1=p_2=-\omega_n\)となる。このとき単位ステップ応答\(y(t)\)は次のようになる。
$$y(t)=\mathcal{L}^{-1}\left\{\frac{{\omega_n}^2}{(s+\omega_n)^2}\cdot\frac{1}{s}\right\}$$ $$=1-(1+\omega_nt)e^{-\omega_nt}$$ \(\omega_n\)は正の実数なので\(y(t)\)は非振動的1に収束する。

３）\(0\le\zeta<1\)のとき複素共役根（実部は負）
\(\zeta^2-1<0\)となるので、2根は複素共役根$$p_1=-\omega_n(\zeta-j\sqrt{1-\zeta^2}),$$ $$p_2=-\omega_n(\zeta+j\sqrt{1-\zeta^2}) $$となる。このとき単位ステップ応答\(y(t)\)は次のようになる。
$$y(t)=\mathcal{L}^{-1}\left\{\frac{{\omega_n}^2}{(s-p_1)(s-p_2)}\cdot\frac{1}{s}\right\}$$ $$=1-\frac{1}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_nt}\sin\left({\sqrt{1-\zeta^2}\omega_nt+\phi}\right)$$ ここで、$$\phi=\tan^{-1}\left(\frac{\sqrt{1-\zeta^2}}{\zeta}\right)$$となる。\(0\lt\zeta<1\)のとき、\(y(t)\)は振動しながら1に収束する。\(\zeta=0\)のときは、$$y(t)=1-\sin\left(\omega_nt+\frac{\pi}{2}\right)$$ $$=1-\cos\omega_nt$$となり、自然角周波数\(\omega_n\)での持続振動となる。

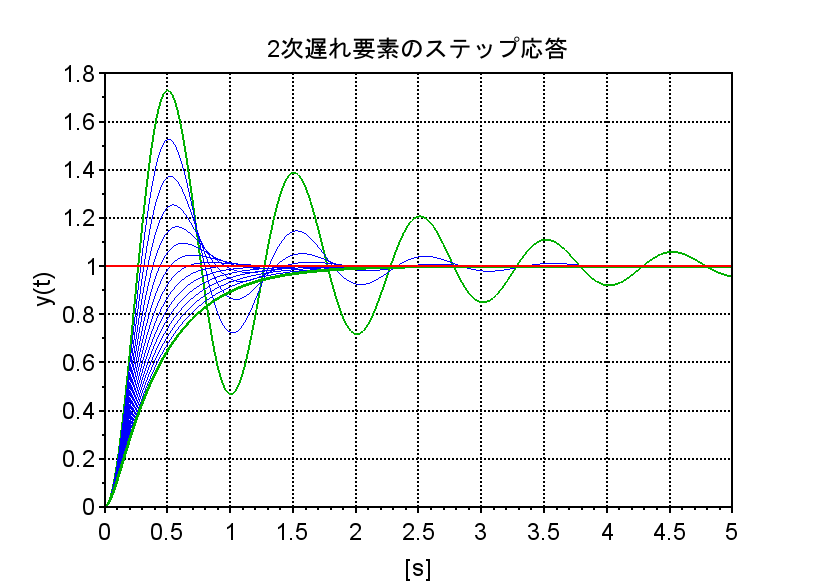
図は2次遅れ要素で自然角周波数\(\omega_n=2\pi f_n\),（自然周波数 \(f_n =1\) Hz ）としたときのステップ応答で、減衰係数\(\zeta=0.1\)のとき、大きく振動しながら１に収束している（\(y(t)=1.7\)に達している緑の線）。\(\zeta\)が大きくなるにしたがって振動が小さくなり、\(\zeta\ge1.0\)で非振動的に１に収束している。また、図では\(\zeta=1.5\)で最も緩やかに１に収束していることが分かる。なお、自然角周波数\(\omega_n\)は振動している場合は振動周期に、非振動的な場合は立ち上がりの速さに関係している。

Scilabによる二次遅れ要素の解析（ステップ応答）